考点与命题趋向分析
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
二、考点与命题趋向分析
(一)能力
1.理解圆及其有关概念,了解弧、弦、圆心角的关系,探索并了解点与圆、直线与圆以及圆与圆的位置关系.
2.探索圆的性质,了解圆周角与圆心角的关系、直径所对圆周角的特征.
3.了解三角形的内心和外心.
4.了解切线的概念,探索切线与过切点的半径之间的关系;能判定一条直线是否为圆的切线,会过圆上一点画圆的切线.
5.会计算弧长及扇形的面积,会计算圆锥的侧面积和全面积.
(二)命题趋向分析
1.今后的中考试题将更侧重在于具体问题中考查圆的定义及点与圆的位置关系,应在学习中侧重于如何运用如何解决实际问题.
【例1】由于过渡采伐森林和破坏植被,使我国某些地区多次受到沙尘暴的侵袭.近日A市气象局测得沙尘暴中心在A市正东方向400km的B处,正在向西北方向转移(如图所示),距沙尘暴中心300km的范围内将受其影响,问A市是否会受到这次沙尘暴的影响?
【分析】过点A作AC⊥BD交BD于点C,由题意可知沙尘暴中心正沿BD方向移动,当它移动到点C时,沙尘暴中心距A市的距离最小,A市是否会受到影响,主要应比较AC与300km的大小,而AC可在Rt△ABC中由锐角三角函数求得.
【解】过点A作AC⊥BD于C,
在Rt△ABC中,∠ACB=90°,∠ABD=45°,AB=400km
∴AC=AB·sin∠ABC=AB·sin45°=400×=200(km)
∵200<300
∴A市会受到这次沙尘暴的影响.
【规律总结】近年来应用问题在中考中频繁出现,所以在平时学习中应培养将实际问题转化为数学问题的能力和意识.
2.今后的中考试题将更加侧重于考查运用垂径定理及其逆定理解决实际问题的能力.
【例2】如图所示,AB是⊙O的弦(非直径),C,D是AB上两点,并且AC=BD,求证OC=OD.
( http: / / )
【分析】过O作弦AB的弦心距OM是常见的辅助线.由垂径定理可知AM=BM,又由于AC=BD,则可知CM=DM,由线段的垂直平分线上的点到线段两个端点的距离相等可知OC=OD.
证明:过点O作OM⊥AB,垂足为M,由垂径定理得AM=BM,又∵AC=BD,∴CM=DM,
又∵OM⊥CD,∴OC=OD.
【规律总结】(1)解有关弦的问题,常常过圆心作弦的垂线段,利用垂径定理构造由半径、半弦、弦心距组成的直角三角形来解决.
(2)本题是利用垂径定理构造线段CD的垂直平分线来解决,其实本题也可以连结OA、OB,构造两三角形全等来解决.
3.圆周角定理及其推论建立了同弧所对的圆周角与圆心角之间的关系,从而与弧、弦、弦心距等建立了联系,因此在中考命题中圆周角定理及其推论常与其他知识点综合起来考查,在今后的中考中应关注创新类试题的出现.
【例3】已知:如图1,AB是⊙O的一条弦,点C为的中点,CD是⊙O的直径,过C点的直线L交AB所在直线于点E,交⊙O于点F.
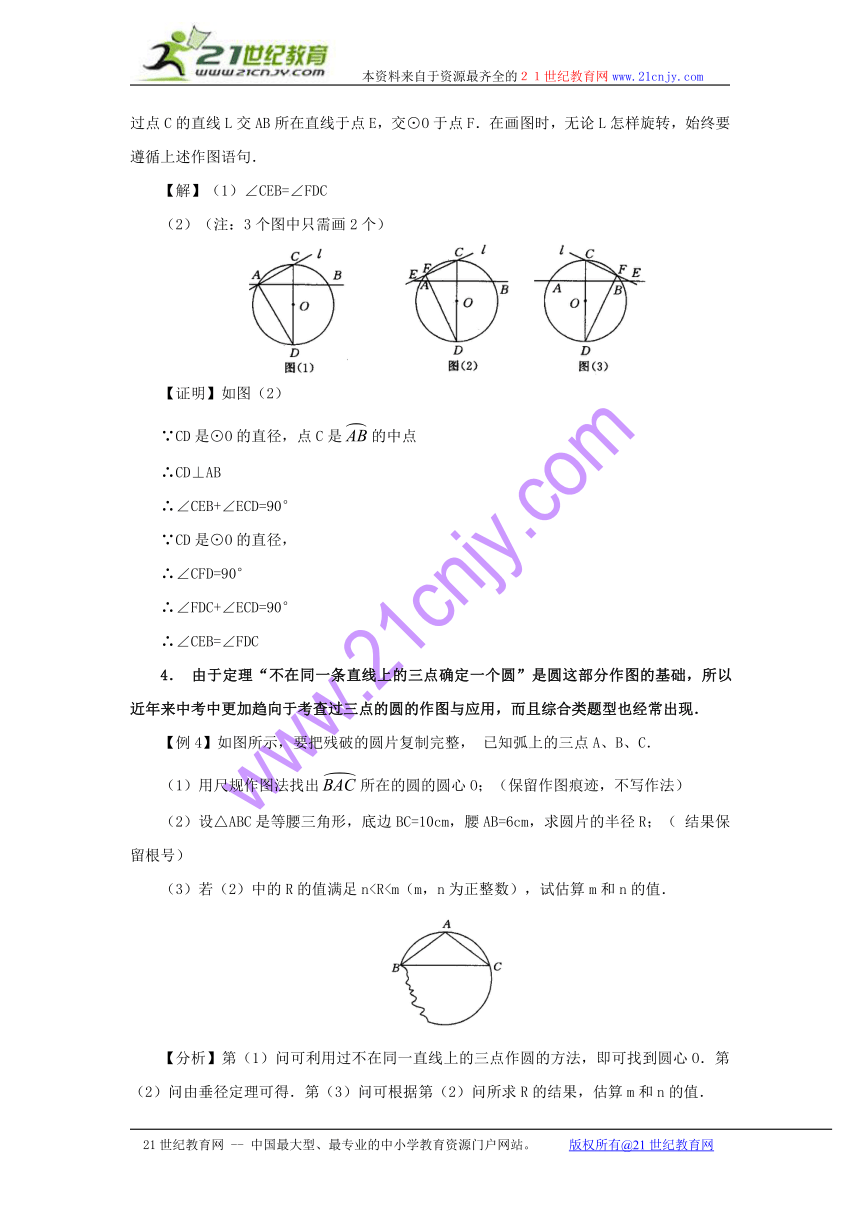
(1)判定图中∠CEB与∠FDC的数量关系,并写出结论:E点、F点的位置也随之变化,请你在图2的两个备用图中分别画出L在不同位置时,使(1)的结论仍然成立的图形,标上相应字母,选其中一个图形给予证明.
【分析】本题创新之处在于图(2)的两个备用图中要求学生自己画图,要注意题干中过点C的直线L交AB所在直线于点E,交⊙O于点F.在画图时,无论L怎样旋转,始终要遵循上述作图语句.
【解】(1)∠CEB=∠FDC
(2)(注:3个图中只需画2个)
( http: / / )
【证明】如图(2)
∵CD是⊙O的直径,点C是的中点
∴CD⊥AB
∴∠CEB+∠ECD=90°
∵CD是⊙O的直径,
∴∠CFD=90°
∴∠FDC+∠ECD=90°
∴∠CEB=∠FDC
4.由于定理“不在同一条直线上的三点确定一个圆”是圆这部分作图的基础,所以近年来中考中更加趋向于考查过三点的圆的作图与应用,而且综合类题型也经常出现.
【例4】如图所示,要把残破的圆片复制完整,已知弧上的三点A、B、C.
(1)用尺规作图法找出所在的圆的圆心O;(保留作图痕迹,不写作法)
(2)设△ABC是等腰三角形,底边BC=10cm,腰AB=6cm,求圆片的半径R;(结果保留根号)
(3)若(2)中的R的值满足n【分析】第(1)问可利用过不在同一直线上的三点作圆的方法,即可找到圆心O.第(2)问由垂径定理可得.第(3)问可根据第(2)问所求R的结果,估算m和n的值.
【解】(1)作AB、AC的垂直平分线,其交点即为圆心O,如图所示.
( http: / / )
(2)连结AO、BO,AO交BC于点M,
∵AB=AC
∴
∴OA⊥BC,且BM=CM=5cm
在Rt△AMB中,AM=cm
在Rt△BMO中,BO2-MO2=BM2
∴R2-(R-)2=52
解得R=
(3)∵=6
=5
∴5< <6
m=5,n=6
【规律总结】1.在解决有关半径或弦的计算问题时,常通过垂径定理,构造有半径、半弦、弦心距为边长的直角三角形.2.课标要求学生能够用有理数估计一个无理数的大致范围.本题第(3)问体现了这一精神.
5.圆的切线是一种基本的几何图形,它沟通了几何图形中角的数量关系.线的位置关系和线段间的数量关系,是中考必考的知识点,近几年的中考中有关切线的性质和判定和考查常结合圆的其他部分内容出题,题型多以综合题为主,要注意各知识点间的相互联系.
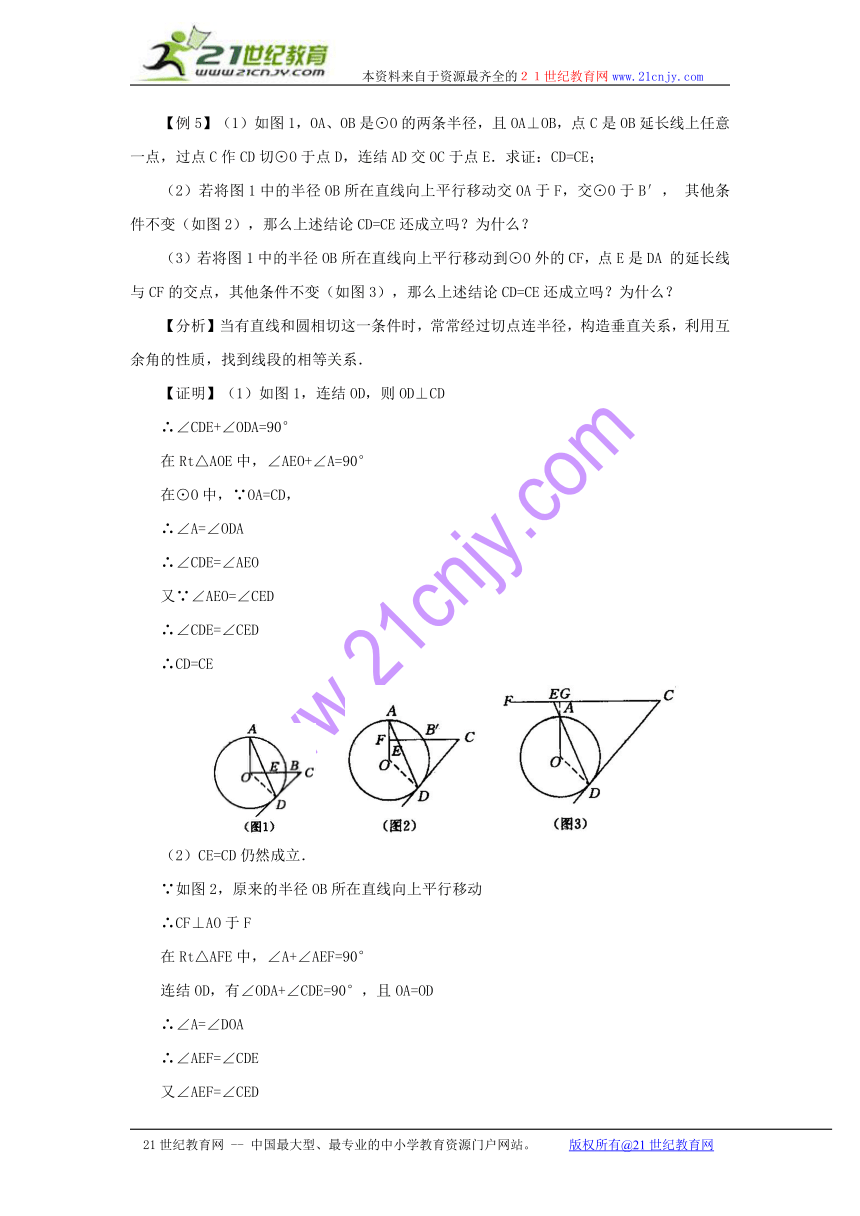
【例5】(1)如图1,OA、OB是⊙O的两条半径,且OA⊥OB,点C是OB延长线上任意一点,过点C作CD切⊙O于点D,连结AD交OC于点E.求证:CD=CE;
(2)若将图1中的半径OB所在直线向上平行移动交OA于F,交⊙O于B′,其他条件不变(如图2),那么上述结论CD=CE还成立吗?为什么?
(3)若将图1中的半径OB所在直线向上平行移动到⊙O外的CF,点E是DA的延长线与CF的交点,其他条件不变(如图3),那么上述结论CD=CE还成立吗?为什么?
【分析】当有直线和圆相切这一条件时,常常经过切点连半径,构造垂直关系,利用互余角的性质,找到线段的相等关系.
【证明】(1)如图1,连结OD,则OD⊥CD
∴∠CDE+∠ODA=90°
在Rt△AOE中,∠AEO+∠A=90°
在⊙O中,∵OA=CD,
∴∠A=∠ODA
∴∠CDE=∠AEO
又∵∠AEO=∠CED
∴∠CDE=∠CED
∴CD=CE
(2)CE=CD仍然成立.
∵如图2,原来的半径OB所在直线向上平行移动
∴CF⊥AO于F
在Rt△AFE中,∠A+∠AEF=90°
连结OD,有∠ODA+∠CDE=90°,且OA=OD
∴∠A=∠DOA
∴∠AEF=∠CDE
又∠AEF=∠CED
∴∠CED=∠CDE
∴CD=CE
(3)CE=CD仍然成立
∵如图3,原来的半径OB所在直线向上平行移动,
∴AO⊥CF
延长OA交CF于G,在Rt△AEG中,∠AEG+∠GAE=90°
连结OD,有∠CDA+∠ODA=90°,且OA=OD
∴∠ADO=∠OAD=∠GAE
∴∠CDE=∠CED
∴CD=CE
【规律总结】在某些图形变化过程中,某些几何关系保持不变.
【例6】
如图1,已知AB是⊙O的直径,AB垂直于弦CD,垂足为M,弦AE交CD于F,则有结论AD2=AE·AF成立(不要求证明).
(1)若将弦CD向下平移至与⊙O相切于B点时,如图2,则AE.AF是否等于AG?如果不相等,请探求AE.AF等于哪两条线段的积?并给出证明.
(2)当CD继续向下平移至与⊙O相离时,如图3,在(1)中探求的结论是否还成立,并说明理由.
( http: / / )
【分析】在图2,图3中分别连结BG,EG,证△AEG∽△AHF可得结论AE·AF=AG·AH.
【解】(1)AE·AF不等于AG,应该有结论AE·AF=AG·AH.
【证明】如图1,连结BG,EG.
∵AB是⊙O的直径,CD是⊙O的切线,
∴∠ABF=∠AGB=90°
∴∠BAF+∠BFA=90°
∴∠AGE+∠BGE=90°
∴∠BAF+∠BFA=∠AGE+∠BGE
而∠BAF=∠BGE,
∴∠BFA=∠AGE
又∵∠FAH=∠GAE
∴△AEG∽△AHF
∴
即AE·AF=AG·AH
(2)(1)探求的结论还成立
证明:连结BG,EG.
∵AB是⊙O的直径
AM⊥CD
∴∠AMF=∠AGB=90°
∴∠AFM+∠FAM=∠AGE+∠BGE=90°
而∵∠FAM=∠BGE
∴∠AFM=∠AGE
又∵∠FAH=∠GAE
∴△AEG∽△AHF
∴
∴AE·AF=AG·AH
【规律总结】在某些图形变化过程中,所连辅助线,所用解题方法基本不变.
6.涉及两圆的位置关系及两圆相切的性质的计算与证明是中考必考的知识点,其中有关两圆的位置关系的分类讨论题、两圆相切的性质的探索题以及与函数有关的综合题是近几年中考的新题型.
【例7】已知:如图,⊙A与⊙B外切于点C,DE是两圆的一条外公切线,切点分别为D、E.
(1)判断△DCE的形状并证明.
(2)过点C作CO⊥DE,垂足为O,以直线DE为x轴,直线OC为y轴建立直角坐标系,且OE=2,OD=8,求经过D、C、E三点的抛物线的函数解析式,并求出抛物线的顶点坐标;
(3)这条抛物线的顶点是否在连心线AB上?如果在,请你证明;如果不在,说明理由.
( http: / / )
【分析】(1)、(2)问易求,第(3)问应求出A、B两点坐标,为此首先应求出两圆半径.在两圆相切的有关问题中,遇计算问题,一般利用两圆的连心线,连结经过切点的半径,过小圆圆心作大圆半径的垂线,通过所构成的直角三角形解决问题.
【解】(1)△DCE是直角三角形.
过C点作⊙A和⊙B的内公切线交DE于F,则FC=FD,FC=FE,
∴FC是△CDE的中线,且FC=DE
∴△DCE是直角三角形,∠DCE=90°
(2)在Rt△DCE中,CO⊥DE于O点,△DOC∽△COE
∴OC2=OD·OE=16,OC=4,C点坐标(0,4).
设经过D、C、E三点的抛物线的解析式为y=ax2+bx+c或者y=a(x-x1)(x-x2),把D(-8,0),E(2,0),C(0,4)代入解析式,解得:
y=-x2-x+4
∴顶点坐标是(-3,)
(3)答:抛物线的顶点,在连心线AB上,证明如下:
如图15-5,连结AD、BE,过B点作BG⊥AD于G,
设⊙A半径为R,⊙B半径为r
∴AD∥CO∥BE
∴AC:CB=DO:OE=4:1
在Rt△AGB中,AB2=AG2+BG2,
∴r=,r=10
∴A点坐标(-8,10),B点坐标(2,)
设直线AB的解析式为y=kx+b(k≠0),解得y=-x+4,
把抛物线顶点坐标(-3,)代入直线的解析式,左边=右边=,
∴抛物线y=-x2-+4的顶点P(-3,)在连心线AB上.
7.扇形和弓形的面积是中考的重点考查内容,近几年来对不规则几何图形面积的计算在各省、市中考题中频繁出现,成为中考的一个热点,该类型题主要考查对图形面积的转化和割补能力.还应关注一些实际问题的解决,以培养学生运用所学知识解决实际问题的能力.
【例8】当汽车在雨天行驶时,为了看清楚道路,司机要启动前方挡风玻璃上的雨刷器.如图15-6是某汽车的一个雨刷器的示意图,雨刷器杆AB与雨刷CD在B处固定连结(不能转动),当杆AB绕A点转动90°时,雨刷CD扫过的面积是多少呢?小明仔细观察了雨刷器的转动情况,量得CD=80cm,∠DBA=20°,端点C、D与A的距离分别是115cm、35cm.他经过认真思考只选用了其中的部分数据就求得了结果,你知道小明是怎样计算的吗?也请你算一算雨刷CD扫过的面积为______cm2(取3.14).
【分析】求雨刷CD扫过的面积,首先应关注CD到C′D′的运动过程,弄清所求面积包括哪些部分,然后用割补法,把这部分面积变成以AC为半径、圆心角为90°的扇形面积与以AD为半径,圆心角为90°的扇形面积的差.
【解】所求面积为(115+35)(115-35)=150×20=9420
故应填9420
【例9】如图所示.梯形ABCD中,AD∥BC,∠D=90°,以AB为直径的⊙O切CD于E,交BC于F,若AB=4cm,AD=1cm,则图中阴影部分的面积为______cm2.(不用近似值)
【分析】连结AF.可证四边形AFCD为矩形,FC=AD=1cm,OE=AB=2cm,OE⊥CD.
M为AF与OE的交点
∴ME=FC=1cm,OM=OE-ME=1cm
由OM∥BC,OA=OB,OM=OE-ME=1cm
可知M为AF中点,
∴BF=2OM=2cm
在Rt△ABF中,BF=AB
∴∠BAF=30°
∴∠BOF=60°
由OB=OF
∴∠B=60°
∴∠AOE=∠B=60°
∴∠EOF=60°
∴阴影部分面积等于Rt△ECF的面积(△BOF与△FOE为全等的等边三角形)
在△EFC中,∠C=90°,∠EFC=180°-2×60°=60°
∴∠FEC=30°
∴EC=FC=cm2
∴S阴影部分=S△EFC=EC·FC=××1=cm2
【解】应填
8.近年中考中以圆锥侧面展开图的面积计算为主的题型频繁出现,解此类题的关键是区分平面图形中各元素和立体图形中各元素的对应关系.
【例10】如图所示,点B在圆锥母线VA上,且VA=VA,过点B作平行于底面的平面截得一个小圆锥,若小圆锥的侧面积为S,原圆锥的侧面积为S,则下列判断中正确的是( )
A.S1=S B.S1=S C.S1=S D.S1=S
【分析】如图是圆锥的侧面展开图.
S1=
∵VB=VA
∴S1=S
【解】选D
【规律总结】圆锥侧面展开图的计算关键是区分平面图形中各元素和立体图形中各元素的对应关系.圆锥中的母线就是其侧面展开图中扇形的半径.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
二、考点与命题趋向分析
(一)能力
1.理解圆及其有关概念,了解弧、弦、圆心角的关系,探索并了解点与圆、直线与圆以及圆与圆的位置关系.
2.探索圆的性质,了解圆周角与圆心角的关系、直径所对圆周角的特征.
3.了解三角形的内心和外心.
4.了解切线的概念,探索切线与过切点的半径之间的关系;能判定一条直线是否为圆的切线,会过圆上一点画圆的切线.
5.会计算弧长及扇形的面积,会计算圆锥的侧面积和全面积.
(二)命题趋向分析
1.今后的中考试题将更侧重在于具体问题中考查圆的定义及点与圆的位置关系,应在学习中侧重于如何运用如何解决实际问题.
【例1】由于过渡采伐森林和破坏植被,使我国某些地区多次受到沙尘暴的侵袭.近日A市气象局测得沙尘暴中心在A市正东方向400km的B处,正在向西北方向转移(如图所示),距沙尘暴中心300km的范围内将受其影响,问A市是否会受到这次沙尘暴的影响?
【分析】过点A作AC⊥BD交BD于点C,由题意可知沙尘暴中心正沿BD方向移动,当它移动到点C时,沙尘暴中心距A市的距离最小,A市是否会受到影响,主要应比较AC与300km的大小,而AC可在Rt△ABC中由锐角三角函数求得.
【解】过点A作AC⊥BD于C,
在Rt△ABC中,∠ACB=90°,∠ABD=45°,AB=400km
∴AC=AB·sin∠ABC=AB·sin45°=400×=200(km)
∵200<300
∴A市会受到这次沙尘暴的影响.
【规律总结】近年来应用问题在中考中频繁出现,所以在平时学习中应培养将实际问题转化为数学问题的能力和意识.
2.今后的中考试题将更加侧重于考查运用垂径定理及其逆定理解决实际问题的能力.
【例2】如图所示,AB是⊙O的弦(非直径),C,D是AB上两点,并且AC=BD,求证OC=OD.
( http: / / )
【分析】过O作弦AB的弦心距OM是常见的辅助线.由垂径定理可知AM=BM,又由于AC=BD,则可知CM=DM,由线段的垂直平分线上的点到线段两个端点的距离相等可知OC=OD.
证明:过点O作OM⊥AB,垂足为M,由垂径定理得AM=BM,又∵AC=BD,∴CM=DM,
又∵OM⊥CD,∴OC=OD.
【规律总结】(1)解有关弦的问题,常常过圆心作弦的垂线段,利用垂径定理构造由半径、半弦、弦心距组成的直角三角形来解决.
(2)本题是利用垂径定理构造线段CD的垂直平分线来解决,其实本题也可以连结OA、OB,构造两三角形全等来解决.
3.圆周角定理及其推论建立了同弧所对的圆周角与圆心角之间的关系,从而与弧、弦、弦心距等建立了联系,因此在中考命题中圆周角定理及其推论常与其他知识点综合起来考查,在今后的中考中应关注创新类试题的出现.
【例3】已知:如图1,AB是⊙O的一条弦,点C为的中点,CD是⊙O的直径,过C点的直线L交AB所在直线于点E,交⊙O于点F.
(1)判定图中∠CEB与∠FDC的数量关系,并写出结论:E点、F点的位置也随之变化,请你在图2的两个备用图中分别画出L在不同位置时,使(1)的结论仍然成立的图形,标上相应字母,选其中一个图形给予证明.
【分析】本题创新之处在于图(2)的两个备用图中要求学生自己画图,要注意题干中过点C的直线L交AB所在直线于点E,交⊙O于点F.在画图时,无论L怎样旋转,始终要遵循上述作图语句.
【解】(1)∠CEB=∠FDC
(2)(注:3个图中只需画2个)
( http: / / )
【证明】如图(2)
∵CD是⊙O的直径,点C是的中点
∴CD⊥AB
∴∠CEB+∠ECD=90°
∵CD是⊙O的直径,
∴∠CFD=90°
∴∠FDC+∠ECD=90°
∴∠CEB=∠FDC
4.由于定理“不在同一条直线上的三点确定一个圆”是圆这部分作图的基础,所以近年来中考中更加趋向于考查过三点的圆的作图与应用,而且综合类题型也经常出现.
【例4】如图所示,要把残破的圆片复制完整,已知弧上的三点A、B、C.
(1)用尺规作图法找出所在的圆的圆心O;(保留作图痕迹,不写作法)
(2)设△ABC是等腰三角形,底边BC=10cm,腰AB=6cm,求圆片的半径R;(结果保留根号)
(3)若(2)中的R的值满足n
【解】(1)作AB、AC的垂直平分线,其交点即为圆心O,如图所示.
( http: / / )
(2)连结AO、BO,AO交BC于点M,
∵AB=AC
∴
∴OA⊥BC,且BM=CM=5cm
在Rt△AMB中,AM=cm
在Rt△BMO中,BO2-MO2=BM2
∴R2-(R-)2=52
解得R=
(3)∵=6
=5
∴5< <6
m=5,n=6
【规律总结】1.在解决有关半径或弦的计算问题时,常通过垂径定理,构造有半径、半弦、弦心距为边长的直角三角形.2.课标要求学生能够用有理数估计一个无理数的大致范围.本题第(3)问体现了这一精神.
5.圆的切线是一种基本的几何图形,它沟通了几何图形中角的数量关系.线的位置关系和线段间的数量关系,是中考必考的知识点,近几年的中考中有关切线的性质和判定和考查常结合圆的其他部分内容出题,题型多以综合题为主,要注意各知识点间的相互联系.
【例5】(1)如图1,OA、OB是⊙O的两条半径,且OA⊥OB,点C是OB延长线上任意一点,过点C作CD切⊙O于点D,连结AD交OC于点E.求证:CD=CE;
(2)若将图1中的半径OB所在直线向上平行移动交OA于F,交⊙O于B′,其他条件不变(如图2),那么上述结论CD=CE还成立吗?为什么?
(3)若将图1中的半径OB所在直线向上平行移动到⊙O外的CF,点E是DA的延长线与CF的交点,其他条件不变(如图3),那么上述结论CD=CE还成立吗?为什么?
【分析】当有直线和圆相切这一条件时,常常经过切点连半径,构造垂直关系,利用互余角的性质,找到线段的相等关系.
【证明】(1)如图1,连结OD,则OD⊥CD
∴∠CDE+∠ODA=90°
在Rt△AOE中,∠AEO+∠A=90°
在⊙O中,∵OA=CD,
∴∠A=∠ODA
∴∠CDE=∠AEO
又∵∠AEO=∠CED
∴∠CDE=∠CED
∴CD=CE
(2)CE=CD仍然成立.
∵如图2,原来的半径OB所在直线向上平行移动
∴CF⊥AO于F
在Rt△AFE中,∠A+∠AEF=90°
连结OD,有∠ODA+∠CDE=90°,且OA=OD
∴∠A=∠DOA
∴∠AEF=∠CDE
又∠AEF=∠CED
∴∠CED=∠CDE
∴CD=CE
(3)CE=CD仍然成立
∵如图3,原来的半径OB所在直线向上平行移动,
∴AO⊥CF
延长OA交CF于G,在Rt△AEG中,∠AEG+∠GAE=90°
连结OD,有∠CDA+∠ODA=90°,且OA=OD
∴∠ADO=∠OAD=∠GAE
∴∠CDE=∠CED
∴CD=CE
【规律总结】在某些图形变化过程中,某些几何关系保持不变.
【例6】
如图1,已知AB是⊙O的直径,AB垂直于弦CD,垂足为M,弦AE交CD于F,则有结论AD2=AE·AF成立(不要求证明).
(1)若将弦CD向下平移至与⊙O相切于B点时,如图2,则AE.AF是否等于AG?如果不相等,请探求AE.AF等于哪两条线段的积?并给出证明.
(2)当CD继续向下平移至与⊙O相离时,如图3,在(1)中探求的结论是否还成立,并说明理由.
( http: / / )
【分析】在图2,图3中分别连结BG,EG,证△AEG∽△AHF可得结论AE·AF=AG·AH.
【解】(1)AE·AF不等于AG,应该有结论AE·AF=AG·AH.
【证明】如图1,连结BG,EG.
∵AB是⊙O的直径,CD是⊙O的切线,
∴∠ABF=∠AGB=90°
∴∠BAF+∠BFA=90°
∴∠AGE+∠BGE=90°
∴∠BAF+∠BFA=∠AGE+∠BGE
而∠BAF=∠BGE,
∴∠BFA=∠AGE
又∵∠FAH=∠GAE
∴△AEG∽△AHF
∴
即AE·AF=AG·AH
(2)(1)探求的结论还成立
证明:连结BG,EG.
∵AB是⊙O的直径
AM⊥CD
∴∠AMF=∠AGB=90°
∴∠AFM+∠FAM=∠AGE+∠BGE=90°
而∵∠FAM=∠BGE
∴∠AFM=∠AGE
又∵∠FAH=∠GAE
∴△AEG∽△AHF
∴
∴AE·AF=AG·AH
【规律总结】在某些图形变化过程中,所连辅助线,所用解题方法基本不变.
6.涉及两圆的位置关系及两圆相切的性质的计算与证明是中考必考的知识点,其中有关两圆的位置关系的分类讨论题、两圆相切的性质的探索题以及与函数有关的综合题是近几年中考的新题型.
【例7】已知:如图,⊙A与⊙B外切于点C,DE是两圆的一条外公切线,切点分别为D、E.
(1)判断△DCE的形状并证明.
(2)过点C作CO⊥DE,垂足为O,以直线DE为x轴,直线OC为y轴建立直角坐标系,且OE=2,OD=8,求经过D、C、E三点的抛物线的函数解析式,并求出抛物线的顶点坐标;
(3)这条抛物线的顶点是否在连心线AB上?如果在,请你证明;如果不在,说明理由.
( http: / / )
【分析】(1)、(2)问易求,第(3)问应求出A、B两点坐标,为此首先应求出两圆半径.在两圆相切的有关问题中,遇计算问题,一般利用两圆的连心线,连结经过切点的半径,过小圆圆心作大圆半径的垂线,通过所构成的直角三角形解决问题.
【解】(1)△DCE是直角三角形.
过C点作⊙A和⊙B的内公切线交DE于F,则FC=FD,FC=FE,
∴FC是△CDE的中线,且FC=DE
∴△DCE是直角三角形,∠DCE=90°
(2)在Rt△DCE中,CO⊥DE于O点,△DOC∽△COE
∴OC2=OD·OE=16,OC=4,C点坐标(0,4).
设经过D、C、E三点的抛物线的解析式为y=ax2+bx+c或者y=a(x-x1)(x-x2),把D(-8,0),E(2,0),C(0,4)代入解析式,解得:
y=-x2-x+4
∴顶点坐标是(-3,)
(3)答:抛物线的顶点,在连心线AB上,证明如下:
如图15-5,连结AD、BE,过B点作BG⊥AD于G,
设⊙A半径为R,⊙B半径为r
∴AD∥CO∥BE
∴AC:CB=DO:OE=4:1
在Rt△AGB中,AB2=AG2+BG2,
∴r=,r=10
∴A点坐标(-8,10),B点坐标(2,)
设直线AB的解析式为y=kx+b(k≠0),解得y=-x+4,
把抛物线顶点坐标(-3,)代入直线的解析式,左边=右边=,
∴抛物线y=-x2-+4的顶点P(-3,)在连心线AB上.
7.扇形和弓形的面积是中考的重点考查内容,近几年来对不规则几何图形面积的计算在各省、市中考题中频繁出现,成为中考的一个热点,该类型题主要考查对图形面积的转化和割补能力.还应关注一些实际问题的解决,以培养学生运用所学知识解决实际问题的能力.
【例8】当汽车在雨天行驶时,为了看清楚道路,司机要启动前方挡风玻璃上的雨刷器.如图15-6是某汽车的一个雨刷器的示意图,雨刷器杆AB与雨刷CD在B处固定连结(不能转动),当杆AB绕A点转动90°时,雨刷CD扫过的面积是多少呢?小明仔细观察了雨刷器的转动情况,量得CD=80cm,∠DBA=20°,端点C、D与A的距离分别是115cm、35cm.他经过认真思考只选用了其中的部分数据就求得了结果,你知道小明是怎样计算的吗?也请你算一算雨刷CD扫过的面积为______cm2(取3.14).
【分析】求雨刷CD扫过的面积,首先应关注CD到C′D′的运动过程,弄清所求面积包括哪些部分,然后用割补法,把这部分面积变成以AC为半径、圆心角为90°的扇形面积与以AD为半径,圆心角为90°的扇形面积的差.
【解】所求面积为(115+35)(115-35)=150×20=9420
故应填9420
【例9】如图所示.梯形ABCD中,AD∥BC,∠D=90°,以AB为直径的⊙O切CD于E,交BC于F,若AB=4cm,AD=1cm,则图中阴影部分的面积为______cm2.(不用近似值)
【分析】连结AF.可证四边形AFCD为矩形,FC=AD=1cm,OE=AB=2cm,OE⊥CD.
M为AF与OE的交点
∴ME=FC=1cm,OM=OE-ME=1cm
由OM∥BC,OA=OB,OM=OE-ME=1cm
可知M为AF中点,
∴BF=2OM=2cm
在Rt△ABF中,BF=AB
∴∠BAF=30°
∴∠BOF=60°
由OB=OF
∴∠B=60°
∴∠AOE=∠B=60°
∴∠EOF=60°
∴阴影部分面积等于Rt△ECF的面积(△BOF与△FOE为全等的等边三角形)
在△EFC中,∠C=90°,∠EFC=180°-2×60°=60°
∴∠FEC=30°
∴EC=FC=cm2
∴S阴影部分=S△EFC=EC·FC=××1=cm2
【解】应填
8.近年中考中以圆锥侧面展开图的面积计算为主的题型频繁出现,解此类题的关键是区分平面图形中各元素和立体图形中各元素的对应关系.
【例10】如图所示,点B在圆锥母线VA上,且VA=VA,过点B作平行于底面的平面截得一个小圆锥,若小圆锥的侧面积为S,原圆锥的侧面积为S,则下列判断中正确的是( )
A.S1=S B.S1=S C.S1=S D.S1=S
【分析】如图是圆锥的侧面展开图.
S1=
∵VB=VA
∴S1=S
【解】选D
【规律总结】圆锥侧面展开图的计算关键是区分平面图形中各元素和立体图形中各元素的对应关系.圆锥中的母线就是其侧面展开图中扇形的半径.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
