5.2不等式的基本性质

课件26张PPT。5.2 不等式的基本性质2010.9.15 1、如果a = b,b = c,那么a = c （ ）依据：
热身运动等式的传递性下列说法是否正确，并说明理由 等式的基本性质1
2、如果a = b,那么a+3 = b+3（ ）依据： 3、如果a = b，那么3a = 3b 或 （ ）

依据：
等式的基本性质2




猜想：不等式是否也具有传递性？？如果a =b，b = c, 那么a = c如果a b，b c, 那么a c＜===＜＜一、探索猜想
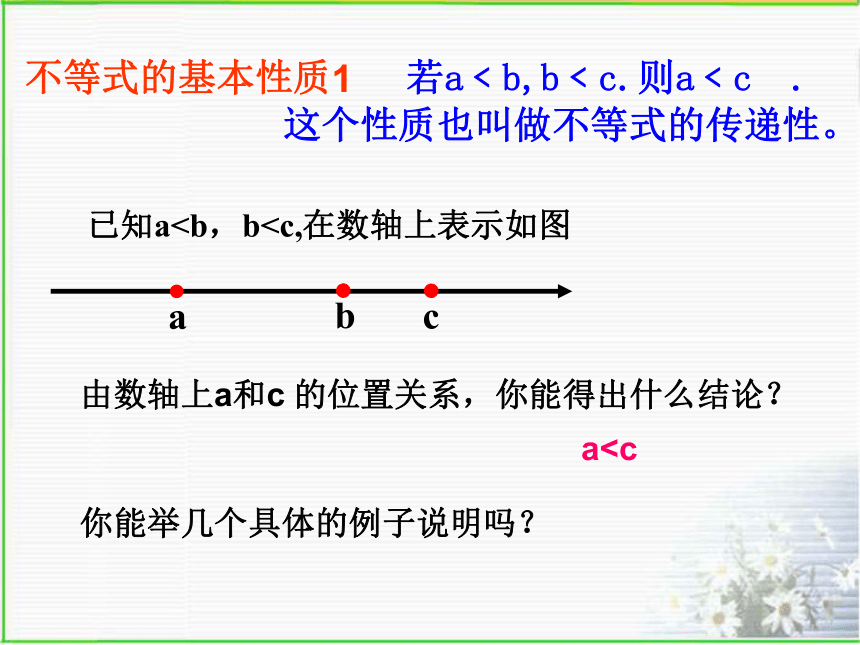
1、等式具有传递性：不等式的基本性质1 若a﹤b,b﹤c.则a﹤c .
这个性质也叫做不等式的传递性。由数轴上a和c 的位置关系，你能得出什么结论？a你能举几个具体的例子说明吗？猜想：不等式是否也具有类似的性质？如果a = b，那么a +c= b+ c，a –c= b- c
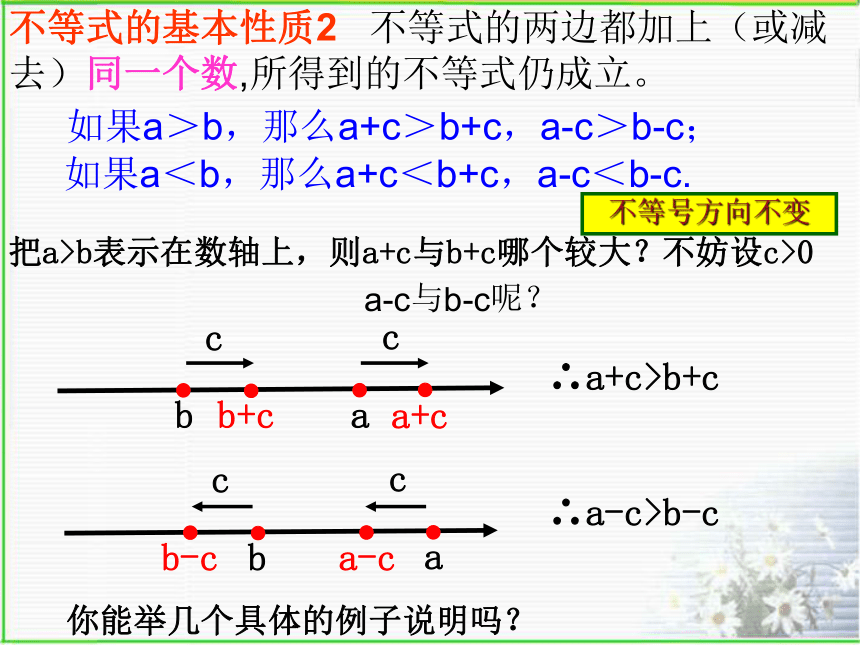
2.等式的基本性质1:等式的两边都加上（或减去）同一个数 ，等式仍然成立。如果a＞b，那么a +c＞b+ c，a –c ＞b- c？cccc把a>b表示在数轴上，则a+c与b+c哪个较大？

不妨设c>0∴a+c>b+c∴a-c>b-c a-c与b-c呢？不等号方向不变 如果a＜b，那么a+c＜b+c，a-c＜b-c.如果a＞b，那么a+c＞b+c，a-c＞b-c；不等式的基本性质2 不等式的两边都加上（或减
去）同一个数,所得到的不等式仍成立。你能举几个具体的例子说明吗？2、选择适当的不等号填空，并说明理由.<≥≥做一做：1、（2010鄂州）根据下图所示，对a、b、c三种物体的质量判断正确的是（ ）
A、ac D、b探索猜想：猜想：不等式是否也具有类似的性质？？ 某同学在完成上题后，归纳认为：不等式的两边都乘以（或除以）同一个数，所得到的不等式仍成立。你认为对吗？为什么？想一想： 8＿＿12
8×4＿＿12×4
8÷2＿＿12÷2＜＜＜ 8＿＿12
8×(-4)＿＿12×(-4)
8÷(-2)＿＿12÷(-2)>>＜ 不等式的两边都乘 (或都除以)同一个正数，所得的不等式仍成立；
不等式的两边都乘（或都除以）同一个负数，必须把不等号的方向改变，所得的不等式成立.即:如果a＞b，且c＞0，那么ac＞bc， ＞ ；
如果a＞b，且c＜0，那么ac＜bc ， ＜ ；不等式的基本性质3二、探索发现等式的基本性质2 等式的两边都乘以（或除以）
同一个数（除数不能为零）, 等式仍成立。归纳：不等式的基本性质：性质3：不等式的两边都乘(或都除以)同一个正数,所得到的不等式仍成立；
不等式的两边都乘(或都除以)同一个负数,必须把不等号的方向改变,所得到的不等式成立.性质1：若a＜b，b＜c，则a＜c。性质2：不等式的两边都加上(或减去)同一个数,所得到的不等式仍成立.（不等号方向不变）（不等号方向不变）（不等号方向改变）（传递性）(1)若x+1>0，两边同加上-1，
得_________ (依据：_____________ )；
(2)若2x>-6，两边同除以2，
得_________ (依据：_____________ )；
(3)若 x≤ ，两边同乘 -3，
得 _________ (依据：________________). x>-1 不等式的基本性质2不等式的基本性质3x>-3 不等式的基本性质3练一练：填空： 选择适当的不等号,并说明理由
（1）已知a>b,则a+1 b+1 （ ）
（2）已知a≤b,则-3a -3bb（ ）
（3）已知a 2a-3 2b-3 （ ）
（4）已知-3a+2 -3b+2,
则-3a -3b（ ）
a b （ ）≤><<≤不等式基本性质2不等式基本性质3不等式基本性质2不等式基本性质2不等式基本性质3 ≥不等式基本性质3
≥试一试：　如图,在数轴上分别表示2a和a的点(a＜0).
2a位于a的左边，所以2a＜a.
解法二：（数形结合）例　已知a<0 ，试比较2a与a的大小.解法一：（不等式的基本性质3）∵2＞1，a＜0，
∴2a＜a.想一想：还有其他比较2a与a的大小的方法吗？三、挑战自我解法三：（利用不等式基本性质2）∵a＜0，
∴ a+a＜0+a，
即2a ＜a.例　已知a<0 ，试比较2a与a的大小.解法四: （差值法）∵2a－a=a ＜0，
∴2a＜a.商值法特殊值法思考：当a ＞ 0时a = 0时
判断正误，并说明理由

（1）由5 ﹥ 4，可得5a ﹥ 4a ( )
（2）已知a ﹥ b，可得ac2 ﹥ bc2 ( )
（2）已知ac2 ﹥ bc2 ，可得a ﹥ b ( )
××拓展提升? 四、探究活动
比较等式与不等式的基本性质.
例如：等式是否有与不等式的基本性 质1类似的传递性？
不等式是否有与等式的基本性质类似的移项法则？
你可以用列表的方式进行对比.（请与你的伙伴交流）
若a=b，b=c，则a=c。若a＜b，b＜c，则a＜c。如果a＞b,那么
a+c＞b+c，a-c＞b-c如果a=b，那么
a+c=b+c，a-c=b-c等式与不等式的基本性质的区别与联系通过这节课的学习活动你有哪些收获？1、不等式的基本性质：性质3：不等式的两边都乘(或都除以)同一个正数,所得到的不等式仍成立；
不等式的两边都乘(或都除以)同一个负数,必须把不等号的方向改变,所得到的不等式成立.性质1：若a＜b，b＜c，则a＜c。性质2：不等式的两边都加上(或减去)同一个数,所得到的不等式仍成立.（不等号方向不变）（不等号方向不变）（不等号方向改变）（传递性）小结: 2、学习了三种数学思想方法：类比思想、数形结合思想、分类讨论思想作业：
1、作业本二
2、课本p102页的作业题再 见　　我国于2001年12月11日正式加入世界贸易组织（WTO）。加入前，产品A的进口税超过产品B的进口税的1倍以上；加入后，这两种产品的进口税都下调了15%。你认为加入后产品A的进口税仍超过产品B的进口税的1倍以上吗？请说明理由。　 解：设加入前产品A、B的进口税分别为a美元、b美元。由题意,得,a>2b。加入后A、B两种产品的进口税分别为（1-15%）a元， （1-15%）b元，由不等式的基本性质3，
∵　1-15%＞0
∴（1-15%）a＞2 （1-15%）b
即表示产品A的进口税仍超过产品B的进口税的1倍以上。学以致用 老王和小李在同一家公司工作。老王每月的工资
原来比小张要高，但不到他的两倍。新年开始时，
公司给他们同时加薪10%，问加薪后老王的工资
仍比小张的工资高，但低于两倍吗？请说明理由。
如果是每个月各加薪200元呢？思考有理数a.b.c在数轴上的对应点如图所示 用“﹤”或“﹥”填空

①a+b_____a+c

②ab_____ac

③ac_____bc﹤﹤﹤挑战自我：