1.1认识三角形（二）

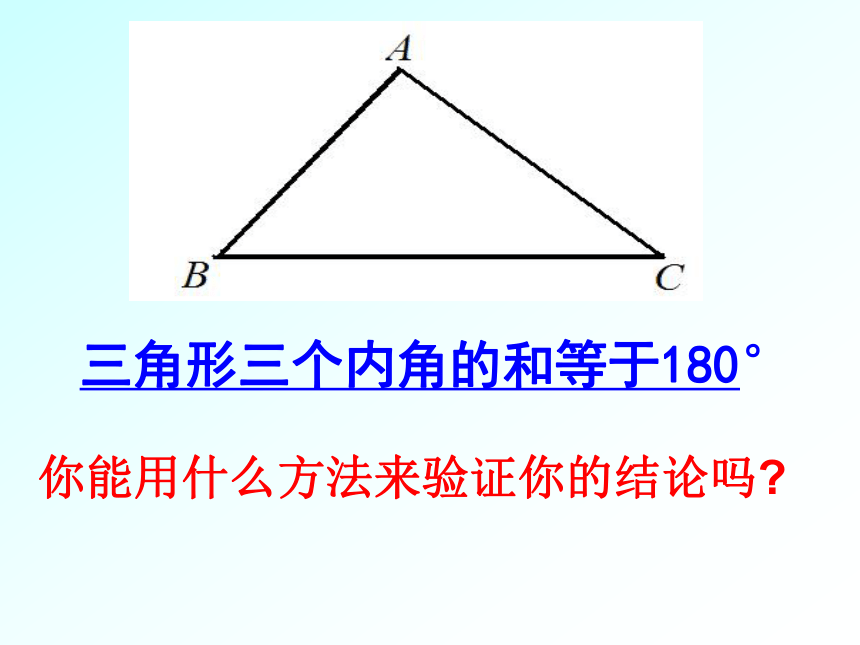
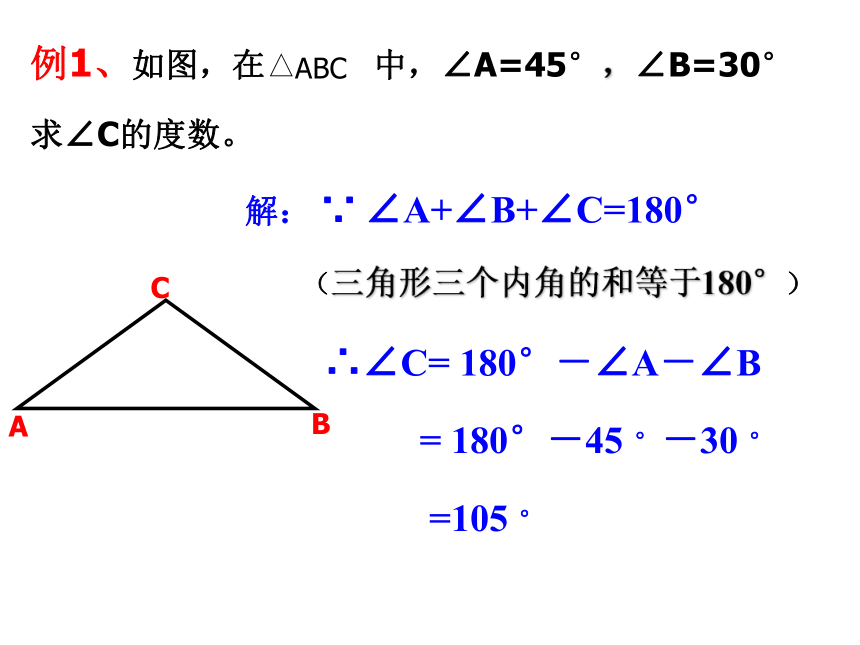
课件23张PPT。 由不在同一直线上的三条线段，首尾顺次相接所组成的图形叫做三角形.1.怎样的图形叫做三角形2.三角形有哪两个性质 三角形任何两边的和大于第三边,三角形任何两边的差小于第三边.复习回顾应用性质:判断三条线段能否构成一个三角形.性质应用1、下列各组数不可能是一个三角形的边长的是（ ）C情境两位同学分别画了一个三角形，甲说他所画的三角形的三个内角为30o、80o、100o；乙说他所画的三角形的三个内角为40o、60o、80o。你能判断他们谁说的是真的吗？为什么？三角形三个内角的和等于180°三角形的内角和定理：真真假假：你能用什么方法来验证你的结论吗?三角形三个内角的和等于180°CAB解： ∵ ∠A+∠B+∠C=180°（三角形三个内角的和等于180°）∴∠C= 180°－∠A－∠B
= 180°－45 °－30 °
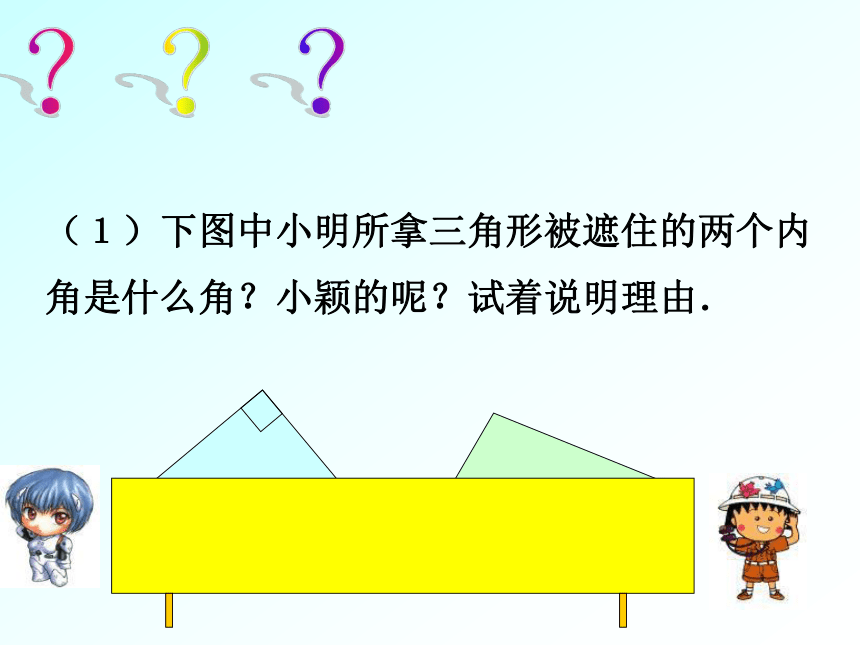
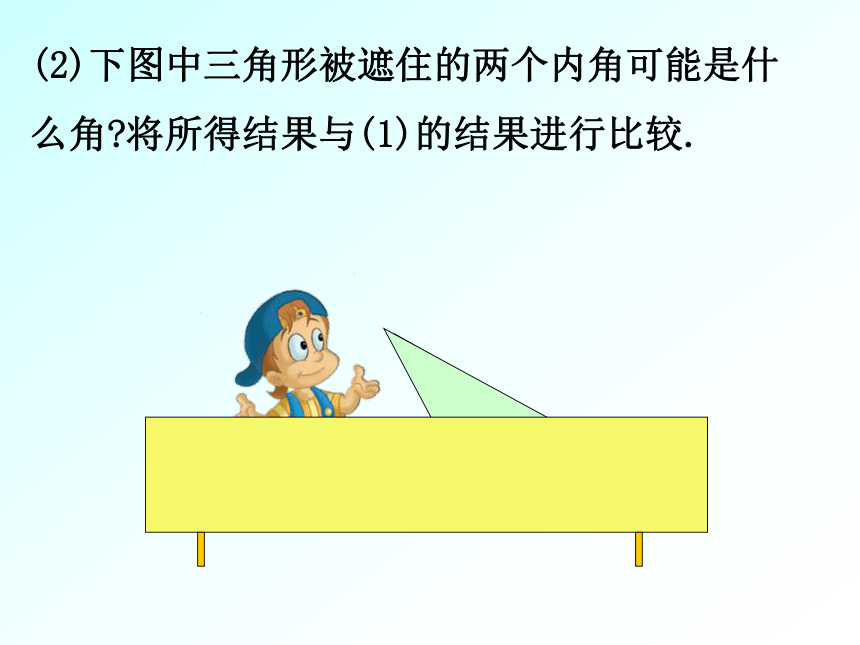
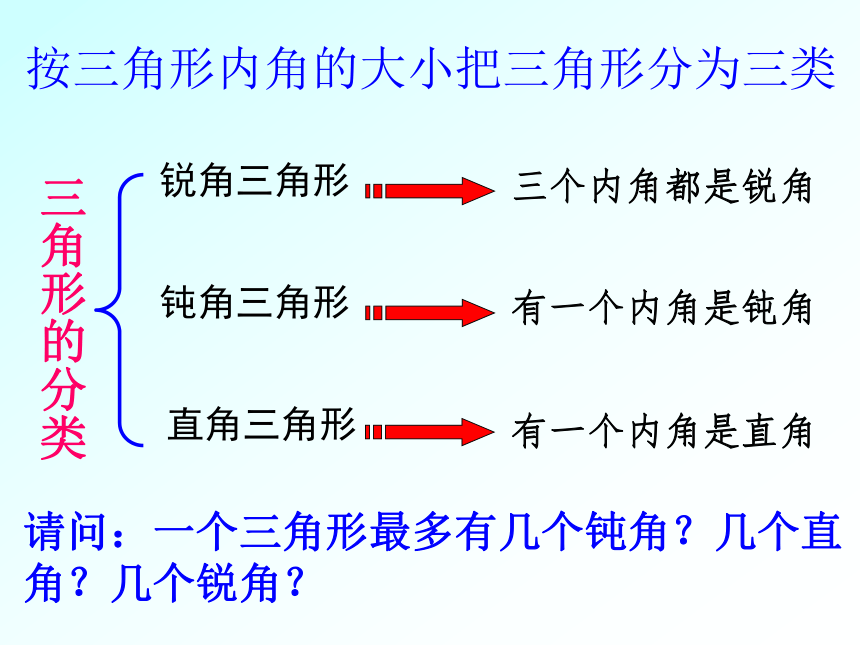
=105 ° （１）下图中小明所拿三角形被遮住的两个内角是什么角？小颖的呢？试着说明理由．？？？(2)下图中三角形被遮住的两个内角可能是什么角?将所得结果与(1)的结果进行比较.按三角形内角的大小把三角形分为三类锐角三角形三个内角都是锐角钝角三角形有一个内角是钝角直角三角形有一个内角是直角请问：一个三角形最多有几个钝角？几个直角？几个锐角？1、判断正误：
①三角形内角中至少有两个锐角 ( )
②三角形内角中至少有一个钝角 ( )
②三角形内角中最多有一个直角 ( )
②三角形内角中必有一个角大于60° ( )
对错对对DBAC　　让我们再来认识一下与三角形的内角相关的另外一种角：三角形的外角 ．　　由三角形一条边的延长线和另一条相邻边组成的角叫做该三角形的外角。思考:一个三角形有多少个外角?（2）∠2既是______的内角，
又是______的外角2、如图：∠1△BCD△ADC（1）△BCD的外角是_____1、如图，∠1、∠2、∠3
是不是△ABC的外角？辨一辨：DBAC不相邻内角1234 ．∠3+∠4=180°观 察 ： 外角与不相邻内角有什么关系？(1) ∠4=∠1+∠2，∠4﹥∠1 ， ∠4﹥∠2。 数学说理:∵∠3+∠4=180°∴ ∠4=∠1+∠2 。 ∠1+∠2+∠3=180°DBAC不相邻内角1234 ．探索，猜想：观 察 ：DBAC不相邻内角1234 ． 1、三角形的一个外角等于和它不相邻的两个内角的和。 2、三角形的一个外角大于任何一个和它不相邻的内角。∠4=∠1+∠2，∠4﹥∠1 ， ∠4﹥∠2三角形的外角性质： 由三角形内角和性质，我们还可以有以下两个结论：1、∠1＝800,∠2＝450,
则∠3＝ ； 312ABCDE试一试例2、一张小凳子的结构如图,∠1=∠2,
∠3=100°,求∠1的度数。∴∠3=∠1+∠2又∵∠1=∠2(三角形的一个外角等于和它不相邻的两个内角的和)解:∵∠3是△ABC的外角课内练习2
（1）三角形的任何一个外角大于和它不相邻的任意一个内角。
（2）四边形的内角和等于360度。明辨是非:１、在△ABC中∠A：∠B：∠C＝１：２：3，则 △ABC是（ ）A、锐角三角形 B、直角三角形
C、钝角三角形 D、不能确定２、已知△ABC中，∠A∶∠B∶∠C=2∶3∶4，求∠A、∠B和∠C的度数，它是什么三角形？（课内练习1）B随堂练习：3、在△ABC中，
（1）∠C=70°，∠A=50°，则∠B= 度；
（2）∠B=100°，∠A=∠C，则∠C= 度．6040 ５、如下左图，在 Rt△CDE,　∠C和∠E的关系是 ，其中∠C=55°，则∠E= 度互余356030６、如上右图， 在Rt△ABC中，∠A=2∠B，则∠A= 度，∠B= 度； 思考：如下图，要计算：∠A+∠B+∠C+∠D+∠E+∠F= 度BCDAGMHEF3601、三角形的内角和等于180°。
2、三角形的外角及其性质。
3、三角形按角分类。 在三角形的三个角中找出一个角是直角或是钝角，就能判定它是直角三角形或者是钝角三角形，但如果判定它是锐角三角形，就必须知道三个角都是锐角才行。小结下课了！
再见