二次函数专题复习

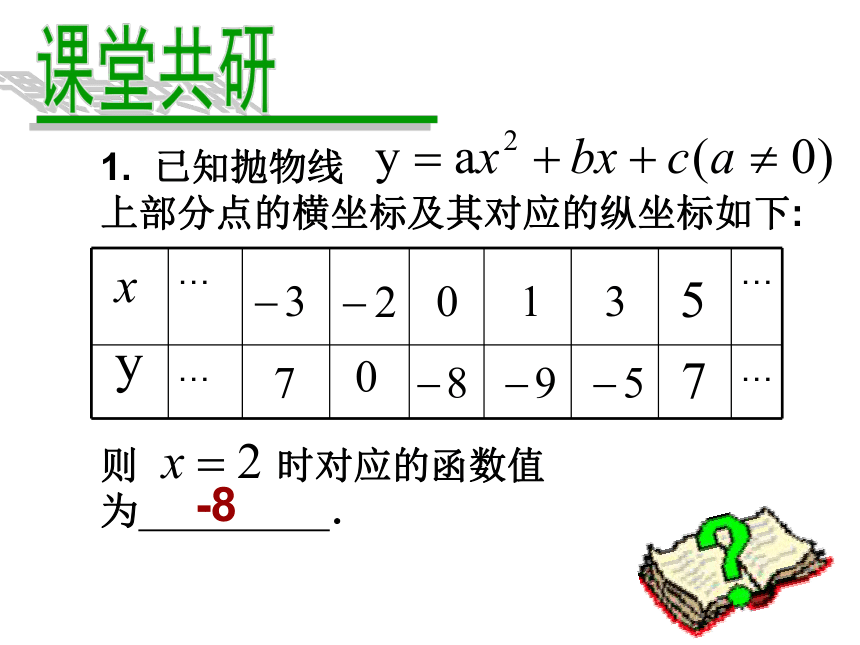
课件15张PPT。二次函数专题复习课前热身1. 已知二次函数
的图象经过点（- 4，10），（2，10）
和(1,0),则此二次函数的解析式
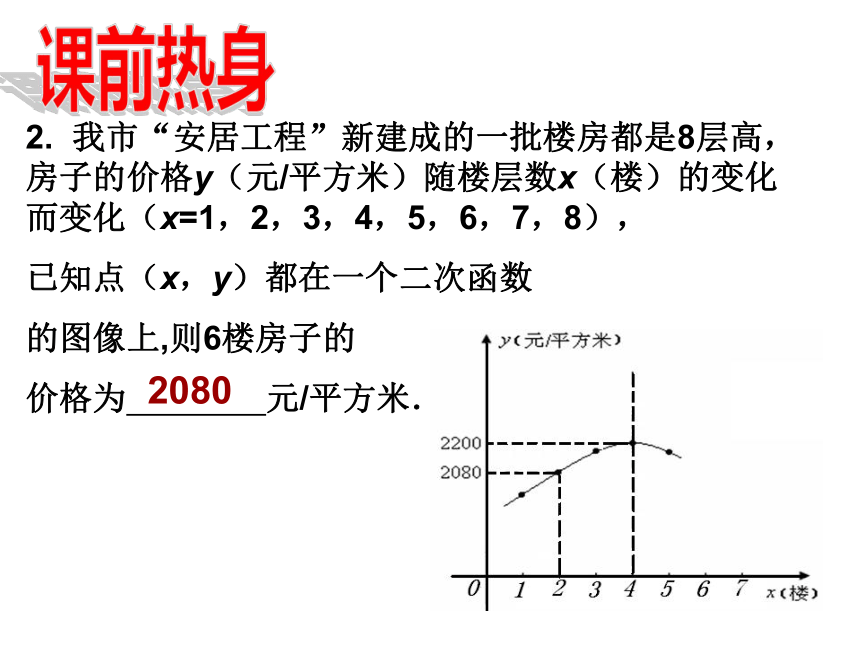
为 ．课前热身2. 我市“安居工程”新建成的一批楼房都是8层高，房子的价格y（元/平方米）随楼层数x（楼）的变化而变化（x=1，2，3，4，5，6，7，8），
已知点（x，y）都在一个二次函数
的图像上,则6楼房子的
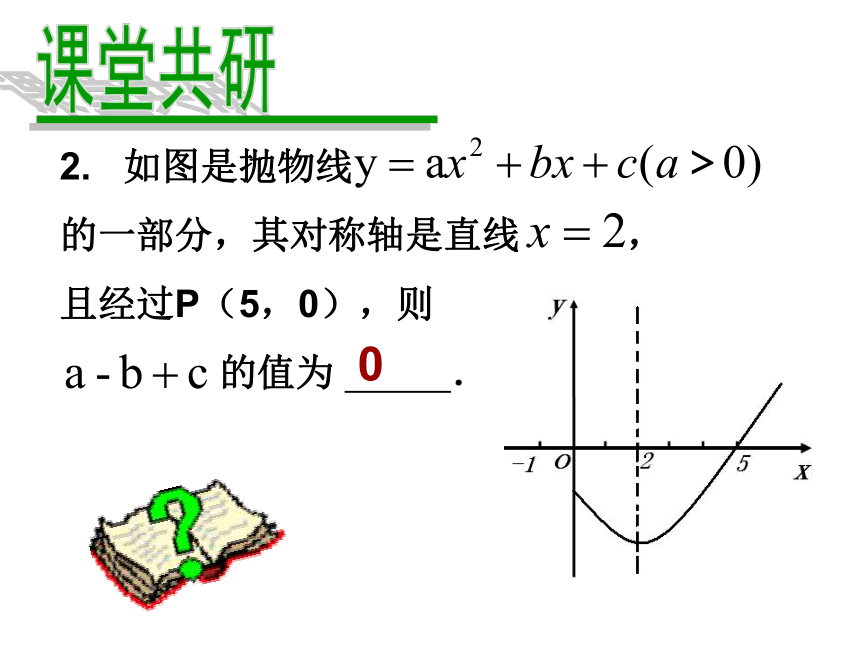
价格为 元/平方米． 2080-82. 如图是抛物线 　　　　　　　　
的一部分，其对称轴是直线 ，
且经过P（5，0），则
的值为 ．03. 已知抛物线 　　　　　　　　
经过三点A（2000，8），B（2008，2008），
C（2016，8），则它的顶点为 ．（2008，2008）已知抛物线 　　　　
经过A（4,2), B(5,7）两点，求抛物线
对称轴上一点P,使得 △PAB周长最小．(2008年宁波市)2． 已知二次函数中，函数与自变量的部分对应值如下表：（1）求该二次函数的关系式；
（2）若 ， 两点都在该

函数的图象上，试比较 与 的大小．(2008年南京市)如图，某隧道横截面的上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成，最大高度为6米，底部宽度为12米. 现以O点为原点，OM所在直线为x轴建立直角坐标系.
(1) 直接写出点M及抛物线顶点P的坐标；
(2) 求出这条抛物线的函数解析式；
(3) 若要搭建一个矩形“支撑架”AD- DC- CB，使C、D点在抛物线上，A、B点在地面OM上，则这个“支撑架”总长的最大值是多少？（2008佛山市）课前热身1. 已知点（1，4），（3，4）在二次函
数 　　　　　的图象上，则此
二次函数的顶点坐标为 ．