7.4一次函数的图象(1)

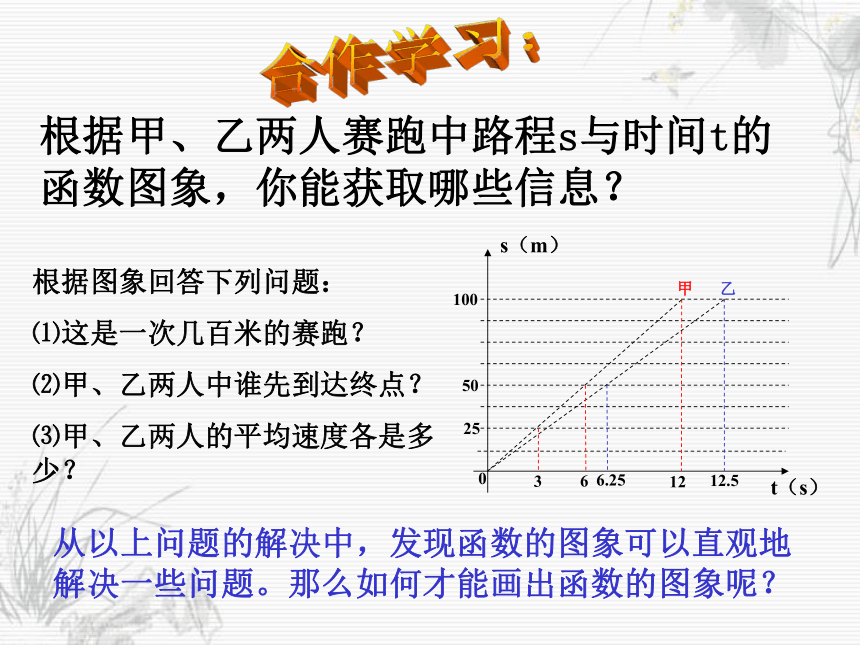
课件13张PPT。7.4一次函数的图象(1)根据甲、乙两人赛跑中路程s与时间t的函数图象，你能获取哪些信息？合作学习：根据图象回答下列问题：
⑴这是一次几百米的赛跑？
⑵甲、乙两人中谁先到达终点？
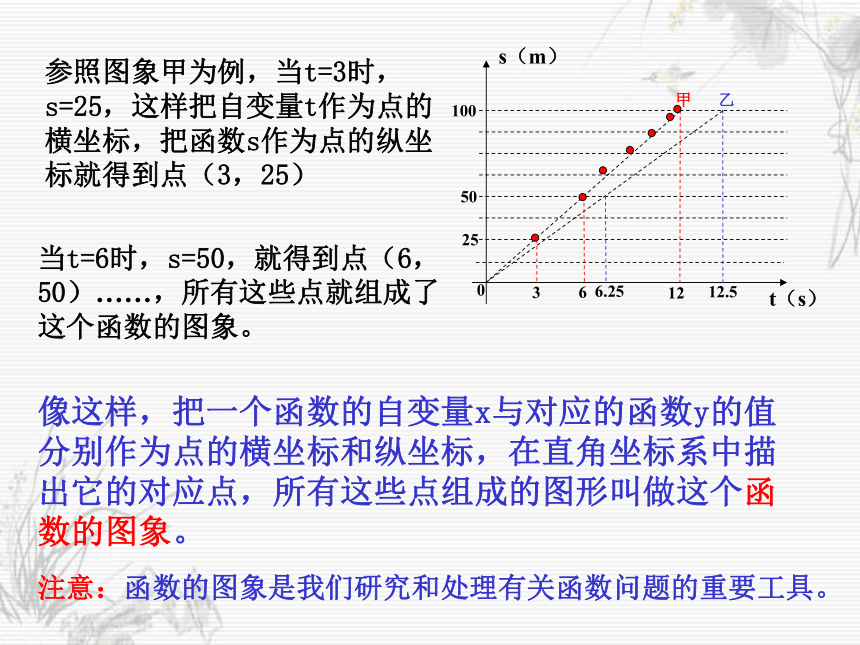
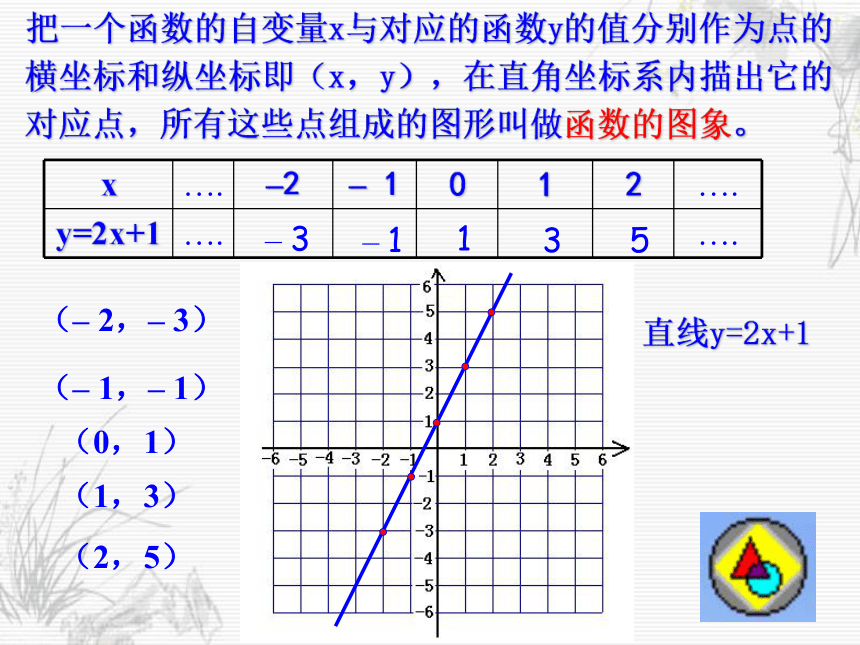
⑶甲、乙两人的平均速度各是多少？从以上问题的解决中，发现函数的图象可以直观地解决一些问题。那么如何才能画出函数的图象呢？参照图象甲为例，当t=3时，s=25，这样把自变量t作为点的横坐标，把函数s作为点的纵坐标就得到点（3，25）当t=6时，s=50，就得到点（6，50）……，所有这些点就组成了这个函数的图象。像这样，把一个函数的自变量x与对应的函数y的值分别作为点的横坐标和纵坐标，在直角坐标系中描出它的对应点，所有这些点组成的图形叫做这个函数的图象。注意：函数的图象是我们研究和处理有关函数问题的重要工具。把一个函数的自变量x与对应的函数y的值分别作为点的横坐标和纵坐标即（x，y），在直角坐标系内描出它的对应点，所有这些点组成的图形叫做函数的图象。– 3– 1135（– 2，– 3）（– 1，– 1）（0，1）（1，3）（2，5）直线y=2x+1例１：在同一坐标系作出下列函数的图象，
并求它们与坐标轴的交点坐标：
Y=3x, y=-3x+2请求一求这两条直线的交点坐标求直线与x轴交点坐标：令y=0
求直线与y轴交点坐标：令x=0例2：下列各点中，在直线y=2x－3上的是（ ）
（A）（0，3） （B）（1，1）
（C）（2，1） （D）（ －1，5）C例3：（1）若点（a，3）在直线y=2x－5上，则a=______（2）若点（2，－3）在直线y=kx+7上，则k=______4-5例4：已知一次函数的图象与坐标轴交与点（0，1），（1，0），求这个一次函数的解析式是____________ y = -x + 1例5：已知一次函数y=-2x+6。（1）求该函数的图象与坐标轴交点的坐标。（2）画出该函数的图象。例6：在同一直角坐标系中画出下列直线。梳理一下吧！ 1、函数图象的概念： 把一个函数的自变量x与对应的函数y的值分别作
为点的横坐标和纵坐标 , 在直角坐标系内描出它的对 应点 , 所有这些点组成的图形叫做该函数的图象. 2、函数图象的画法：描点法3、一次函数y=kx+b（k，b都是常数，且k≠0）的图象是一条直线，确定两点的坐标就可以画出一次函数图象。梳理一下吧！4、函数图象的概念包含两个方面的内容：
（1）满足函数解析式的任意一对x、y的值描出的点一定
在这个函数的图象上。
（2）反过来，在函数图象上的点（x，y）中的x、y一定满足函数的解析式。丰收园本节课你学到了什么?例6：在同一条道路上，甲每时走3km,出发0.15时后，乙以每时4.5km的速度追甲。设乙行走的时间为t(时)。 （1）写出甲、乙两同学每人所走的路程s与时t的关系；（2）在同一直角坐标系中画出它们的图象；（3）求出两条直线的交点坐标，并说明它们的实际意义；练一练1、函数y=2x+3的图象是（ ）
（A）过点（0，3），（0，- ）的直线。
（B）过点（0，- ），（1，5）的直线。
（C）过点（- ，0），（-1，1）的直线。
（D）过点（0，3），（ ，0）的直线。C2、已知函数y=-8x+16，求该函数图象与y轴的交点是（ ， ），与x轴的交点是（ ， ）；图象与坐标轴围成的三角形面积是（ ）016203、已知一次函数的图象与坐标轴交与点（0，1），（1，0），求这个一次函数的解析式是 （ ） y=-x+116试一试 已知直角坐标系中三点A（1，1），B（-1，3），C（3，-1）。这三点在同一直线上吗？请说明理由。解：设直线AB所对的一次函数为y=kx+b，
当x=1时，y=1； 当x=-1时，y=3代入
得 1=k+b
3=-k+b，
解得 k=-1，b=2
所以 函数解析式为 y=-x+2。
当x=3时，y =-x+2=-3+2=-1。
所以C在直线AB上，即A，B，C三点在同一直线上。