3.2 实数
图片预览





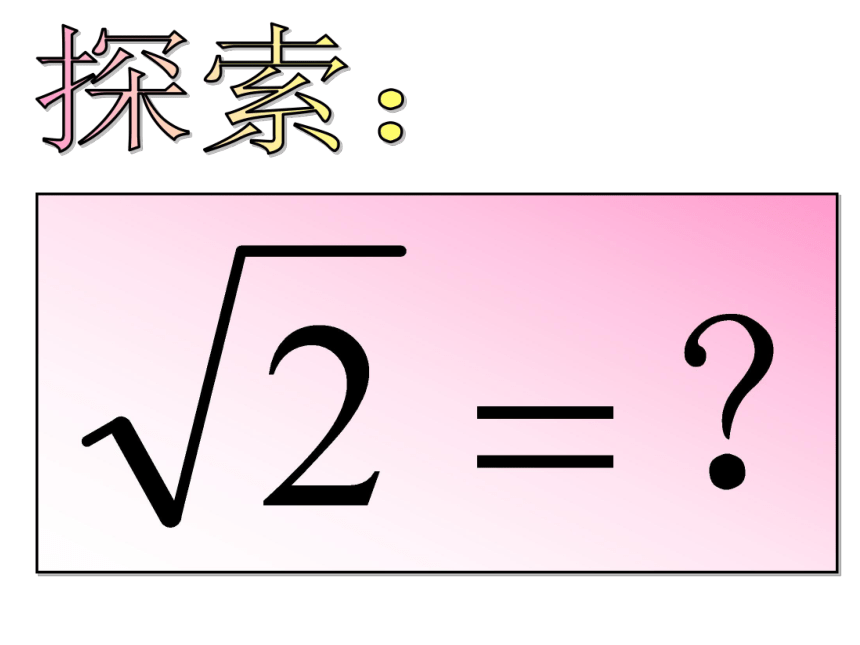



文档简介
课件40张PPT。实数复习回顾 想一想,昨天上课学习到了哪些知识,并试着将下面的填空题补充完整: 1、一个正数 有 个平方根,正平方根用 表示,负平方根用 表示.零的平方根等于 , 没有平方根.两零负数 2、正数的 平方根和 的平方根,统称算术平方根.一个数 的算术平方根记作 . 正零 是非题:
16的平方根是42 ( )
16的算术平方根是4 ( )
-4是16的平方根 ( )
16的平方根是4与-4 ( )
平方根等于本身的数1,0 ( )
算术平方根等于本身的数是1 ( )
-1的平方根是+1与-1 ( )
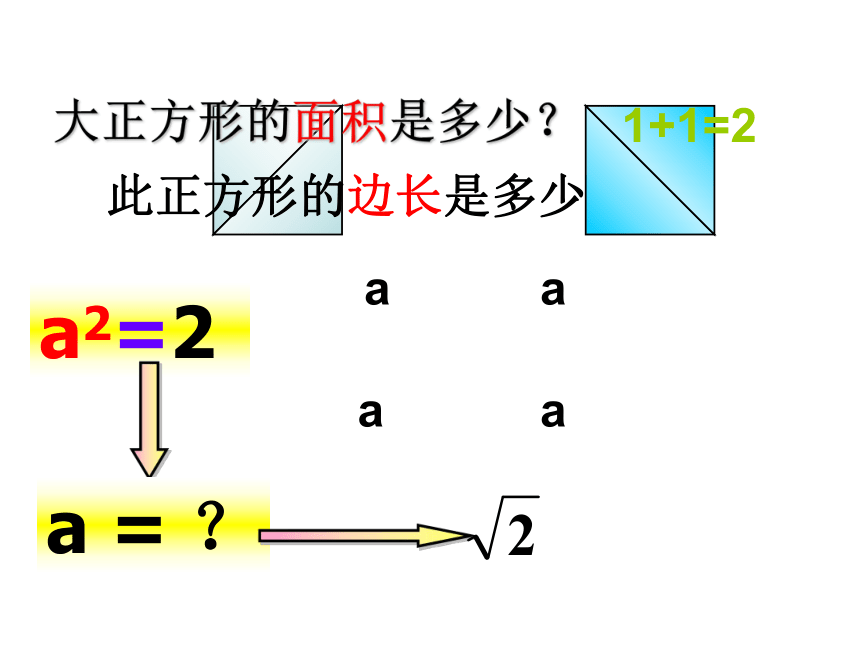
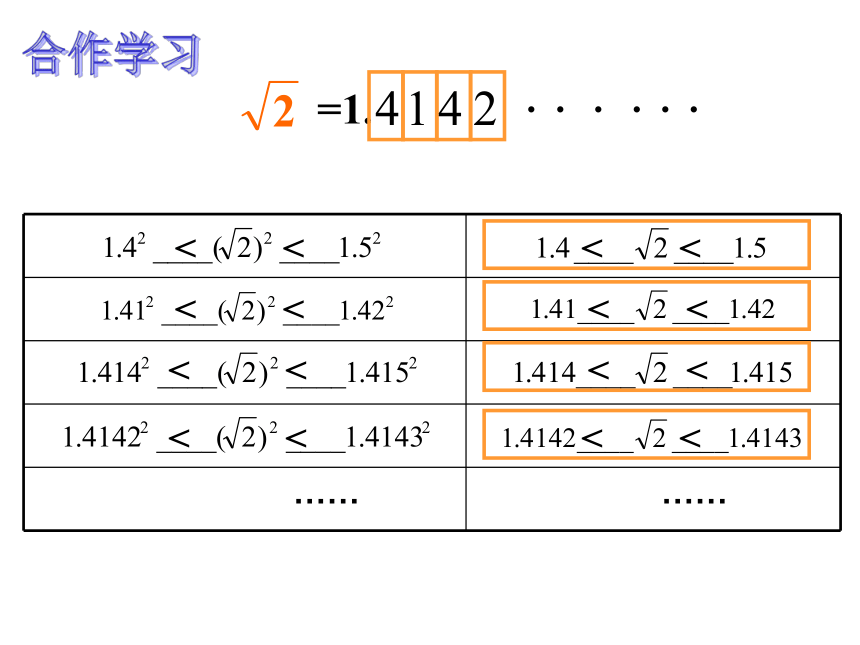
3的算术平方根记作3= ( )√×√√××××63把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形 剪一剪 拼一拼1111有理数能完全满足我们的生活需要吗? 大正方形的面积是多少? 1+1=2此正方形的边长是多少 aaaaa2=2a = ?探索:你能估计 的值在哪两个整数之间吗? 观察即 1< <2那么 到底是怎样一个数呢?=1. < << << << << << << << <. . . . . .合作学习 现在,科学家们利用超级计算机,将 精确地计算到了小数点后几亿位,但是也未能发现循环的情况,这说明 是一个无限的不循环的小数,它既不是整数,也不是分数。
所以, 不是有理数。 像 这种无限不循环小数,
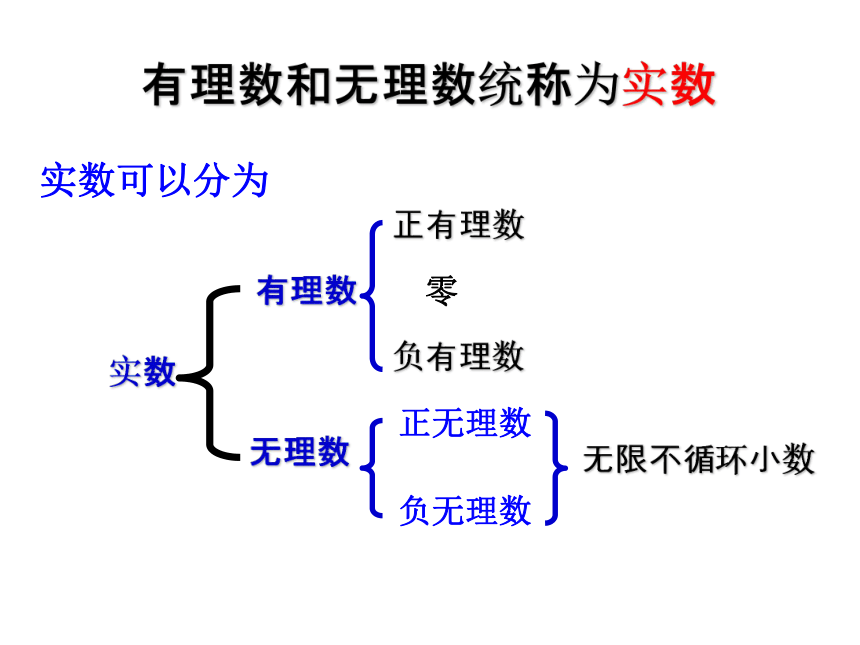
叫做无理数。有理数和无理数统称为实数实数可以分为 无理数就是无限的不循环
的小数。
还有哪些数是无理数呢?圆周率 及一些含有 的数都是无理数例如:像 的数是无理数。 想一想:凡是带有根号的数都是无理数吗?有一定的规律,但不循环的无限小数都是无理数。例如:
0.1010010001…〔两个1之间依次多1个0〕
-234.232232223…〔两个3之间依次多1个2〕0.12345678910111213 …〔小数部分有相继的正整数组成〕
无理数的三种类型:无理数广泛存在着,无理数一般有五种情况:①如 等,但 等是有理数;④1.010010001…(两个1之间依次多一个0),
95.6868868886…(两个6之间依次多一个8)等.③ 等;②.在
1.010010001…(两个“1”之间依次多1个0)中,
属于有理数的有:___________________
属于无理数的有:___________________1.010010001…(两个“1”之间依次多1个0)判断下列数哪些是有理数?哪些是无理数? 有理数是:
无理数是:
, , , ,议一议你能在数轴上准确表示 ?实数和数轴上的点是一一对应的。1 无理数和有理数一样,都可以表示在数轴上 !你能在数轴上表示 吗? 无理数和有理数一样,都可以表示在数轴上。也就是说实数都可以表示在数轴上。呢?一一对应每一个实数都可以用数轴上的一个点来表示。-2-1012实数 a实数数轴上的点 数轴上的每一个点都表示一个实数。例:把下列实数表示在数轴上,并比较它 们的大小(用“<”号连接)解:在数轴上表示如下。 -2 -1 0 1 2 3 4 5····1.53.3··-1.4(1)比较大小:
___ , ___ , ___ (2)将 , , , , , 从小到大的
顺序排列.(用“ ”连接)>
(1) 的相反数是__________
(2) 的相反数是
(3) ___________
(4)绝对值等于 的数是 _________ 填空题:
请任意说出三个无理数第一关第二关判断下列说法是否正确:1.无理数都是无限不循环小数。 ( )2.带根号的数都是无理数。 ( )3.无理数可以分为正无理数、0、负无理数。 ( )4.数轴上的任何一点都可以表示实数。 ( )第三关在下列各数中: , , ,
,0.12345…(小数部分由连续的正整数组成).无理数的个数有( ).
(A)6个 (B)5个 (C)4个 (D)3个D(1)在 中,
属于有理数的有:______________________;
属于无理数的有:_________________________;
属于实数的有:___________________________.注:把数从有理数扩充到实数以后,有理数中的
相反数和绝对值的概念同样适用于实数.(2) 的相反数是__________; 的相反数是__________.(3) ________; _________;(4)一个数的绝对值是 ,则这个数是______.在 (两个3之
间依次多一个0), 中,
①属于正数的有:__________________________;②属于无理数的有:________________________;③属于实数的有:__________________________;④上面无理数的相反数依次是:______________;⑤上面无理数的绝对值依次是:______________;⑥上面无理数用“<”号连接是:______________. 请将数轴上的点与下列实数对应起来.
CABDA ( ); B ( );
C ( ); D ( ); 探究学习 判断下列说法是否正确,并举例说明理由.
①两个无理数的和一定是无理数;
②两个无理数的积一定是无理数;
③两个无理数的商可能是有理数. 说说本节课的收获知识回顾:实数 :概念、范围分类、绝对值、相反数等数轴:数轴上的点与实数、比较大小等无理数 :概念、三种类型:探讨 的存在和大小拓展再提高变一变再变一变1、若5a+1和-4都是正数m的平方根,试求a和m的值。若实数x、y满足
求2x+y的值.-2 -1 0 1 2 3 4 5试一试:
你能在数轴上表示出 吗? 公元前6世纪,有个数学权威叫毕达哥拉斯,他曾断言,任何两条线段相比都可以用两个整数之比来表示,由此推导出自然界只有整数和分数两种数,不存在其他的数。但毕达哥拉斯这个结论提出不久,他的学生希伯斯就发现,边长为1的正方形,其对角线和边长不能成为整数比,既不是整数,又不是分数,而是一个当时人们还未认识的数。希伯斯的发现触犯了毕达哥拉斯的权威,于是,毕达哥拉斯就下令封锁这个发现,不让其传播。可是,希伯斯的发现还是不径而走,越来越多的人知道了这个新数。毕达哥拉斯大为恼怒,就下令追捕希伯斯,最后在一条船上找到了希伯斯,竟残忍的把他手脚捆住,扔进波涛汹涌的地中海。
希伯斯虽然葬身鱼腹,冤沉大海。但他的发现却为举世公认。这种新数如同圆周率∏一样,在自然界大量客观的存在着,于是人们将它取名为无理数。而无理数的无理并非没有道理的意思,而是为不可比的意思。无理二字在数学史上有可能是毕达哥拉斯为维护神权迫害数学人才的无理。但是毕达哥拉斯学派毕竟发现了新数,这引起了所谓数学史上的第一次危机,建立了无理数,扩大了数域,为数学发展作出了巨大的贡献。数学故事:无理数的发现
16的平方根是42 ( )
16的算术平方根是4 ( )
-4是16的平方根 ( )
16的平方根是4与-4 ( )
平方根等于本身的数1,0 ( )
算术平方根等于本身的数是1 ( )
-1的平方根是+1与-1 ( )
3的算术平方根记作3= ( )√×√√××××63把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形 剪一剪 拼一拼1111有理数能完全满足我们的生活需要吗? 大正方形的面积是多少? 1+1=2此正方形的边长是多少 aaaaa2=2a = ?探索:你能估计 的值在哪两个整数之间吗? 观察即 1< <2那么 到底是怎样一个数呢?=1. < << << << << << << << <. . . . . .合作学习 现在,科学家们利用超级计算机,将 精确地计算到了小数点后几亿位,但是也未能发现循环的情况,这说明 是一个无限的不循环的小数,它既不是整数,也不是分数。
所以, 不是有理数。 像 这种无限不循环小数,
叫做无理数。有理数和无理数统称为实数实数可以分为 无理数就是无限的不循环
的小数。
还有哪些数是无理数呢?圆周率 及一些含有 的数都是无理数例如:像 的数是无理数。 想一想:凡是带有根号的数都是无理数吗?有一定的规律,但不循环的无限小数都是无理数。例如:
0.1010010001…〔两个1之间依次多1个0〕
-234.232232223…〔两个3之间依次多1个2〕0.12345678910111213 …〔小数部分有相继的正整数组成〕
无理数的三种类型:无理数广泛存在着,无理数一般有五种情况:①如 等,但 等是有理数;④1.010010001…(两个1之间依次多一个0),
95.6868868886…(两个6之间依次多一个8)等.③ 等;②.在
1.010010001…(两个“1”之间依次多1个0)中,
属于有理数的有:___________________
属于无理数的有:___________________1.010010001…(两个“1”之间依次多1个0)判断下列数哪些是有理数?哪些是无理数? 有理数是:
无理数是:
, , , ,议一议你能在数轴上准确表示 ?实数和数轴上的点是一一对应的。1 无理数和有理数一样,都可以表示在数轴上 !你能在数轴上表示 吗? 无理数和有理数一样,都可以表示在数轴上。也就是说实数都可以表示在数轴上。呢?一一对应每一个实数都可以用数轴上的一个点来表示。-2-1012实数 a实数数轴上的点 数轴上的每一个点都表示一个实数。例:把下列实数表示在数轴上,并比较它 们的大小(用“<”号连接)解:在数轴上表示如下。 -2 -1 0 1 2 3 4 5····1.53.3··-1.4(1)比较大小:
___ , ___ , ___ (2)将 , , , , , 从小到大的
顺序排列.(用“ ”连接)>
(1) 的相反数是__________
(2) 的相反数是
(3) ___________
(4)绝对值等于 的数是 _________ 填空题:
请任意说出三个无理数第一关第二关判断下列说法是否正确:1.无理数都是无限不循环小数。 ( )2.带根号的数都是无理数。 ( )3.无理数可以分为正无理数、0、负无理数。 ( )4.数轴上的任何一点都可以表示实数。 ( )第三关在下列各数中: , , ,
,0.12345…(小数部分由连续的正整数组成).无理数的个数有( ).
(A)6个 (B)5个 (C)4个 (D)3个D(1)在 中,
属于有理数的有:______________________;
属于无理数的有:_________________________;
属于实数的有:___________________________.注:把数从有理数扩充到实数以后,有理数中的
相反数和绝对值的概念同样适用于实数.(2) 的相反数是__________; 的相反数是__________.(3) ________; _________;(4)一个数的绝对值是 ,则这个数是______.在 (两个3之
间依次多一个0), 中,
①属于正数的有:__________________________;②属于无理数的有:________________________;③属于实数的有:__________________________;④上面无理数的相反数依次是:______________;⑤上面无理数的绝对值依次是:______________;⑥上面无理数用“<”号连接是:______________. 请将数轴上的点与下列实数对应起来.
CABDA ( ); B ( );
C ( ); D ( ); 探究学习 判断下列说法是否正确,并举例说明理由.
①两个无理数的和一定是无理数;
②两个无理数的积一定是无理数;
③两个无理数的商可能是有理数. 说说本节课的收获知识回顾:实数 :概念、范围分类、绝对值、相反数等数轴:数轴上的点与实数、比较大小等无理数 :概念、三种类型:探讨 的存在和大小拓展再提高变一变再变一变1、若5a+1和-4都是正数m的平方根,试求a和m的值。若实数x、y满足
求2x+y的值.-2 -1 0 1 2 3 4 5试一试:
你能在数轴上表示出 吗? 公元前6世纪,有个数学权威叫毕达哥拉斯,他曾断言,任何两条线段相比都可以用两个整数之比来表示,由此推导出自然界只有整数和分数两种数,不存在其他的数。但毕达哥拉斯这个结论提出不久,他的学生希伯斯就发现,边长为1的正方形,其对角线和边长不能成为整数比,既不是整数,又不是分数,而是一个当时人们还未认识的数。希伯斯的发现触犯了毕达哥拉斯的权威,于是,毕达哥拉斯就下令封锁这个发现,不让其传播。可是,希伯斯的发现还是不径而走,越来越多的人知道了这个新数。毕达哥拉斯大为恼怒,就下令追捕希伯斯,最后在一条船上找到了希伯斯,竟残忍的把他手脚捆住,扔进波涛汹涌的地中海。
希伯斯虽然葬身鱼腹,冤沉大海。但他的发现却为举世公认。这种新数如同圆周率∏一样,在自然界大量客观的存在着,于是人们将它取名为无理数。而无理数的无理并非没有道理的意思,而是为不可比的意思。无理二字在数学史上有可能是毕达哥拉斯为维护神权迫害数学人才的无理。但是毕达哥拉斯学派毕竟发现了新数,这引起了所谓数学史上的第一次危机,建立了无理数,扩大了数域,为数学发展作出了巨大的贡献。数学故事:无理数的发现
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
