第三章圆的基本性质单元复习(二课时)
图片预览




文档简介
(共35张PPT)
第三章圆单元复习
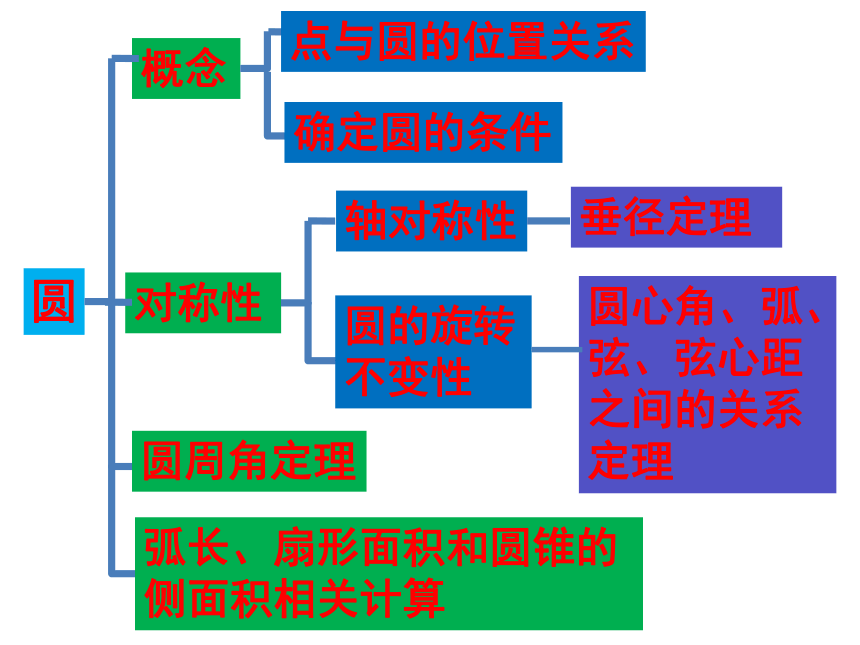
圆
概念
对称性
圆周角定理
点与圆的位置关系
确定圆的条件
轴对称性
圆的旋转不变性
垂径定理
圆心角、弧、弦、弦心距之间的关系定理
弧长、扇形面积和圆锥的侧面积相关计算
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫做圆。
圆的定义
固定的端点O叫做圆心,线段OA叫做半径,以点O为圆心的圆,记作☉O,读作“圆O”
半径确定圆的大小;圆心确定圆的位置
圆是一条封闭曲线
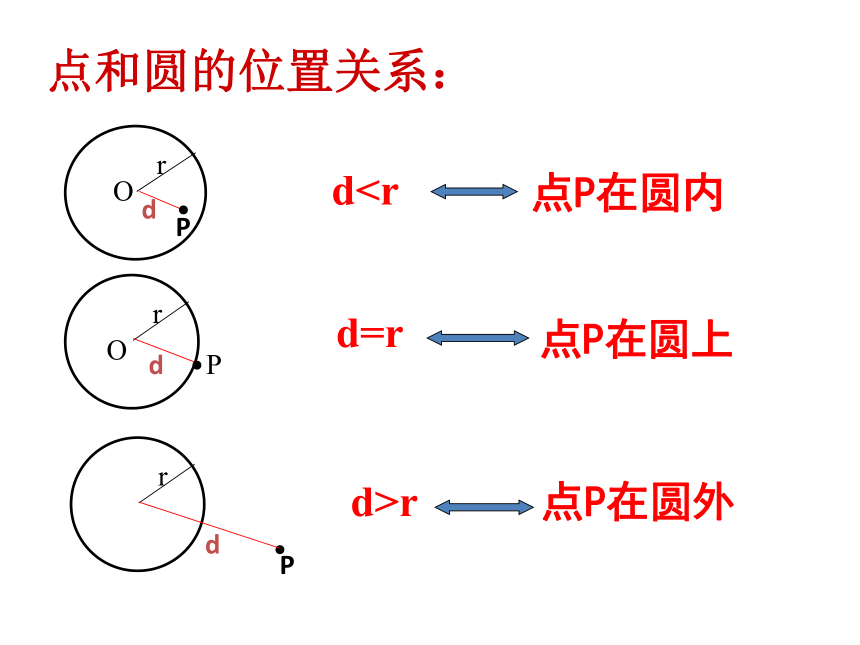
d点P在圆内
d=r
点P在圆上
d>r
点P在圆外
点和圆的位置关系:
r
O
P
●
d
●
r
P
d
r
O
●
P
d
1、⊙O的半径为13cm,圆心O到直线的距离OD=5cm.在直线上有三点P,Q,R,且PD = 12cm , QD<12cm, RD>12cm,则点P在 ,点Q在 ,点R在 .
圆上
圆内
圆外
3或7cm
3、已知Rt⊿ABC,∠ACB=90°AC=3,BC=4,M是
AB的中点,以C为圆心,以2.5为半径作圆,则点A,B,C,M与圆的位置关系
2、一个点到圆的最小距离为4cm,最大距离为10cm,则该圆的半径是 。
做一做
∠C=90°
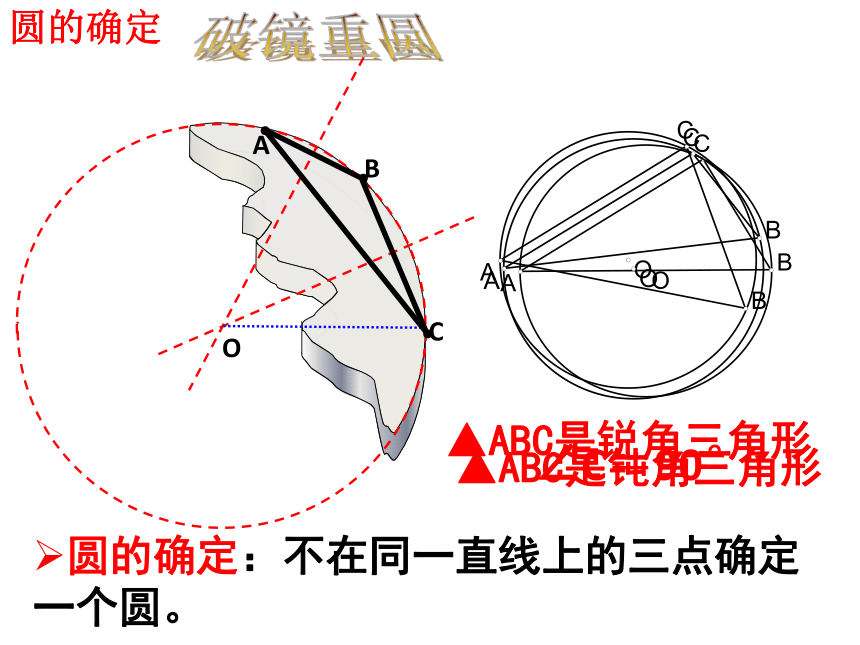
▲ABC是锐角三角形
▲ABC是钝角三角形
圆的确定:不在同一直线上的三点确定一个圆。
圆的确定
O
A
C
B
破镜重圆
●
●
●
2.过两点的圆有_________个,这些圆的圆心的都在 上.
过三点的圆及外接圆
1.过一点的圆有________个
无数
无数
0或1
连结着两点的线段的垂直平分线
4.如何作过不在同一直线上的三点的圆(或三角形的外接圆、找外心、破镜重圆、到三个村庄距离相等)
3.过三点的圆有______________个
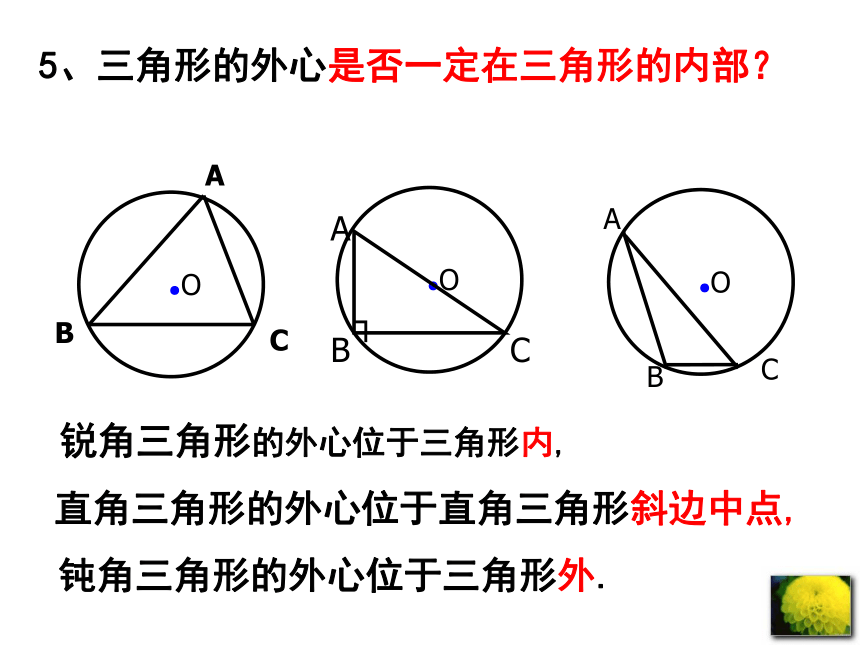
锐角三角形的外心位于三角形内,
●O
A
B
C
●O
5、三角形的外心是否一定在三角形的内部?
A
B
C
C
A
B
┐
●O
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
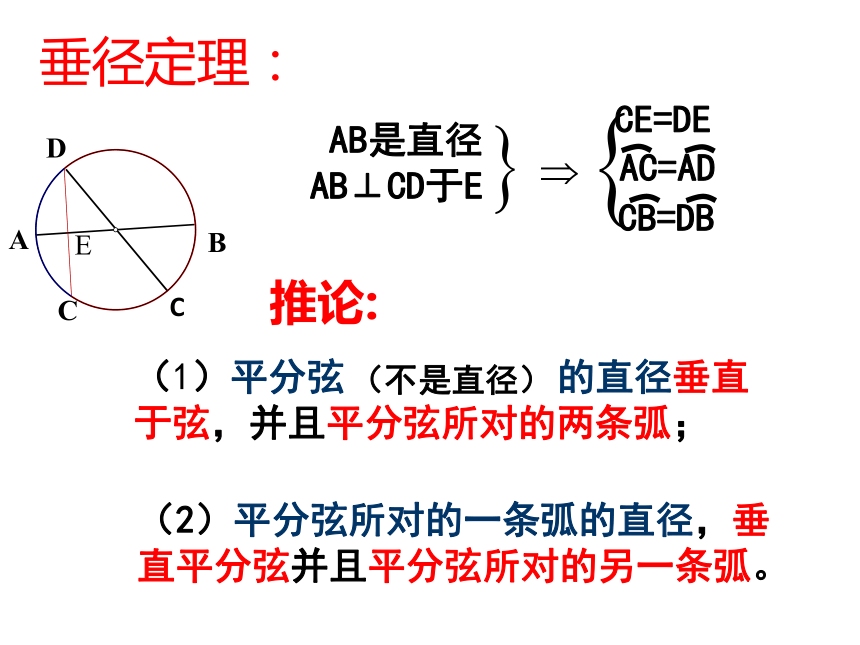
AB是直径
AB⊥CD于E
垂径定理:
CB=DB
AC=AD
CE=DE
E
D
B
A
C
C
推论:
(2)平分弦所对的一条弧的直径,垂直平分弦并且平分弦所对的另一条弧。
(1)平分弦 的直径垂直于弦,并且平分弦所对的两条弧;
(不是直径)
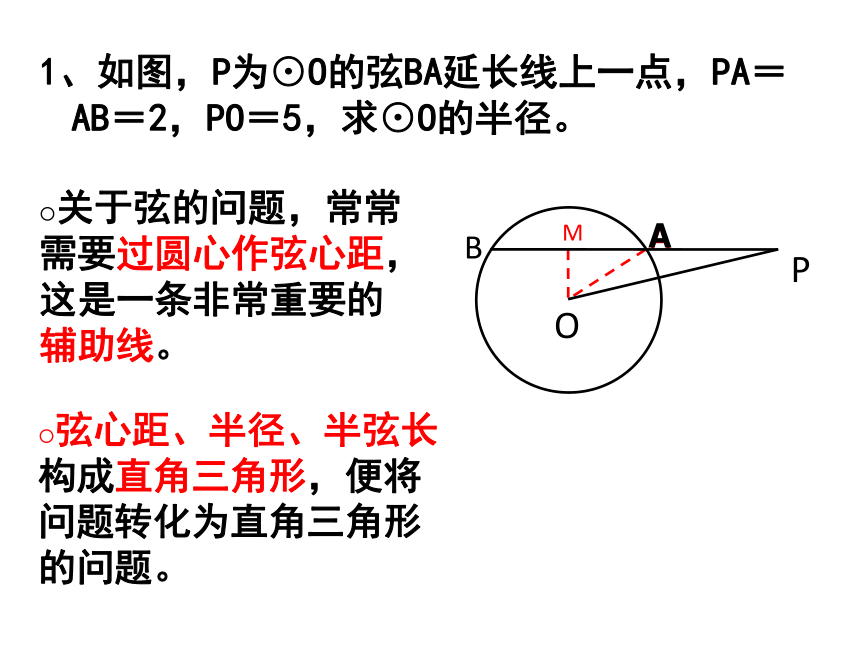
1、如图,P为⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径。
M
A
P
B
O
A
关于弦的问题,常常需要过圆心作弦心距,这是一条非常重要的辅助线。
弦心距、半径、半弦长构成直角三角形,便将问题转化为直角三角形的问题。
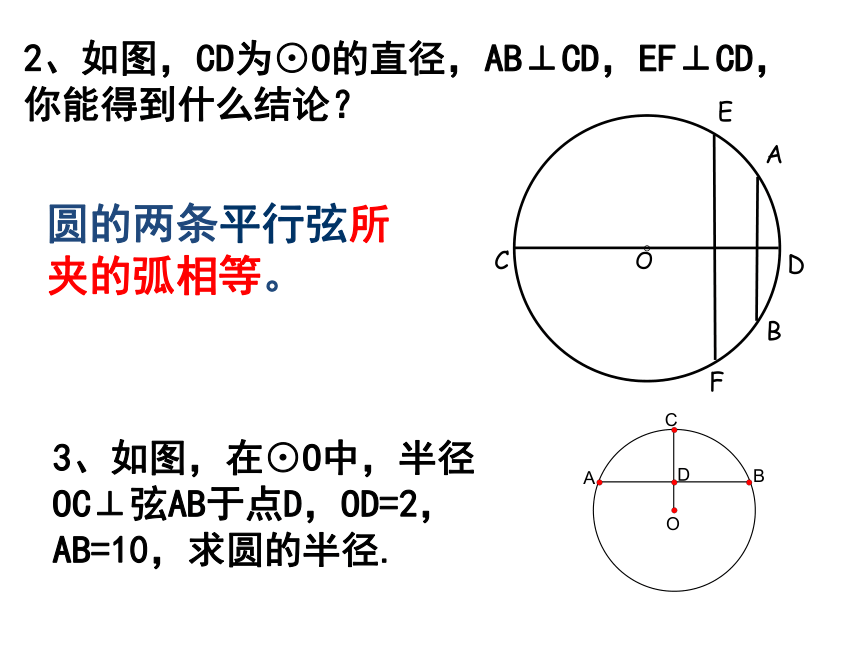
2、如图,CD为⊙O的直径,AB⊥CD,EF⊥CD,你能得到什么结论?
F
O
B
A
E
C
D
圆的两条平行弦所夹的弧相等。
3、如图,在⊙O中,半径OC⊥弦AB于点D,OD=2,AB=10,求圆的半径.
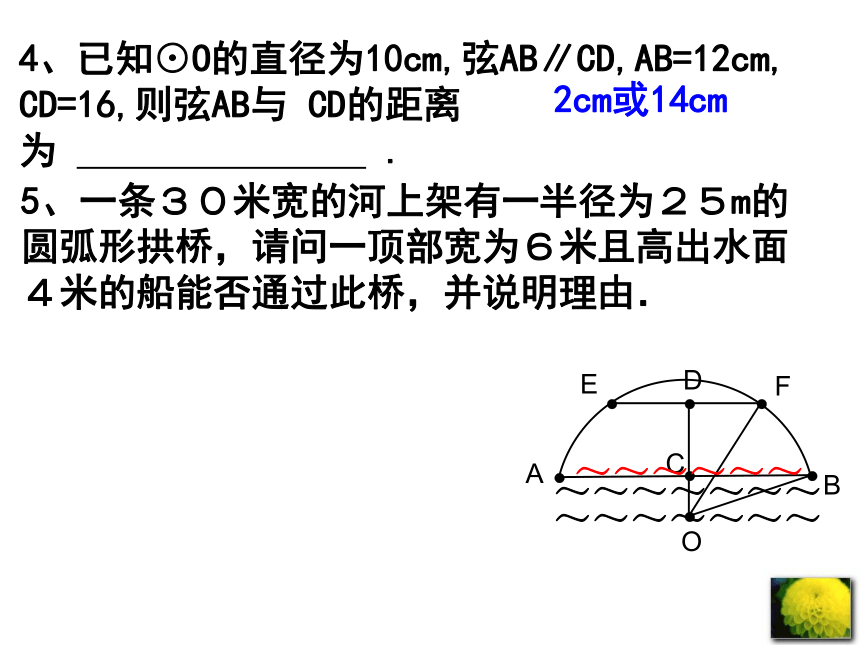
4、已知⊙O的直径为10cm,弦AB∥CD,AB=12cm,
CD=16,则弦AB与 CD的距离为 .
2cm或14cm
5、一条30米宽的河上架有一半径为25m的圆弧形拱桥,请问一顶部宽为6米且高出水面4米的船能否通过此桥,并说明理由.
~~~~~~
~~~~~~~
~~~~~~~
圆的旋转不变性
圆心角定理
圆心角所对的弧相等, 圆心角所对的弦相等, 圆心角所对弦的弦心距相等。
在同圆或等圆 (前提)
圆心角相等
(条件)
推论 在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等。
一条弧所对的圆周角等于它所对的圆心角的一半。
圆周角定理
也可以理解为:一条弧所对的圆心角是它所对的圆周角的二倍;圆周角的度数等于它所对的弧的度数的一半。
推论1 同圆或等圆中,同弧或等弧所对的圆周角相等; 相等的圆周角所对的弧相等
推论2 半圆(或直径)所对的圆周角是90°;90°的圆周角所对的弦是直径。
1、如图,四边形ABCD内接于⊙O,若∠BOD=140°,则∠BCD等于( )
A.140° B.110° C.70° D.20 °
B
2、如图,AD是△ABC的外接圆直径,
AD= ∠B=∠DAC,则AC的长为( )
2 B.
C.1 D. 不能确定
C
3、如图,AB是⊙ O 的直径,C,D,E都是⊙O 上的点,则∠1+∠2= .
2
90°
1
2
4、如图,CD是⊙ O 的直径, O是圆心,E是圆上一点,且∠EOD=45°,A是DC延长线上一点,AE与半圆交于一点B,AB=OC,则∠EAD= .
15°
6、如图,在⊙O中,DE=2BC, ∠ EOD=64°,求∠ A的度数。
︵
︵
A
B
C
D
E
O
若BC=n°,DE=m°呢
︵
︵
5、 在⊙O中,弦AB所对的圆心角
∠AOB=100°,则弦AB所对的圆周角为______.
500或1300
7、如图,在⊙O中,DE=2BC=64°,
求∠E AD的度数。
︵
︵
m
A
B
C
D
E
若BC=n°,DE=m°呢
︵
︵
8、如图:圆O中弦AB等于半径R,则这条弦所对的圆心角是___,圆周角是______.
60度
30度或150度
9、如图,△ABC是等边三角形,以BC为直径画⊙O交AB,AC于D,E 求证:BD=CE
10、如图, ⊙O 的直径PQ⊥弦CD,AC=BD,PQ交弦AB于点E.
求证:AE=BE
⌒
⌒
O
A
B
C
D
E
P
Q
11、P是⊙O直径AB上一点,PC⊥AB,PC交⊙O于C,∠OCP的平分线交⊙O于D,当点P在半径OA(包括0点,但不包括A点)上移动时,试比较弧AD和弧BD的大小,并证明你的结论。
A
B
C
D
P
0
M
G
1.弧长公式:
2.扇形面积公式:
3.圆锥侧面积公式:
4.圆锥全面积公式:
5.圆锥侧面展开图扇形圆心角公式:
计算公式:
1.已知弧长为4πcm,它所对的圆心角为120°,那么它所对的弦长为( )
2.在⊙O中, 所对的圆心角为60°,且弦AB=5cm,则 的长为( )
C
A
做一做
3、如图,在扇形OAB中,∠AOB=90°,已以AB为直径画半圆,则阴影部分面积是( )
A.大于S△AOB B.等于S △AOB
C.小于S △AOB D.不能确定与S △AOB的关系
4.如图,正方形的边长为2,以边长为直径在正方形内画半圆,则阴影部分面积是( )
A.π- 4 B. 4- π C.π- 2 D.4- π/4
B
B
5.一个形如圆锥的冰淇淋纸筒,其底面直径为6cm,母线长5cm,则它的侧面积是( )
A.66π B.30π C.28π D.15π
6.在半径为6cm的圆中,120°的圆心角所对的弧长为 .
7.扇形半径为12,面积为9π,它的圆心角等于 度
D
4πcm
22.5
8.已知扇形的面积为24π ,弧长为8πcm,则扇形的半径是 cm,圆心角是 度
6
240
9.已知扇形的面积是12 ,半径是8cm,则扇形周长是 .
10.圆锥的底面半径是1cm,母线是2cm,则高是 cm,侧面积是 ,全面积是 。
19
2π
3π
11、如图,在⊙O中,弦AC=2cm,圆周角∠ABC=45°求阴影部分面积
12、如图,把Rt△ABC的斜边放在直线 l 上,按顺时针方向在 l 上转动2次,使它转到△A2B2C2的位置.设BC=1,AC=
求(1)点A所经过的路线长.
(2)点A所经过的路线与直线l所围成的面积.
13、如图,已知扇AOB,∠AOB=90°,OA=OB=4,以OA为直径作半圆⊙M,作MP∥OB交AB于P,交⊙M于点Q,求阴影部分面积.
14、一个圆锥的侧面展开图是半径为18cm,圆心角为2400的扇形,求这个圆锥的高。
15、下图是由直径分别为4cm,6cm和10cm的三个半圆所组成的图形,求图中阴影部分的周长和面积。
16、如图,一个圆锥的高为 cm,侧面展开图是半圆,求
(1)圆锥母线l与底面半径之比.
(2)圆锥的表面积.
17、巳知圆锥的轴截面周长为10cm,设腰长为x,圆锥的表面积为S,求: ⑴ S关于X的函数表达式和自变量X的取值范围; ⑵ 画出这个函数图象,确定S的取值范围
例题解析:
1、我国某些东南沿海地区常会受到台风的侵袭,某日A市气象台测得台风中心在A市正东方向400km的B处,正快速向西北方向运动,距台风中心300km的范围内将受到影响,问A市是否会受到这次台风的影响?为什么?
A
B
D
东
北
C
2、如图,P1是一块半径为1的半圆纸板,在P1的左下角剪去一个半径为 的半圆后,得到图形P2,然后依次剪去一个更小的半圆(其直径为前一个被剪去半圆的半径)得到图形P3,P4,P5…,Pn,…,记纸板Pn的面积为Sn,试计算求出S2 ,S3 ,并猜测得到Sn-Sn-1= ,(n≥2)。
P1
P2
P3
P4
3、如图,已知⊙O的半径为5,点O到弦AB的距离为3,则⊙O上到弦AB所在直线的距离为2的点有( )个。
A、1 B、2 C、3 D、4
4、如图,⊙C经过原点且与坐标轴分别交于点A与点B,点A的坐标为(0,4),M是圆上一点,∠BMO=120°,求⊙C的半径和圆心C的坐标。
A
B
C
M
O
X
Y
D
G
5、已知P(x,y)是以坐标原点为圆心,5为半径的圆周上的点,若x,y都是整数,则这样的点共有( )个。
A、4 B、8 C、12 D、16
6、钟表的轴心到分针针端的长为5cm,若经过40min,求分针针端转过的弧长。
7、如图,有一块圆形铁皮,BC是⊙O的直径,AB=AC,在此圆形铁皮中剪下一个扇形(阴影部分)。
(1)当⊙O的半径为2时,求这个扇形(阴影部分)的面积(结果保留π)
(2)当O的半径为R0(R0>2)时,在剩下的三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由。
A
B
C
E
F
O
第三章圆单元复习
圆
概念
对称性
圆周角定理
点与圆的位置关系
确定圆的条件
轴对称性
圆的旋转不变性
垂径定理
圆心角、弧、弦、弦心距之间的关系定理
弧长、扇形面积和圆锥的侧面积相关计算
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫做圆。
圆的定义
固定的端点O叫做圆心,线段OA叫做半径,以点O为圆心的圆,记作☉O,读作“圆O”
半径确定圆的大小;圆心确定圆的位置
圆是一条封闭曲线
d
d=r
点P在圆上
d>r
点P在圆外
点和圆的位置关系:
r
O
P
●
d
●
r
P
d
r
O
●
P
d
1、⊙O的半径为13cm,圆心O到直线的距离OD=5cm.在直线上有三点P,Q,R,且PD = 12cm , QD<12cm, RD>12cm,则点P在 ,点Q在 ,点R在 .
圆上
圆内
圆外
3或7cm
3、已知Rt⊿ABC,∠ACB=90°AC=3,BC=4,M是
AB的中点,以C为圆心,以2.5为半径作圆,则点A,B,C,M与圆的位置关系
2、一个点到圆的最小距离为4cm,最大距离为10cm,则该圆的半径是 。
做一做
∠C=90°
▲ABC是锐角三角形
▲ABC是钝角三角形
圆的确定:不在同一直线上的三点确定一个圆。
圆的确定
O
A
C
B
破镜重圆
●
●
●
2.过两点的圆有_________个,这些圆的圆心的都在 上.
过三点的圆及外接圆
1.过一点的圆有________个
无数
无数
0或1
连结着两点的线段的垂直平分线
4.如何作过不在同一直线上的三点的圆(或三角形的外接圆、找外心、破镜重圆、到三个村庄距离相等)
3.过三点的圆有______________个
锐角三角形的外心位于三角形内,
●O
A
B
C
●O
5、三角形的外心是否一定在三角形的内部?
A
B
C
C
A
B
┐
●O
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
AB是直径
AB⊥CD于E
垂径定理:
CB=DB
AC=AD
CE=DE
E
D
B
A
C
C
推论:
(2)平分弦所对的一条弧的直径,垂直平分弦并且平分弦所对的另一条弧。
(1)平分弦 的直径垂直于弦,并且平分弦所对的两条弧;
(不是直径)
1、如图,P为⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径。
M
A
P
B
O
A
关于弦的问题,常常需要过圆心作弦心距,这是一条非常重要的辅助线。
弦心距、半径、半弦长构成直角三角形,便将问题转化为直角三角形的问题。
2、如图,CD为⊙O的直径,AB⊥CD,EF⊥CD,你能得到什么结论?
F
O
B
A
E
C
D
圆的两条平行弦所夹的弧相等。
3、如图,在⊙O中,半径OC⊥弦AB于点D,OD=2,AB=10,求圆的半径.
4、已知⊙O的直径为10cm,弦AB∥CD,AB=12cm,
CD=16,则弦AB与 CD的距离为 .
2cm或14cm
5、一条30米宽的河上架有一半径为25m的圆弧形拱桥,请问一顶部宽为6米且高出水面4米的船能否通过此桥,并说明理由.
~~~~~~
~~~~~~~
~~~~~~~
圆的旋转不变性
圆心角定理
圆心角所对的弧相等, 圆心角所对的弦相等, 圆心角所对弦的弦心距相等。
在同圆或等圆 (前提)
圆心角相等
(条件)
推论 在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等。
一条弧所对的圆周角等于它所对的圆心角的一半。
圆周角定理
也可以理解为:一条弧所对的圆心角是它所对的圆周角的二倍;圆周角的度数等于它所对的弧的度数的一半。
推论1 同圆或等圆中,同弧或等弧所对的圆周角相等; 相等的圆周角所对的弧相等
推论2 半圆(或直径)所对的圆周角是90°;90°的圆周角所对的弦是直径。
1、如图,四边形ABCD内接于⊙O,若∠BOD=140°,则∠BCD等于( )
A.140° B.110° C.70° D.20 °
B
2、如图,AD是△ABC的外接圆直径,
AD= ∠B=∠DAC,则AC的长为( )
2 B.
C.1 D. 不能确定
C
3、如图,AB是⊙ O 的直径,C,D,E都是⊙O 上的点,则∠1+∠2= .
2
90°
1
2
4、如图,CD是⊙ O 的直径, O是圆心,E是圆上一点,且∠EOD=45°,A是DC延长线上一点,AE与半圆交于一点B,AB=OC,则∠EAD= .
15°
6、如图,在⊙O中,DE=2BC, ∠ EOD=64°,求∠ A的度数。
︵
︵
A
B
C
D
E
O
若BC=n°,DE=m°呢
︵
︵
5、 在⊙O中,弦AB所对的圆心角
∠AOB=100°,则弦AB所对的圆周角为______.
500或1300
7、如图,在⊙O中,DE=2BC=64°,
求∠E AD的度数。
︵
︵
m
A
B
C
D
E
若BC=n°,DE=m°呢
︵
︵
8、如图:圆O中弦AB等于半径R,则这条弦所对的圆心角是___,圆周角是______.
60度
30度或150度
9、如图,△ABC是等边三角形,以BC为直径画⊙O交AB,AC于D,E 求证:BD=CE
10、如图, ⊙O 的直径PQ⊥弦CD,AC=BD,PQ交弦AB于点E.
求证:AE=BE
⌒
⌒
O
A
B
C
D
E
P
Q
11、P是⊙O直径AB上一点,PC⊥AB,PC交⊙O于C,∠OCP的平分线交⊙O于D,当点P在半径OA(包括0点,但不包括A点)上移动时,试比较弧AD和弧BD的大小,并证明你的结论。
A
B
C
D
P
0
M
G
1.弧长公式:
2.扇形面积公式:
3.圆锥侧面积公式:
4.圆锥全面积公式:
5.圆锥侧面展开图扇形圆心角公式:
计算公式:
1.已知弧长为4πcm,它所对的圆心角为120°,那么它所对的弦长为( )
2.在⊙O中, 所对的圆心角为60°,且弦AB=5cm,则 的长为( )
C
A
做一做
3、如图,在扇形OAB中,∠AOB=90°,已以AB为直径画半圆,则阴影部分面积是( )
A.大于S△AOB B.等于S △AOB
C.小于S △AOB D.不能确定与S △AOB的关系
4.如图,正方形的边长为2,以边长为直径在正方形内画半圆,则阴影部分面积是( )
A.π- 4 B. 4- π C.π- 2 D.4- π/4
B
B
5.一个形如圆锥的冰淇淋纸筒,其底面直径为6cm,母线长5cm,则它的侧面积是( )
A.66π B.30π C.28π D.15π
6.在半径为6cm的圆中,120°的圆心角所对的弧长为 .
7.扇形半径为12,面积为9π,它的圆心角等于 度
D
4πcm
22.5
8.已知扇形的面积为24π ,弧长为8πcm,则扇形的半径是 cm,圆心角是 度
6
240
9.已知扇形的面积是12 ,半径是8cm,则扇形周长是 .
10.圆锥的底面半径是1cm,母线是2cm,则高是 cm,侧面积是 ,全面积是 。
19
2π
3π
11、如图,在⊙O中,弦AC=2cm,圆周角∠ABC=45°求阴影部分面积
12、如图,把Rt△ABC的斜边放在直线 l 上,按顺时针方向在 l 上转动2次,使它转到△A2B2C2的位置.设BC=1,AC=
求(1)点A所经过的路线长.
(2)点A所经过的路线与直线l所围成的面积.
13、如图,已知扇AOB,∠AOB=90°,OA=OB=4,以OA为直径作半圆⊙M,作MP∥OB交AB于P,交⊙M于点Q,求阴影部分面积.
14、一个圆锥的侧面展开图是半径为18cm,圆心角为2400的扇形,求这个圆锥的高。
15、下图是由直径分别为4cm,6cm和10cm的三个半圆所组成的图形,求图中阴影部分的周长和面积。
16、如图,一个圆锥的高为 cm,侧面展开图是半圆,求
(1)圆锥母线l与底面半径之比.
(2)圆锥的表面积.
17、巳知圆锥的轴截面周长为10cm,设腰长为x,圆锥的表面积为S,求: ⑴ S关于X的函数表达式和自变量X的取值范围; ⑵ 画出这个函数图象,确定S的取值范围
例题解析:
1、我国某些东南沿海地区常会受到台风的侵袭,某日A市气象台测得台风中心在A市正东方向400km的B处,正快速向西北方向运动,距台风中心300km的范围内将受到影响,问A市是否会受到这次台风的影响?为什么?
A
B
D
东
北
C
2、如图,P1是一块半径为1的半圆纸板,在P1的左下角剪去一个半径为 的半圆后,得到图形P2,然后依次剪去一个更小的半圆(其直径为前一个被剪去半圆的半径)得到图形P3,P4,P5…,Pn,…,记纸板Pn的面积为Sn,试计算求出S2 ,S3 ,并猜测得到Sn-Sn-1= ,(n≥2)。
P1
P2
P3
P4
3、如图,已知⊙O的半径为5,点O到弦AB的距离为3,则⊙O上到弦AB所在直线的距离为2的点有( )个。
A、1 B、2 C、3 D、4
4、如图,⊙C经过原点且与坐标轴分别交于点A与点B,点A的坐标为(0,4),M是圆上一点,∠BMO=120°,求⊙C的半径和圆心C的坐标。
A
B
C
M
O
X
Y
D
G
5、已知P(x,y)是以坐标原点为圆心,5为半径的圆周上的点,若x,y都是整数,则这样的点共有( )个。
A、4 B、8 C、12 D、16
6、钟表的轴心到分针针端的长为5cm,若经过40min,求分针针端转过的弧长。
7、如图,有一块圆形铁皮,BC是⊙O的直径,AB=AC,在此圆形铁皮中剪下一个扇形(阴影部分)。
(1)当⊙O的半径为2时,求这个扇形(阴影部分)的面积(结果保留π)
(2)当O的半径为R0(R0>2)时,在剩下的三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由。
A
B
C
E
F
O
同课章节目录
