代数式复习

课件21张PPT。第四章 代数式
复习世间最可宝贵的就是“今”，最易丧失的也是“今”。
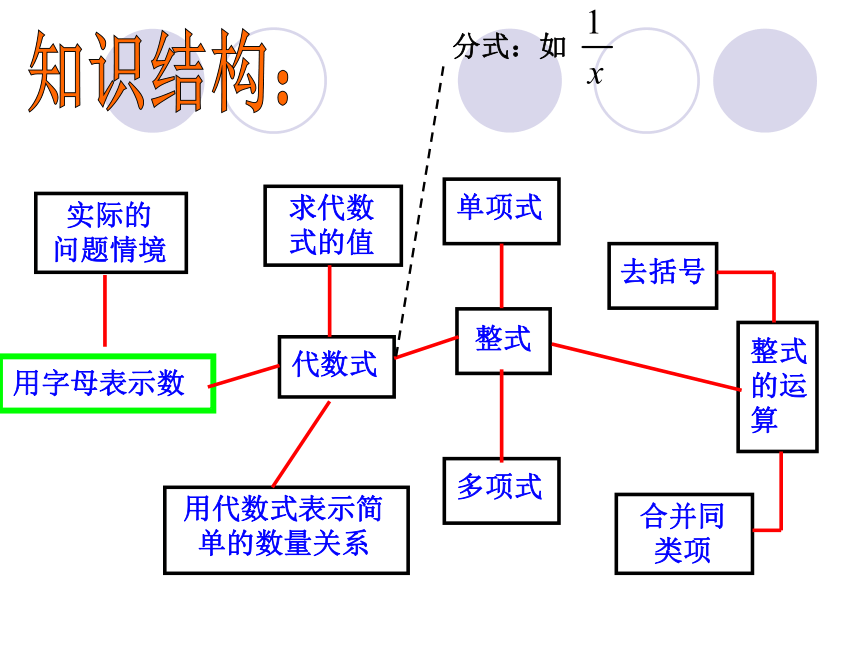
——李大钊 知识结构：分式：如1、一个代数式一般由数、表示数的字母
和运算符号组成，这里的运算是指：
、 、 、
、 、 。 单独
的一个数或者一个字母也称代数 式。知识要点：用数代替代数式里的字母，计算后所得的
结果叫做 。加法减法乘法除法乘方开方代数式的值基本内容和主要知识
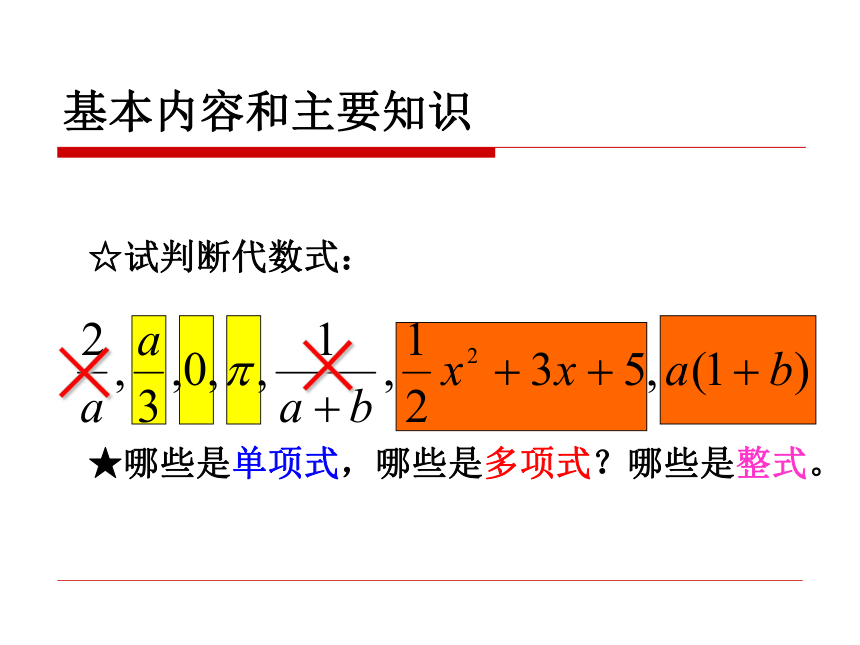
☆试判断代数式：
★哪些是单项式，哪些是多项式？哪些是整式。×× 由数与字母或字母与字母相乘组成的代
式叫做 ；
单项式中数字因数叫做这个单项式的 ；所有字母的指数的和叫做这个单项式的 。 由几个 相加组成的代数式叫做
多项式。在多项式中，每个单项式叫做多项
式的 ；不含字母的项叫做 ；
就是这个多项式的次
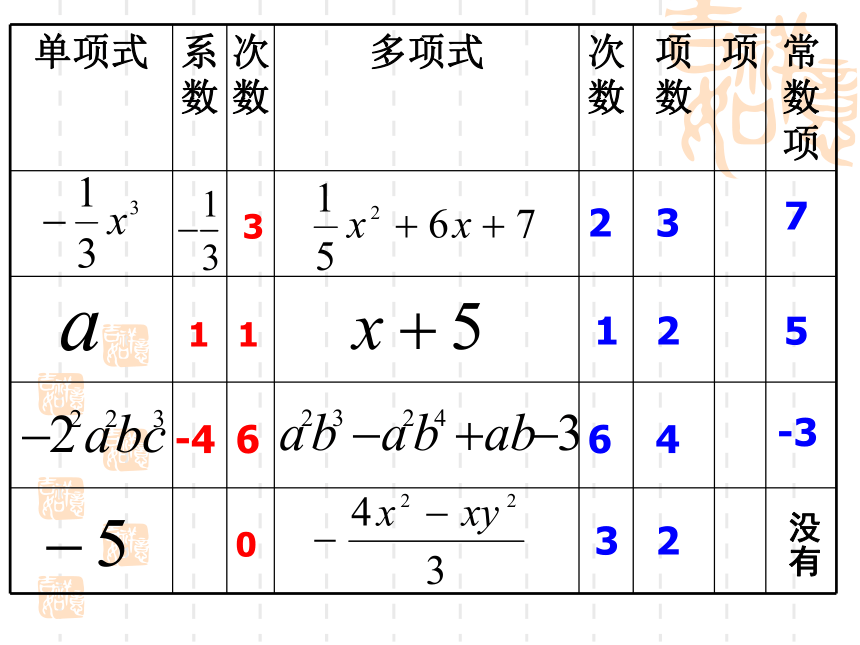
数。单项式系数次数单项式项常数项次数最高的项的次数单项式、多项式统称为 。整式★☆
311-4602312643275-3没有用代数式表示：（2）某产品的价格是 p 元，其中成本比
其价格少10%，则此产品的成本是
。（1）比 a 的5倍小 3 的数是 。（3）一本书有 m 页，第一天读了全书页数
的 四分之一，第二天读了剩下的三分
之一，则没有读的页数是 。5a - 30.9p0.5m1) x的3倍与y的差2) v1 与 v2 的和除S所得的商3) x的平方与1的和的平方根用代数式表示下列各题：4)a与b的平方和5) a与b 的和的平方6) a的相反数的倒数 3、多项式中，所含 相同，并且
也相同的项，叫做
同类项。字母相同字母的指数下列各题两项，哪些是同类项？请思考：4、主要运算法则：（1）合并同类项法则：把同类项的 相
加，所得的结果作为系数，
不变。（2）去括号法则：括号前面是 “ + ” 号，
把 去掉，括
号里各项 ；系数字母和字母的指数括号和它前面的“+”号都不变号（3）整式的加减运算可归结为 和
。（2）去括号法则：括号前面是 “ - ” 号，
把 去掉，括
号里各项 。去括号的
法则的依据是分配律，即：
a ( b + c ) = 。括号和它前面的“ – ”号都改变符号ab + ac去括号合并同类项化简这个多项式：
（1 – 3x2 + x ）- 2（5x2 + 3x – 2 ）= 1 – 3x2 + x - 10x2 - 6x + 4 = 5 – 13x2 -5x先化简再求值：已知a=-5，求代数式1-(3a+1)+a2的值。何为最简形式 已知代数式 ( 3a2 – ab+2b2 ) – ( a2 – 5ab+b2)
– 2 ( a2 + 2ab +b2 )。 （1）试说明这个代数式的值与 a 的取值
无关； （2）若 b = - 2 ，求这个代数式的值。解：( 1 ) 原式= 3a2 – ab+2b2 –a2 + 5ab -b2
– 2a2 - 4ab - 2b2= – b2 所以，代数式的值与a 的值无关。（2）当 b = - 2 时，原式 = - (-2)2 = - 4 。1、主要方法和技能：（1）用代数式表示实际生活中的量，求代数式的值；
（2）整式的加减，并解决简单实际问题。小结：2、数字与字母相乘时数字因数写在前面，并写成省略乘号的形式;
1、字母与字母相乘时应写成省略乘号的形式;3、当数字因数是带分数时应化成假分数;4、当系数是1或-1时的1应省略不写;5、表示两者相除时应把除号写成分数线;6、后接单位的若干个单项式相加， 要用括号括起来，比如（2a+3b)元。
2、书写代数式时应注意的事项:1、当 m = 时，代数式 3xmy与 –2x2 y
是同类项。2、若 a – b =10，那么15 – a + b 的值是 。3、若 A – (- 3x ) = x2 + 3x – 1 ，则 A= 。2515 – a + b = 10 – ( a – b ) = 15 – 10 = 5 A= (x2 + 3x – 1) + ( - 3x )= x2 – 1x2 – 1练习：解： 原式 = a – 2b 当 a = 6 , b = - 2 时

原式 = a – 2b = ×6 – 2 ×( - 2 )=24先化简再求值：作业：期末试卷一张