3.1直线和圆的位置关系
图片预览





文档简介
课件19张PPT。 3.1直线与圆的位置关系(3)经过半径的外端并且垂直这条半径的直线是圆的切线切线的判定定理:这个定理不仅可以用来判定圆的切线,还可以依据它来画切线.温故知新切线的判定方法有:③切线的判定定理。②直线到圆心的距离等于圆的半径。①直线与圆有唯一个公共点。温故知新经过半径的外端并且垂直这条半径的直线是圆的切线(已知切点)(未知切点) ⑴、经过半径外端的直线是圆的切线。
⑵、垂直于半径的直线是圆的切线。
⑶、过直径的外端并且垂直于这条直径的
直线是圆的切线。
⑷、和圆只有一个公共点的直线是圆的切
线。
⑸、以等腰三角形的顶点为圆心,底边上
的高为半径的圆与底边相切。
1、是非题:判断下列命题是否正确。(×)(×)(√)(√)(√)
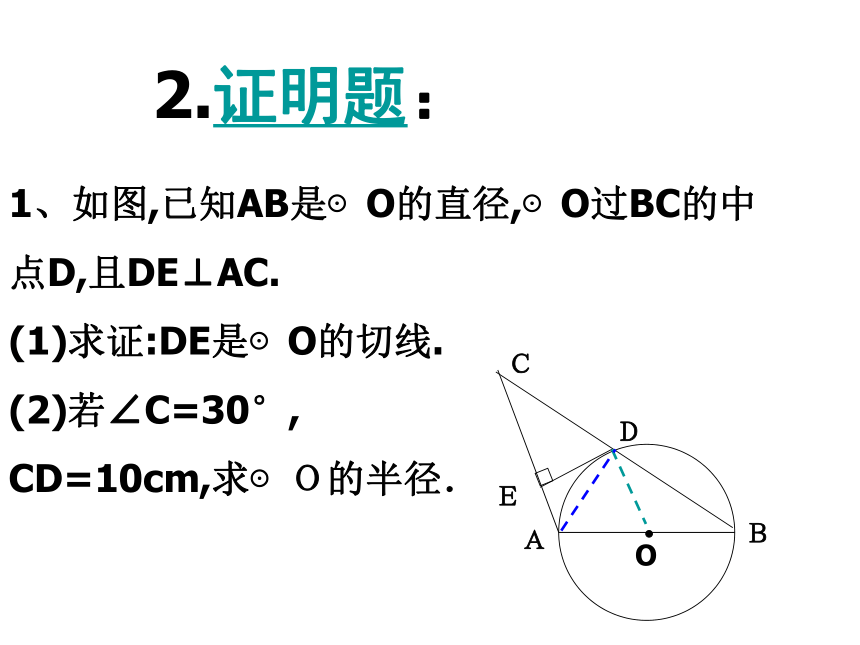
1、如图,已知AB是⊙O的直径,⊙O过BC的中
点D,且DE⊥AC.
(1)求证:DE是⊙O的切线.
(2)若∠C=30°,
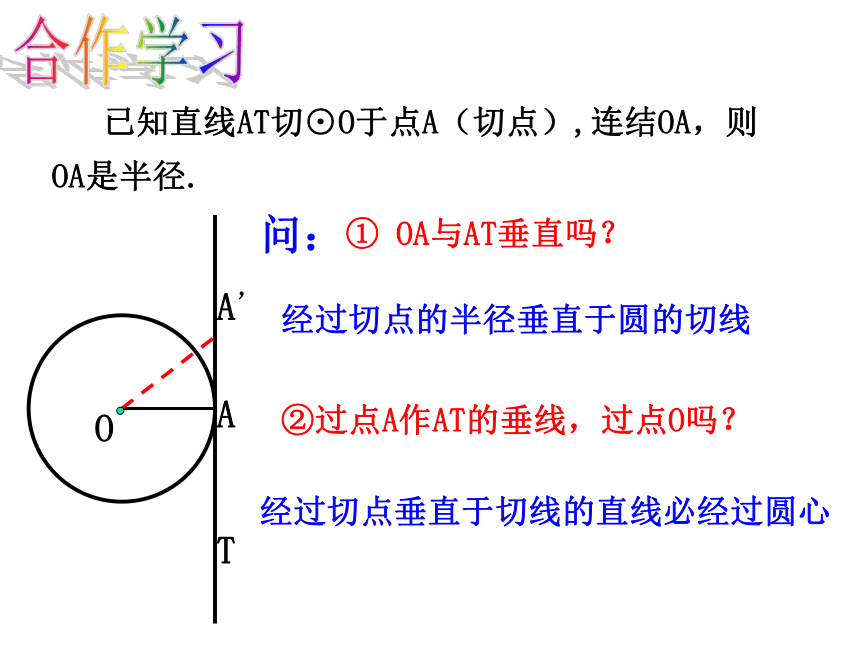
CD=10cm,求⊙O的半径.OABCDE2.证明题:AOTA’ ① OA与AT垂直吗?②过点A作AT的垂线,过点O吗?问: 已知直线AT切⊙O于点A(切点),连结OA,则OA是半径.经过切点的半径垂直于圆的切线经过切点垂直于切线的直线必经过圆心合作学习知识要点一般地,圆的切线有如下的性质:经过切点的半径垂直于圆的切线经过切点垂直于切线的直线必经过圆心∵⊙O与AT相切于点A
∴OA⊥AT∵ ⊙O与AT相切于点A,PA⊥AT,交圆于P点
∴AP是圆的直径几何语言补充:经过圆心垂直于切线的直线必经过切点∵ ⊙O与AT相切,OA⊥AT,
∴A是切点课堂练习1、已知直线l是⊙O的切线,P为切点。 (1)经过圆心O作l的垂线,垂足是__________
(2)经过点P作垂直于l的弦,这条弦是⊙ O的___________
(3)连结OP,则OP与直线l的位置关系是_________;切点P直径垂直2、求证:若圆的两条切线互相平行,则连结两切点的线段是直径;已知:l1,l2是⊙O的两条切线,且l1∥l2,A,B是切点,连结AB
求证:AB是⊙ O的直径;归纳小结切线的性质定理: 1、经过圆心垂直于切线的直线必经过切点; 2、圆的切线垂直于经过切点的半径; 3、经过切点垂直于切线的直线必经过圆心。垂直于切线过切点过圆心例1如图,AB是⊙O的直径,BC是和⊙ O相切于点B的切线, ⊙ O的弦AD平行于OC,
求证:DC是⊙ O的切线COBDA例2、木工师傅可以用角尺测量并计算出圆的半径.如图,用角尺的较短边紧靠⊙O于点A,并使较长边与⊙O相切于点C,记角尺的直角顶点为B,量得AB=8cm,BC=16cm.求⊙O的半径.OABCD解:连结OA,OC,过点A作AD⊥OC于D.∵⊙O与BC相切于点C.
∴OC⊥BC∵AB⊥BC,AD⊥OC
∴四边形ABCD是矩形
∴AD=BC,OD=OC-CD=OC-AB在Rt△ADO中,即解得:r=20
答: ⊙O的半径为20cm连结过切点的半径是常用的辅助线例3.如图,直线AB与⊙O相切于点C,AO与⊙O交于点D,连结CD.求证:CBAODE 证明:作OE⊥DC于点E,∵△ODC是等腰三角形∵⊙O与AB相切于点C
∴OC⊥AB∴∠ACD=∠COE=900-∠OCE数学知识:切线与弦所夹的角叫弦切角,它的度数等于所夹弧的度数,等于所夹弧所对圆心角度数的一半,等于所夹弧所对的圆周角的度数.(2009年佳木斯)如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于E,连接AD,则下列结论正确的个数是( )
①AD⊥BC ②∠EDA=∠B ③OA=AC ④DE是⊙O的切线
A.1 个 B.2个 C.3 个 D.4个链接中考2、如图,AT切⊙O于点A,AB⊥AT,交⊙O于点B,BT交⊙O于点C。已知∠B=300,AT= 。求⊙O的直径和弦BC的长。1、如图,直线l切⊙O于点P,弦AB∥l,请说明
的理由 圆的切线垂直于经过切点的半径 经过切点垂直于切线的直线必经过圆心练一练2、如图, ⊙O切PB于点B,PB=4,PA=2,求⊙O的半径。练一练3. (2009山西省太原市)如图AB、AC是⊙O的两条弦,∠A=30°,过点C的切线与OB的延长线交于点D,则∠D的度数为 .30°3.(2009年山西省)如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,BC∥OD,AB=2,OD=3,则BC的长为( )
A. B. C. D.A课堂小结1.切线的性质:经过切点的半径垂直于圆的切线经过切点垂直于切线的直线必经过圆心2.切线性质的应用:常用的辅助线是连接半径.综合性较强,要联系许多其它图形的性质.再见!
⑵、垂直于半径的直线是圆的切线。
⑶、过直径的外端并且垂直于这条直径的
直线是圆的切线。
⑷、和圆只有一个公共点的直线是圆的切
线。
⑸、以等腰三角形的顶点为圆心,底边上
的高为半径的圆与底边相切。
1、是非题:判断下列命题是否正确。(×)(×)(√)(√)(√)
1、如图,已知AB是⊙O的直径,⊙O过BC的中
点D,且DE⊥AC.
(1)求证:DE是⊙O的切线.
(2)若∠C=30°,
CD=10cm,求⊙O的半径.OABCDE2.证明题:AOTA’ ① OA与AT垂直吗?②过点A作AT的垂线,过点O吗?问: 已知直线AT切⊙O于点A(切点),连结OA,则OA是半径.经过切点的半径垂直于圆的切线经过切点垂直于切线的直线必经过圆心合作学习知识要点一般地,圆的切线有如下的性质:经过切点的半径垂直于圆的切线经过切点垂直于切线的直线必经过圆心∵⊙O与AT相切于点A
∴OA⊥AT∵ ⊙O与AT相切于点A,PA⊥AT,交圆于P点
∴AP是圆的直径几何语言补充:经过圆心垂直于切线的直线必经过切点∵ ⊙O与AT相切,OA⊥AT,
∴A是切点课堂练习1、已知直线l是⊙O的切线,P为切点。 (1)经过圆心O作l的垂线,垂足是__________
(2)经过点P作垂直于l的弦,这条弦是⊙ O的___________
(3)连结OP,则OP与直线l的位置关系是_________;切点P直径垂直2、求证:若圆的两条切线互相平行,则连结两切点的线段是直径;已知:l1,l2是⊙O的两条切线,且l1∥l2,A,B是切点,连结AB
求证:AB是⊙ O的直径;归纳小结切线的性质定理: 1、经过圆心垂直于切线的直线必经过切点; 2、圆的切线垂直于经过切点的半径; 3、经过切点垂直于切线的直线必经过圆心。垂直于切线过切点过圆心例1如图,AB是⊙O的直径,BC是和⊙ O相切于点B的切线, ⊙ O的弦AD平行于OC,
求证:DC是⊙ O的切线COBDA例2、木工师傅可以用角尺测量并计算出圆的半径.如图,用角尺的较短边紧靠⊙O于点A,并使较长边与⊙O相切于点C,记角尺的直角顶点为B,量得AB=8cm,BC=16cm.求⊙O的半径.OABCD解:连结OA,OC,过点A作AD⊥OC于D.∵⊙O与BC相切于点C.
∴OC⊥BC∵AB⊥BC,AD⊥OC
∴四边形ABCD是矩形
∴AD=BC,OD=OC-CD=OC-AB在Rt△ADO中,即解得:r=20
答: ⊙O的半径为20cm连结过切点的半径是常用的辅助线例3.如图,直线AB与⊙O相切于点C,AO与⊙O交于点D,连结CD.求证:CBAODE 证明:作OE⊥DC于点E,∵△ODC是等腰三角形∵⊙O与AB相切于点C
∴OC⊥AB∴∠ACD=∠COE=900-∠OCE数学知识:切线与弦所夹的角叫弦切角,它的度数等于所夹弧的度数,等于所夹弧所对圆心角度数的一半,等于所夹弧所对的圆周角的度数.(2009年佳木斯)如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于E,连接AD,则下列结论正确的个数是( )
①AD⊥BC ②∠EDA=∠B ③OA=AC ④DE是⊙O的切线
A.1 个 B.2个 C.3 个 D.4个链接中考2、如图,AT切⊙O于点A,AB⊥AT,交⊙O于点B,BT交⊙O于点C。已知∠B=300,AT= 。求⊙O的直径和弦BC的长。1、如图,直线l切⊙O于点P,弦AB∥l,请说明
的理由 圆的切线垂直于经过切点的半径 经过切点垂直于切线的直线必经过圆心练一练2、如图, ⊙O切PB于点B,PB=4,PA=2,求⊙O的半径。练一练3. (2009山西省太原市)如图AB、AC是⊙O的两条弦,∠A=30°,过点C的切线与OB的延长线交于点D,则∠D的度数为 .30°3.(2009年山西省)如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,BC∥OD,AB=2,OD=3,则BC的长为( )
A. B. C. D.A课堂小结1.切线的性质:经过切点的半径垂直于圆的切线经过切点垂直于切线的直线必经过圆心2.切线性质的应用:常用的辅助线是连接半径.综合性较强,要联系许多其它图形的性质.再见!
