4.2 相似三角形
图片预览




文档简介
课件15张PPT。黄山松中国地图 我们刚才所见到的图形有什么 相同和不同的地方?相同点: 形状相同.
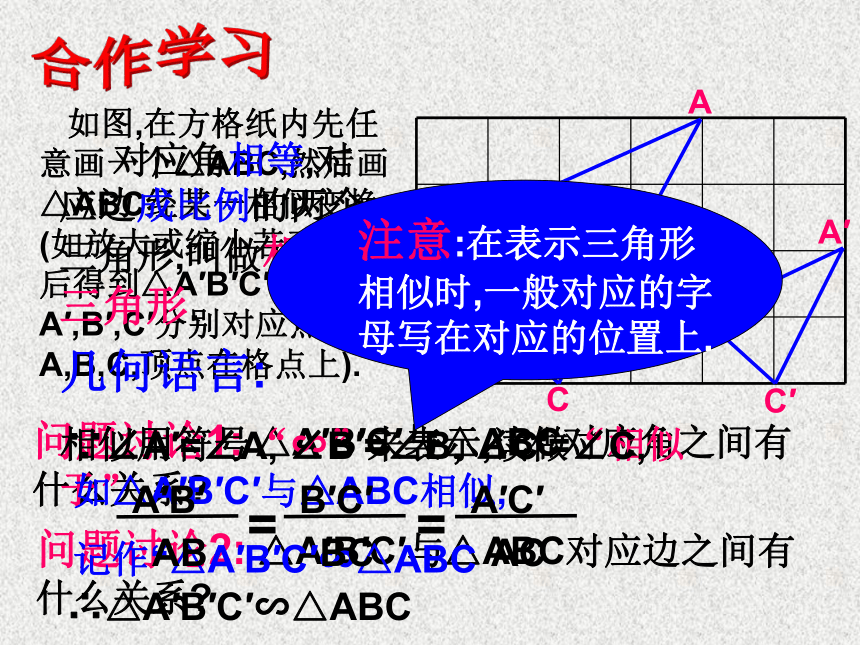
不同点: 大小不同. 生活中我们会碰到许多这样形状相同的.大小不一定相同的图形,在数学上,我们把具有相同形状的图形称为:相似图形知识回顾相似变换的性质: 图形的相似变换不改变图形中每一个角的大小;图形中的每条线段都扩大(或缩小)相同的倍数.4.2相似三角形 如图,在方格纸内先任意画一个△ABC,然后画△ABC经某一相似变换(如放大或缩小若干倍)后得到△A′B′C′(点A′,B′,C′分别对应点A,B,C,顶点在格点上).问题讨论1: △A′B′C′与△ABC对应角之间有什么关系?问题讨论2: △A′B′C′与△ABC对应边之间有什么关系?合作学习 对应角相等,对应边成比例的两个三角形,叫做相似三角形.相似用符号“∽”来表示,读做“相似于”如△A′B′C′与△ABC相似,
记作“△A′B′C′∽△ABC几何语言:∴△A′B′C′∽△ABC试一试 根据相似三角形的定义,你能归纳出相似三角形的性质吗?BAC相似三角形的对应角相等,对应边成比例.如图,∵ △A′B′C′∽△ABC∴ ∠A′=∠A, ∠B′=∠B, ∠C′=∠C, 相似三角形对应边的比,叫做两个相似三角形的相似比(或相似系数)△ABC与△A′B′C′的相似比为 .2例1 已知:如图,D,E分别是AB,AC边的中点.
求证:△ADE∽△ABC.证明:∵D,E分别是AB,AC的中点,∴∠ADE=∠B,∠AED=∠C在△ADE和△ABC中,∠ADE=∠B,∠AED=∠C,∠A=∠A∴DE∥BC,DE= BC.∴△ADE∽△ABC (相似三角形的定义)相似三角形的定义可以作为三角形相似的一种判定方法.(1)两个直角三角形一定相似吗?(2)两个等腰三角形一定相似吗?(3)有没有哪类特殊三角形一定相似呢?我想,我说? 例2 如图,D、E分别是△ABC的AB,AC边上的点, △ABC∽ △ADE.
已知AD:DB=1:2,BC=9cm,求DE的长
变式:如图,D,E分别是△ABC的边AB,AC上的点,
点D与点B是对应点. △ ADE ∽△ ABC.
已知AD﹕DB=1﹕2,BC=9cm,求DE的长.体会.分享 请你谈谈对相似三角形的认识,让大家与你分享吧!1、相似三角形定义:对应角相等, 对应边成比例的两个三角形 △ABC∽△DEF3、相似三角形的性质:对应角相等,对应边
对应成比例。2、相似三角形的判定:利用三角形相似的定义∠A = ∠D,∠B = ∠E,
∠C = ∠FABC∽ △DEF定义性质1.如图,D是AB上的一点。 △ABC∽ △ACD ,且AD:AC=2:3,∠ADC= 65°, ∠B=43 °.
(1)求∠ABC, ∠ACD的度数;
(2)写出△ABC与 △ACD的对应边成比例的比例式,求出相似比。 2、如图,AB,CD相交于点0, △AOC∽ △BOD 。
(1)如果OC:OD=1:2,AC=5,求BD的长;
(2)如果∠A=35°, ∠AOC=100°,求∠D的度数。益智的“模型”这是两个极具代表性的相似三角形基本模型: “A”型和“X” 型若△ADE∽ △ABC,则
∠DAE=∠BAC, ∠ADE=∠ A BC,
∠AED=∠ACB,若△ABC∽ △DEC,则
∠A=∠D, ∠B=∠E,
∠ACB=∠DCE,
不同点: 大小不同. 生活中我们会碰到许多这样形状相同的.大小不一定相同的图形,在数学上,我们把具有相同形状的图形称为:相似图形知识回顾相似变换的性质: 图形的相似变换不改变图形中每一个角的大小;图形中的每条线段都扩大(或缩小)相同的倍数.4.2相似三角形 如图,在方格纸内先任意画一个△ABC,然后画△ABC经某一相似变换(如放大或缩小若干倍)后得到△A′B′C′(点A′,B′,C′分别对应点A,B,C,顶点在格点上).问题讨论1: △A′B′C′与△ABC对应角之间有什么关系?问题讨论2: △A′B′C′与△ABC对应边之间有什么关系?合作学习 对应角相等,对应边成比例的两个三角形,叫做相似三角形.相似用符号“∽”来表示,读做“相似于”如△A′B′C′与△ABC相似,
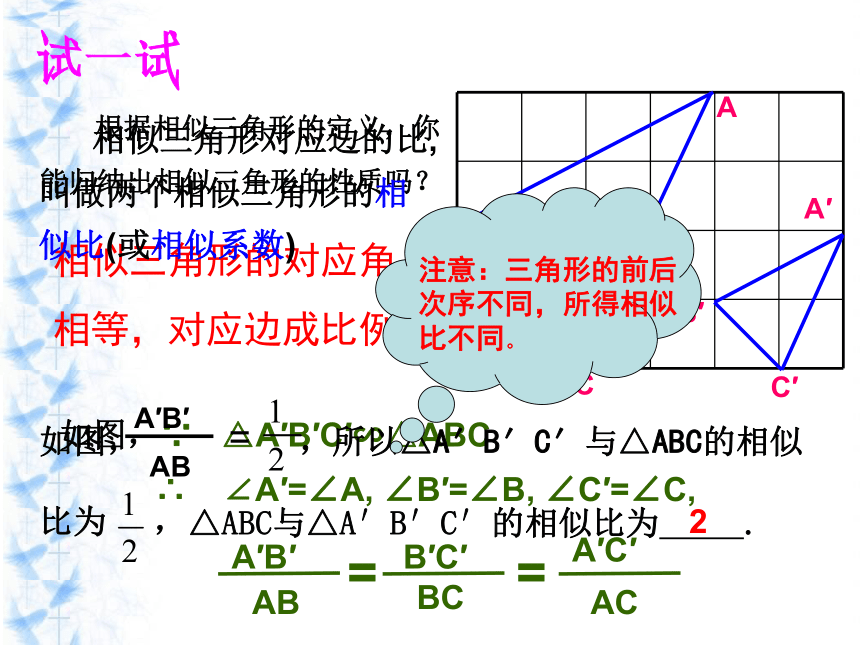
记作“△A′B′C′∽△ABC几何语言:∴△A′B′C′∽△ABC试一试 根据相似三角形的定义,你能归纳出相似三角形的性质吗?BAC相似三角形的对应角相等,对应边成比例.如图,∵ △A′B′C′∽△ABC∴ ∠A′=∠A, ∠B′=∠B, ∠C′=∠C, 相似三角形对应边的比,叫做两个相似三角形的相似比(或相似系数)△ABC与△A′B′C′的相似比为 .2例1 已知:如图,D,E分别是AB,AC边的中点.
求证:△ADE∽△ABC.证明:∵D,E分别是AB,AC的中点,∴∠ADE=∠B,∠AED=∠C在△ADE和△ABC中,∠ADE=∠B,∠AED=∠C,∠A=∠A∴DE∥BC,DE= BC.∴△ADE∽△ABC (相似三角形的定义)相似三角形的定义可以作为三角形相似的一种判定方法.(1)两个直角三角形一定相似吗?(2)两个等腰三角形一定相似吗?(3)有没有哪类特殊三角形一定相似呢?我想,我说? 例2 如图,D、E分别是△ABC的AB,AC边上的点, △ABC∽ △ADE.
已知AD:DB=1:2,BC=9cm,求DE的长
变式:如图,D,E分别是△ABC的边AB,AC上的点,
点D与点B是对应点. △ ADE ∽△ ABC.
已知AD﹕DB=1﹕2,BC=9cm,求DE的长.体会.分享 请你谈谈对相似三角形的认识,让大家与你分享吧!1、相似三角形定义:对应角相等, 对应边成比例的两个三角形 △ABC∽△DEF3、相似三角形的性质:对应角相等,对应边
对应成比例。2、相似三角形的判定:利用三角形相似的定义∠A = ∠D,∠B = ∠E,
∠C = ∠FABC∽ △DEF定义性质1.如图,D是AB上的一点。 △ABC∽ △ACD ,且AD:AC=2:3,∠ADC= 65°, ∠B=43 °.
(1)求∠ABC, ∠ACD的度数;
(2)写出△ABC与 △ACD的对应边成比例的比例式,求出相似比。 2、如图,AB,CD相交于点0, △AOC∽ △BOD 。
(1)如果OC:OD=1:2,AC=5,求BD的长;
(2)如果∠A=35°, ∠AOC=100°,求∠D的度数。益智的“模型”这是两个极具代表性的相似三角形基本模型: “A”型和“X” 型若△ADE∽ △ABC,则
∠DAE=∠BAC, ∠ADE=∠ A BC,
∠AED=∠ACB,若△ABC∽ △DEC,则
∠A=∠D, ∠B=∠E,
∠ACB=∠DCE,
同课章节目录
