相似三角形的性质及应用课件(1)

课件15张PPT。4。4相似三角形的性质及其应用（1） 在10倍的放大镜下看到的三角形与原三角形相比,
三角形的边长,周长,面积,角,它们有什么变化？问题2、ΔA′B′C′与ΔABC的
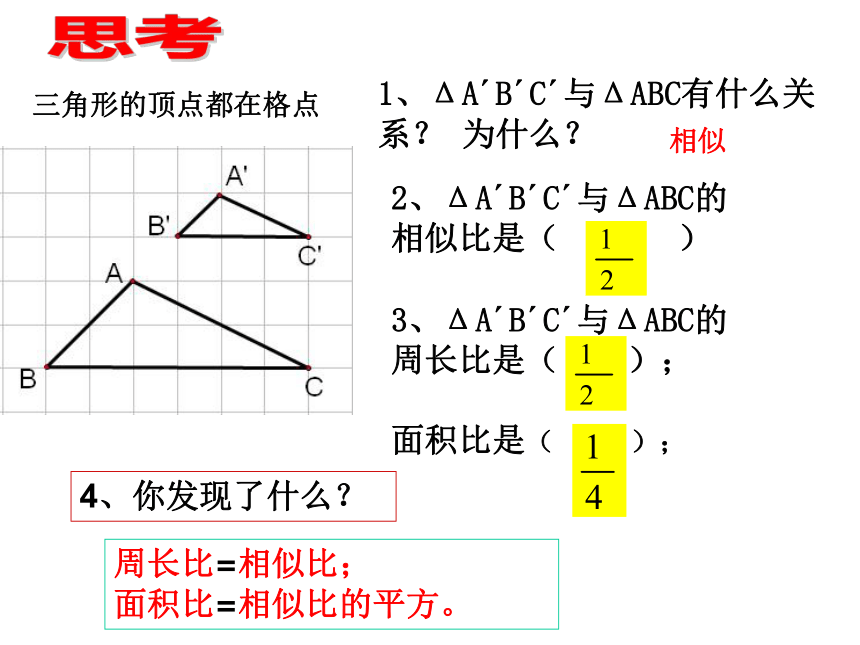
相似比是（ ）三角形的顶点都在格点
1、ΔA′B′C′与ΔABC有什么关系？ 为什么？
4、你发现了什么？思考3、ΔA′B′C′与ΔABC的
周长比是（ ）；
面积比是（ ）；相似周长比=相似比；
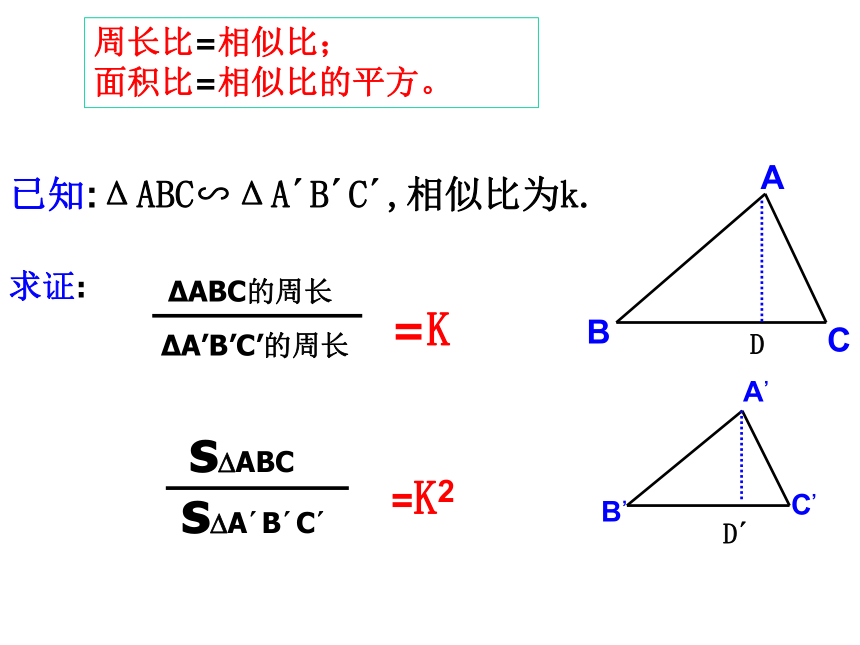
面积比=相似比的平方。已知:ΔABC∽ΔA′B′C′,相似比为k.周长比=相似比；
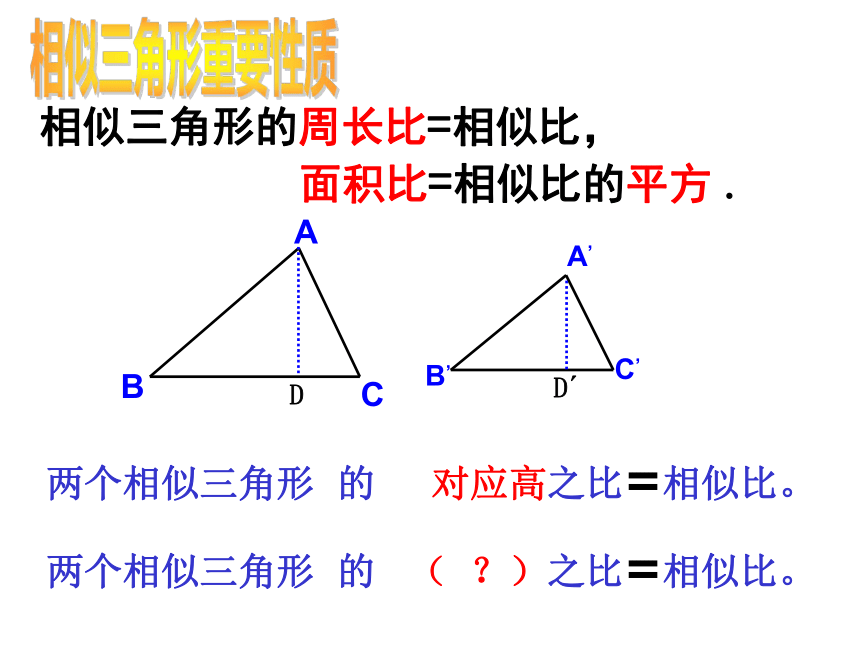
面积比=相似比的平方。相似三角形的周长比=相似比，
面积比=相似比的平方 .相似三角形重要性质两个相似三角形 的 对应高之比=相似比。两个相似三角形 的 （ ？）之比=相似比。 在10倍的放大镜下看到的三角形与原三角形相比, 三角形的边长,周长,面积,角,它们有什么变化？1、放大镜下的变化
三角形的边长放大为原来的 倍三角形的周长放大为原来的 倍.
三角形的面积放大为原来的 倍.三角形的角大小 （放大了或 没变） .
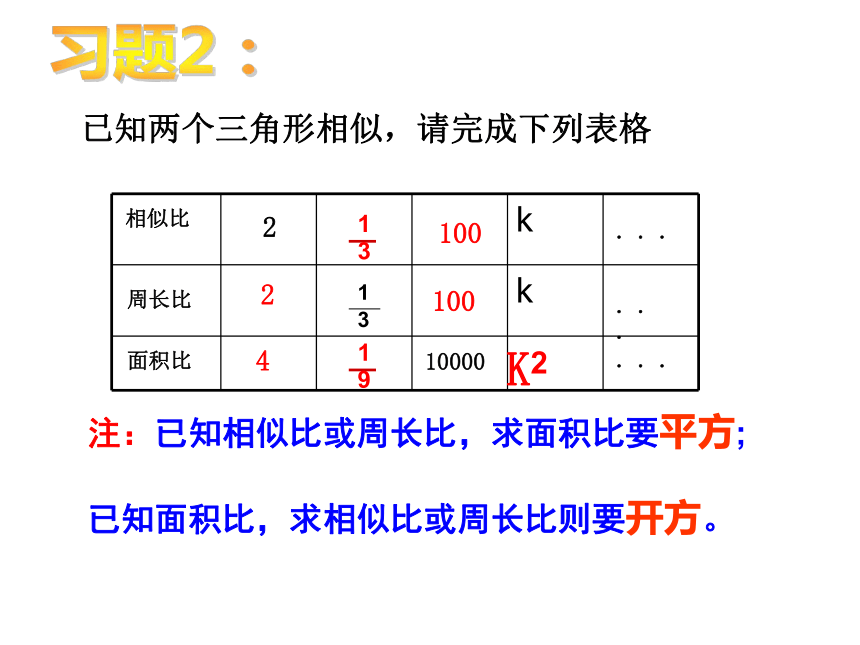
放大10倍2、放大镜下看到的三角形与原三角形存在什么关系？习题1：相似比=？10：1请解释：这些数据怎么来的？已知两个三角形相似，请完成下列表格相似比周长比面积比注：已知相似比或周长比，求面积比要平方;

已知面积比，求相似比或周长比则要开方。习题2：24100100100002．．．．．．．．．K2习题3、分别将三角形做如下相似变换，并完成填空：
（1）如果三角形的边长扩大为原来的100倍，那么三角形的周长扩大为原来的 倍；面积扩大为原来的 倍；
（2）如果将三角形的面积扩大为原来的100倍，那么三角形的边长扩大为原来的 倍；
（3）如果三角形的周长扩大为原来的100倍，那么三角形的边长扩大为原来的 倍；习题4、如图，D，E分别是AC，AB边上的点，∠ADE=∠B，AG⊥BC于点G，AF⊥DE于点F，若AD=3，AB=5。求：
（1） ;
（2）△ADE与△ABC的周长比;（3）△ADE与△ABC的面积比。 例题.如图是某市部分街道图，比例尺是1:10000，请你估计三条道路围成的三角形地块ABC的实际周长和面积.1、地图上的△ABC与实际三角形地块有什么关系？3、利用什么等量关系 求 △ ABC地块的实际周长和面积?2、相似比是（ ）习题5、如图，在等边△ ABC中，点D，E分别在AB、AC边上，且DE//BC。如果BC=8厘米，AD：DB=1：3。
（1）求△ ADE的周长
（2）求△ ADE的面积探究活动已知△ABC，如果要作与BC平行的直线把△ABC划分成两部分，使这两部分（三角形与四边形）的面积之比为1:1，该怎么作？
如果要使划分成的面积之比为1:2，又该怎么作？
如果要使划分成的面积之比为1:n,又该怎么作？习题6： 如图，在△ABC中，点D，E，F分别在边AB、AC，BC上，且DE//BC，EF//BC。已知AD：DB=2：3，S△ABC= 100.
求:ΔADE的面积等于多少？
四边形BDEF面积为多少？习题7：相似三角形的周长比=相似比，
面积比=相似比的平方 .两个相似三角形 的 对应高之比=相似比。小结1、在应用这些性质时,该注意些什么？
2、学了这些性质，你体会到了什么数学思想？
化归与转化思想、方程思想 若设SΔABC=S, SΔADE=S1, SΔEFC=S2.
请猜想：S与S1、S2之间存在怎样数量的关系？
你能加以验证吗？S1习题8：S2