相似三角形的性质及其应用(2
图片预览


文档简介
课件15张PPT。 §4.4 相似三角形的性质及其应用(2)1、相似三角形对应角相等。
2、 对应边成比例。
3、 周长之比=相似比;
4、 面积之比=相似比的平方。
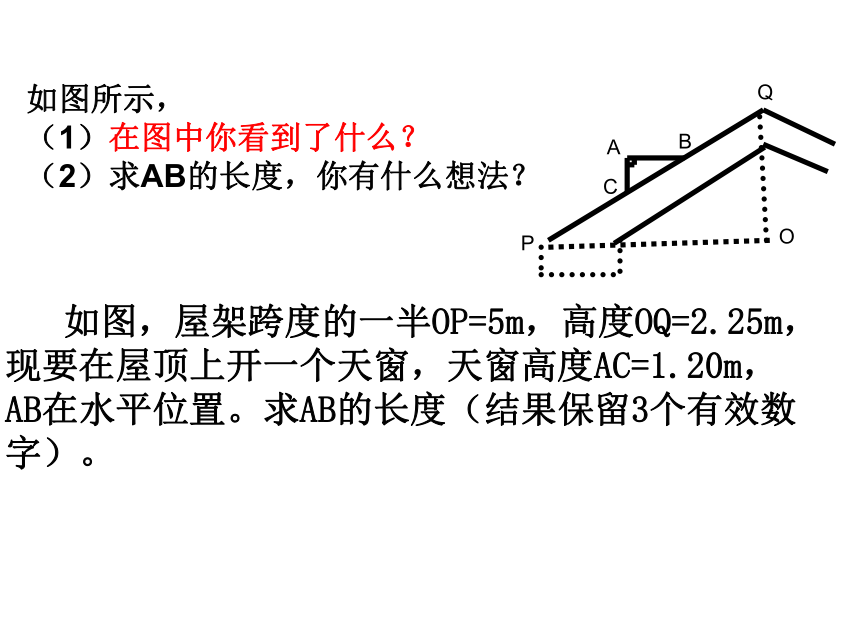
5、 对应边上的高线之比=相似比. 如图,屋架跨度的一半OP=5m,高度OQ=2.25m,现要在屋顶上开一个天窗,天窗高度AC=1.20m,AB在水平位置。求AB的长度(结果保留3个有效数字)。如图所示,
(1)在图中你看到了什么?
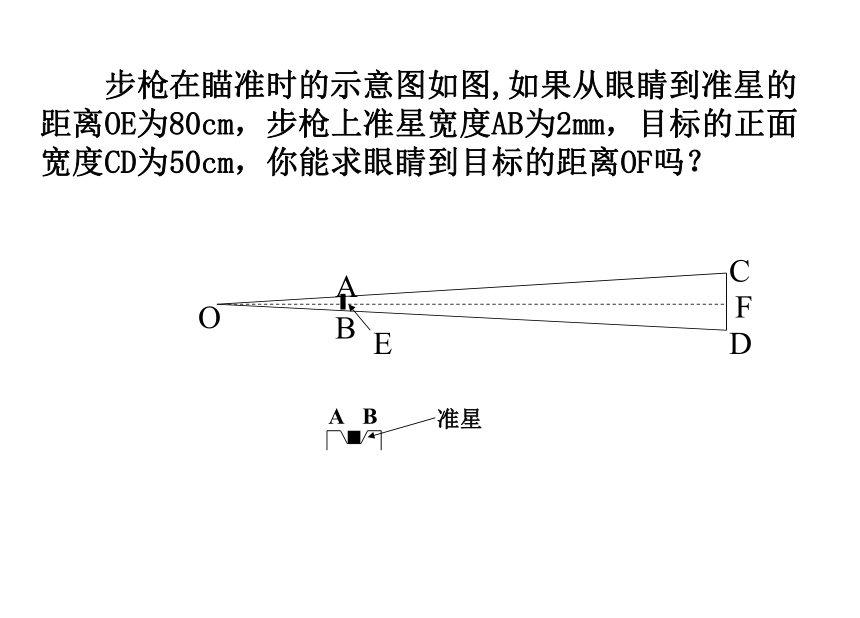
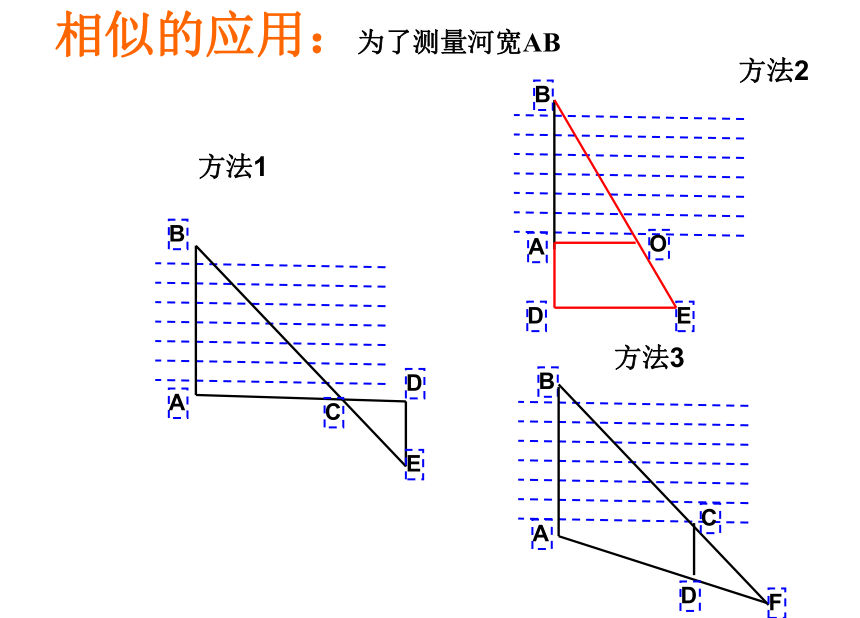
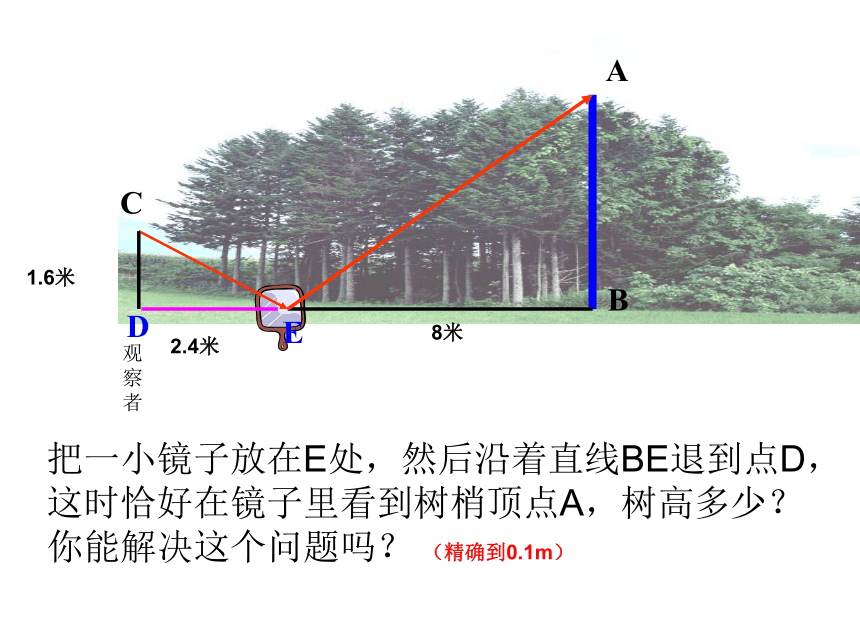
(2)求AB的长度,你有什么想法? 步枪在瞄准时的示意图如图,如果从眼睛到准星的距离OE为80cm,步枪上准星宽度AB为2mm,目标的正面宽度CD为50cm,你能求眼睛到目标的距离OF吗? A B相似的应用:为了测量河宽ABAB方法3方法1FAB方法2要测量树的高度,你有什么方法? 把一小镜子放在E处,然后沿着直线BE退到点D,这时恰好在镜子里看到树梢顶点A,树高多少?
你能解决这个问题吗? (精确到0.1m)ABE8米2.4米 把长为2.40m的标杆CD直立在地面上,量出树的影长为2.80m,标杆的影长为1.47m。这时树高多少?你能解决这个问题吗? (精确到0.1m)ABAA2.42.81.47平面镜法标杆法1.某一时刻树的影长为8米,同一时刻身高为1.5米的人的影长为3米,则树高为 . 2.铁道的栏杆的短臂为OA=1米,长臂OB=10米,短臂端下降AC=0.6米,则长臂端上升BD = 米。4米6体验3.如图:小明在打网球时,要使球恰好能打过网 ,而且落在离网5米的位置上,则拍击球的高度应为( ) 。A、2.7米 B、1.8米 C、0.9米 D、 6米 A 1、如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?NMQPEDCBA解:设正方形PQMN是符合要求的正方形,△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
因为PN∥BC,所以△APN∽ △ABC
所以挑战自我问题一
◆树高、河宽的这两个实际问题(不可能直接使用皮尺去量)
常用什么方法解这类“求树高、河宽”的实际问题?(构建图形)构造相似三角形解决问题 建模思想。
首先要把实际问题转化为几何模型即建模,
再利用三角形相似的相关知识来解决。问题二:你从求树高、河宽的这两个实际问题中,体会到什么数学思想?课堂小结
2、 对应边成比例。
3、 周长之比=相似比;
4、 面积之比=相似比的平方。
5、 对应边上的高线之比=相似比. 如图,屋架跨度的一半OP=5m,高度OQ=2.25m,现要在屋顶上开一个天窗,天窗高度AC=1.20m,AB在水平位置。求AB的长度(结果保留3个有效数字)。如图所示,
(1)在图中你看到了什么?
(2)求AB的长度,你有什么想法? 步枪在瞄准时的示意图如图,如果从眼睛到准星的距离OE为80cm,步枪上准星宽度AB为2mm,目标的正面宽度CD为50cm,你能求眼睛到目标的距离OF吗? A B相似的应用:为了测量河宽ABAB方法3方法1FAB方法2要测量树的高度,你有什么方法? 把一小镜子放在E处,然后沿着直线BE退到点D,这时恰好在镜子里看到树梢顶点A,树高多少?
你能解决这个问题吗? (精确到0.1m)ABE8米2.4米 把长为2.40m的标杆CD直立在地面上,量出树的影长为2.80m,标杆的影长为1.47m。这时树高多少?你能解决这个问题吗? (精确到0.1m)ABAA2.42.81.47平面镜法标杆法1.某一时刻树的影长为8米,同一时刻身高为1.5米的人的影长为3米,则树高为 . 2.铁道的栏杆的短臂为OA=1米,长臂OB=10米,短臂端下降AC=0.6米,则长臂端上升BD = 米。4米6体验3.如图:小明在打网球时,要使球恰好能打过网 ,而且落在离网5米的位置上,则拍击球的高度应为( ) 。A、2.7米 B、1.8米 C、0.9米 D、 6米 A 1、如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?NMQPEDCBA解:设正方形PQMN是符合要求的正方形,△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
因为PN∥BC,所以△APN∽ △ABC
所以挑战自我问题一
◆树高、河宽的这两个实际问题(不可能直接使用皮尺去量)
常用什么方法解这类“求树高、河宽”的实际问题?(构建图形)构造相似三角形解决问题 建模思想。
首先要把实际问题转化为几何模型即建模,
再利用三角形相似的相关知识来解决。问题二:你从求树高、河宽的这两个实际问题中,体会到什么数学思想?课堂小结
同课章节目录
