1.3 解直角三角形(1)
图片预览






文档简介
课件24张PPT。1.3解直角三角形(1)三角函数定义回顾互余两角之间的三角函数关系:
sinA=cosB,tanA.tanB=1.特殊角300,450,600角的三角函数值.锐角三角函数同角之间的三角函数关系:
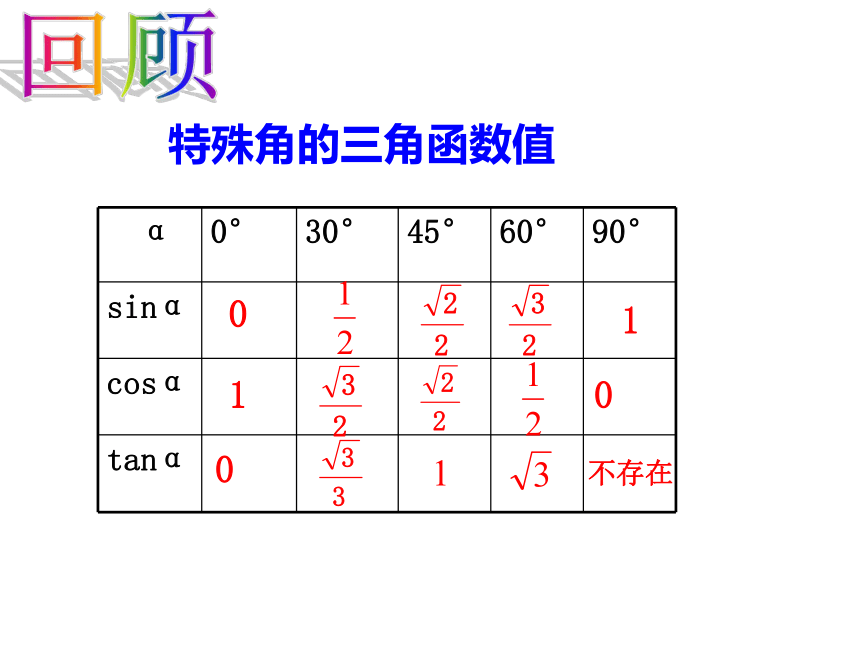
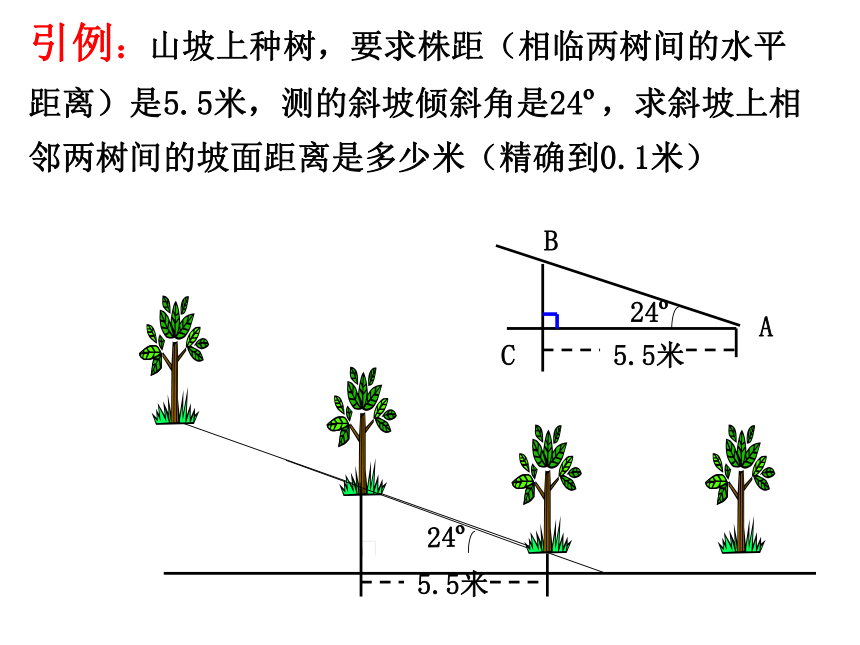
sin2A+cos2A=1.tanA=温故知新01100不存在特殊角的三角函数值回顾互余两角三角函数关系:sin(900-A)=cosAtanAtanB=1cos(900-A)=sinA回顾同角三角函数关系:sin2A+cos2A=1A+B=900引例:山坡上种树,要求株距(相临两树间的水平
距离)是5.5米,测的斜坡倾斜角是24o,求斜坡上相
邻两树间的坡面距离是多少米(精确到0.1米) 解:在Rt△ABC中,∠C=90°引例:山坡上种树,要求株距(相临两树间的水平
距离)是5.5米,测的斜坡倾斜角是24o,求斜坡上相
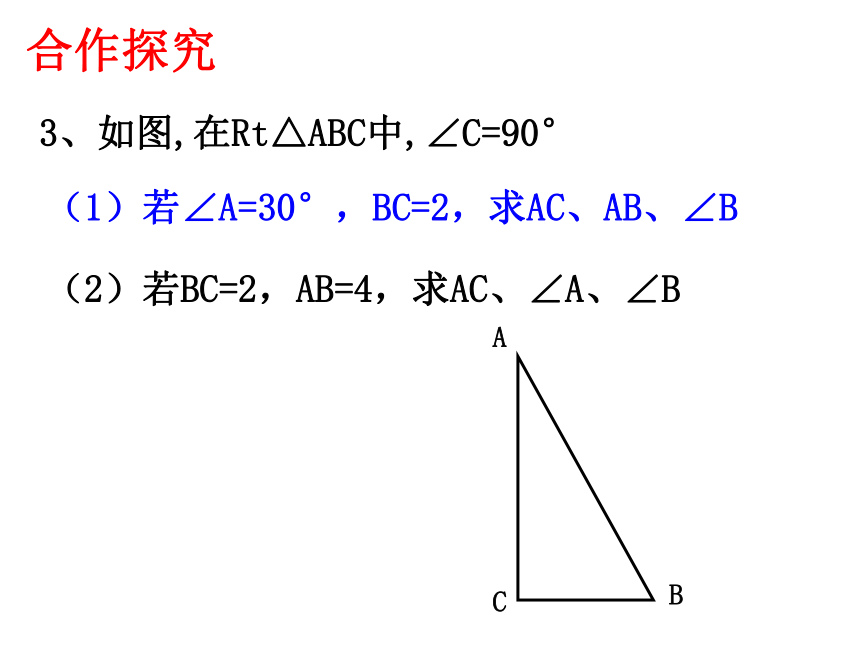
邻两树间的坡面距离是多少米(精确到0.1米)≈6.0(米)答:斜坡上相邻两树间的坡面距离是6.0米。合作探究1、已知在Rt△ABC中,∠C= Rt∠,AB=5,AC=3,求边BC的长。你能求出∠A的度数么?2、已知在Rt△ABC中, ∠C= Rt∠ ,∠A=560,AB=8,求AC的长。3、如图,在Rt△ABC中,∠C=90°(1)若∠A=30°,BC=2,求AC、AB、∠B(2)若BC=2,AB=4,求AC、∠A、∠B合作探究已知屋面的宽度L和坡顶的设计高度h(如图)。你能求出斜面钢条的长度a和倾角a 吗?想一想变化:已知平顶屋面的宽度L和坡顶的设计倾角α(如图)。你能求出斜面钢条a的长度和设计高度h吗?a 在上述例题中,我们都是利用直角三角形中的已知边、角来求出另外一些的边角.像这样,
******************************** 在直角三角形中,由已知的一些边、角,求出另一些边、角的过程,叫做解直角三角形.解直角三角形1.两锐角之间的关系:2.三边之间的关系:3.边角之间的关系A+B=900a2+b2=c2例1、如图,在Rt△ABC中,∠C=900,∠A=500,AB=3,求∠B和a,b(边长保留2个有效数字)解:Rt△ABC中∠B=900-∠A=400∴a=AB×sinA=3×sin500≈2.3∴b=AB×cosA=3×cos500≈1.9例2、如图是某市“平改坡”工程中一种坡屋顶设计,已知平顶屋面的宽度L为10m,坡屋顶的设计高度h为3.5m,能求斜面钢条a的长度和坡角a。(长度精确到0.1米,角度精确到1°)解:在Rt△ABD中,∴α≈350.答:斜面钢条a的长度约为6.1米,坡角约为350.例2、如图是某市“平改坡”工程中一种坡屋顶设计,已知平顶屋面的宽度L为10m,坡屋顶的设计高度h为3.5m,能求斜面钢条a的长度和坡角a。(长度精确到0.1米,角度精确到1°) 在解直角三角形的过程中,常会遇到近似计算,本书除特别说明外,边长保留四个有效数字解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角特别强调:(必须有一个条件是边)练一练1、在Rt△ABC中, a,b,c分别是∠A ,∠B和∠C的对边, ∠C=Rt∠,根据下列条件解直角三角形(边长保留2个有效数字,角度精确到1°)
(1) c=7 ,∠A=36 ° (2)b=10, ∠B=60 °
(3) a=5, c=7 (4)b= , cosA=2、在△ABC中,已知a,b,c分别为∠A,∠B和∠C的对边,∠C=900,根据下列条件解直角三角形(长度保留到2个有效数字,角度精确到1度)(1)c=10,∠A=30°(2)b=4,∠B=72°(3)a=5, c=7练一练(4)a=20,sinA= 如图东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离.(精确到1米)应用练习解 在Rt△ABC中
∵∠CAB=90゜-∠DAC=50゜ 答:敌舰与A、B两炮台的距离分别约为3111米和2384米.∴BC=AB?tan∠CAB
=2000×tan50゜≈2384(米).∴ =tan∠CAB已知解直角三角形a, b∠A, a∠A, ba=b×tanA∠A, Ca=c×sinAb=c×cosA解直角三角形中的边角关系回顾整理 归纳小结1.已知,在△ABC中,∠B=45°,AC=4,BC=2 , 求sinA和AB的值。提高练习2、已知,在△ABC中,∠B=60°,∠C=45°,BC=5㎝。求AB的长。 设x,y都是锐角,下列关系是否成立?如果错误,请举例说明.探究活动:(1)sin2x=2sinx;(2)sinx+cosx<1;(3)当00
sinA=cosB,tanA.tanB=1.特殊角300,450,600角的三角函数值.锐角三角函数同角之间的三角函数关系:
sin2A+cos2A=1.tanA=温故知新01100不存在特殊角的三角函数值回顾互余两角三角函数关系:sin(900-A)=cosAtanAtanB=1cos(900-A)=sinA回顾同角三角函数关系:sin2A+cos2A=1A+B=900引例:山坡上种树,要求株距(相临两树间的水平
距离)是5.5米,测的斜坡倾斜角是24o,求斜坡上相
邻两树间的坡面距离是多少米(精确到0.1米) 解:在Rt△ABC中,∠C=90°引例:山坡上种树,要求株距(相临两树间的水平
距离)是5.5米,测的斜坡倾斜角是24o,求斜坡上相
邻两树间的坡面距离是多少米(精确到0.1米)≈6.0(米)答:斜坡上相邻两树间的坡面距离是6.0米。合作探究1、已知在Rt△ABC中,∠C= Rt∠,AB=5,AC=3,求边BC的长。你能求出∠A的度数么?2、已知在Rt△ABC中, ∠C= Rt∠ ,∠A=560,AB=8,求AC的长。3、如图,在Rt△ABC中,∠C=90°(1)若∠A=30°,BC=2,求AC、AB、∠B(2)若BC=2,AB=4,求AC、∠A、∠B合作探究已知屋面的宽度L和坡顶的设计高度h(如图)。你能求出斜面钢条的长度a和倾角a 吗?想一想变化:已知平顶屋面的宽度L和坡顶的设计倾角α(如图)。你能求出斜面钢条a的长度和设计高度h吗?a 在上述例题中,我们都是利用直角三角形中的已知边、角来求出另外一些的边角.像这样,
******************************** 在直角三角形中,由已知的一些边、角,求出另一些边、角的过程,叫做解直角三角形.解直角三角形1.两锐角之间的关系:2.三边之间的关系:3.边角之间的关系A+B=900a2+b2=c2例1、如图,在Rt△ABC中,∠C=900,∠A=500,AB=3,求∠B和a,b(边长保留2个有效数字)解:Rt△ABC中∠B=900-∠A=400∴a=AB×sinA=3×sin500≈2.3∴b=AB×cosA=3×cos500≈1.9例2、如图是某市“平改坡”工程中一种坡屋顶设计,已知平顶屋面的宽度L为10m,坡屋顶的设计高度h为3.5m,能求斜面钢条a的长度和坡角a。(长度精确到0.1米,角度精确到1°)解:在Rt△ABD中,∴α≈350.答:斜面钢条a的长度约为6.1米,坡角约为350.例2、如图是某市“平改坡”工程中一种坡屋顶设计,已知平顶屋面的宽度L为10m,坡屋顶的设计高度h为3.5m,能求斜面钢条a的长度和坡角a。(长度精确到0.1米,角度精确到1°) 在解直角三角形的过程中,常会遇到近似计算,本书除特别说明外,边长保留四个有效数字解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角特别强调:(必须有一个条件是边)练一练1、在Rt△ABC中, a,b,c分别是∠A ,∠B和∠C的对边, ∠C=Rt∠,根据下列条件解直角三角形(边长保留2个有效数字,角度精确到1°)
(1) c=7 ,∠A=36 ° (2)b=10, ∠B=60 °
(3) a=5, c=7 (4)b= , cosA=2、在△ABC中,已知a,b,c分别为∠A,∠B和∠C的对边,∠C=900,根据下列条件解直角三角形(长度保留到2个有效数字,角度精确到1度)(1)c=10,∠A=30°(2)b=4,∠B=72°(3)a=5, c=7练一练(4)a=20,sinA= 如图东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离.(精确到1米)应用练习解 在Rt△ABC中
∵∠CAB=90゜-∠DAC=50゜ 答:敌舰与A、B两炮台的距离分别约为3111米和2384米.∴BC=AB?tan∠CAB
=2000×tan50゜≈2384(米).∴ =tan∠CAB已知解直角三角形a, b∠A, a∠A, ba=b×tanA∠A, Ca=c×sinAb=c×cosA解直角三角形中的边角关系回顾整理 归纳小结1.已知,在△ABC中,∠B=45°,AC=4,BC=2 , 求sinA和AB的值。提高练习2、已知,在△ABC中,∠B=60°,∠C=45°,BC=5㎝。求AB的长。 设x,y都是锐角,下列关系是否成立?如果错误,请举例说明.探究活动:(1)sin2x=2sinx;(2)sinx+cosx<1;(3)当00
