解直角三角形复习
图片预览

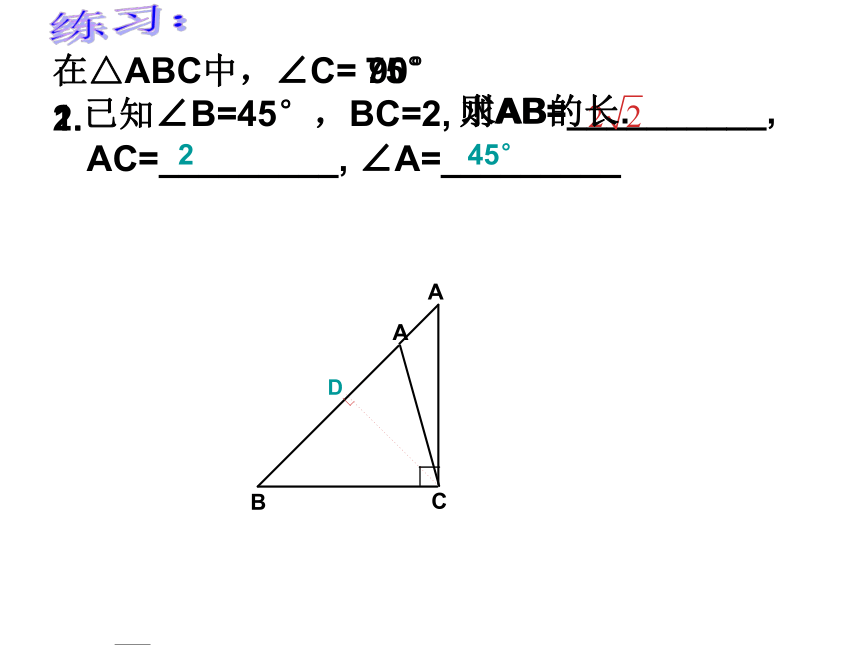
文档简介
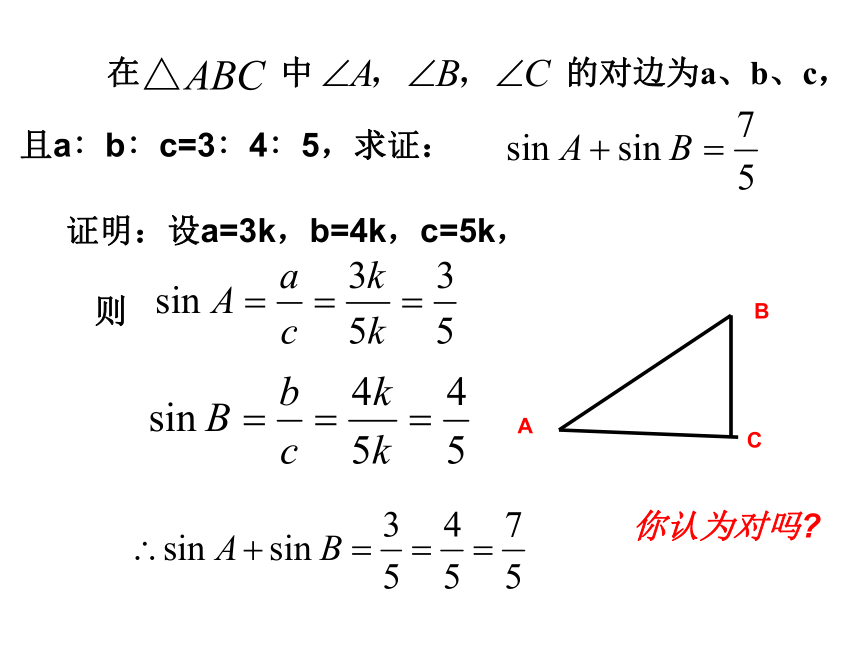
课件17张PPT。 在 中 的对边为a、b、c,且a∶b∶c=3∶4∶5,求证:
证明:设a=3k,b=4k,c=5k,
则
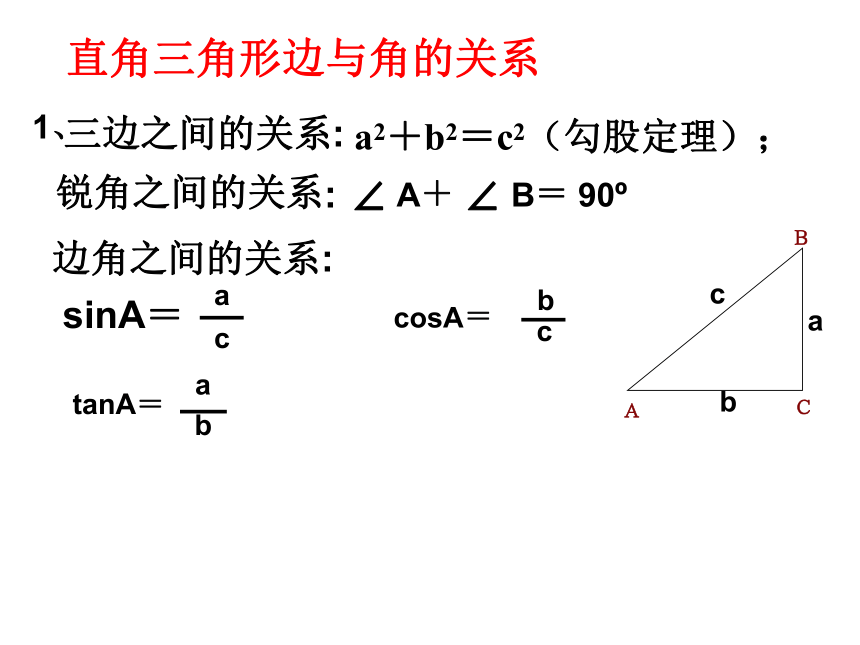
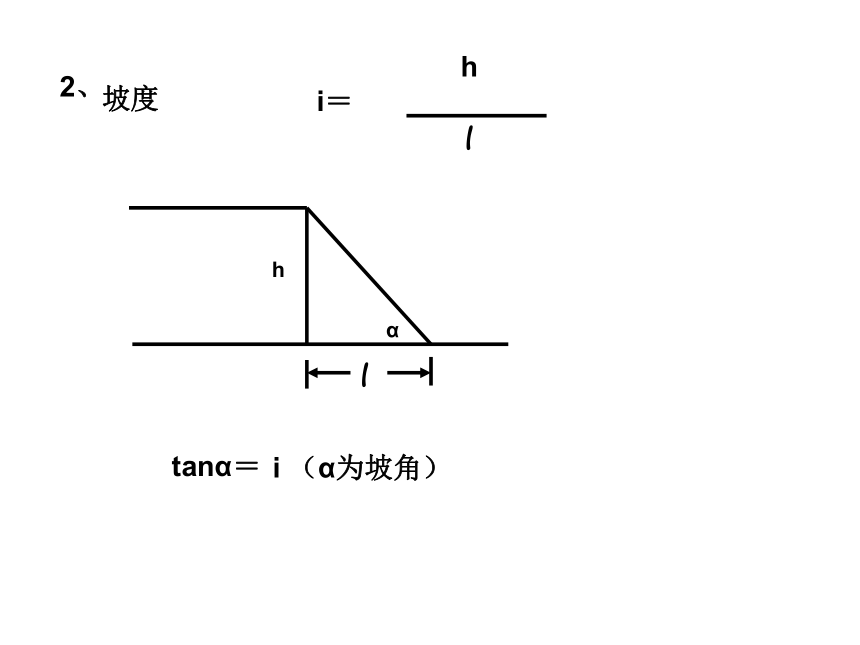
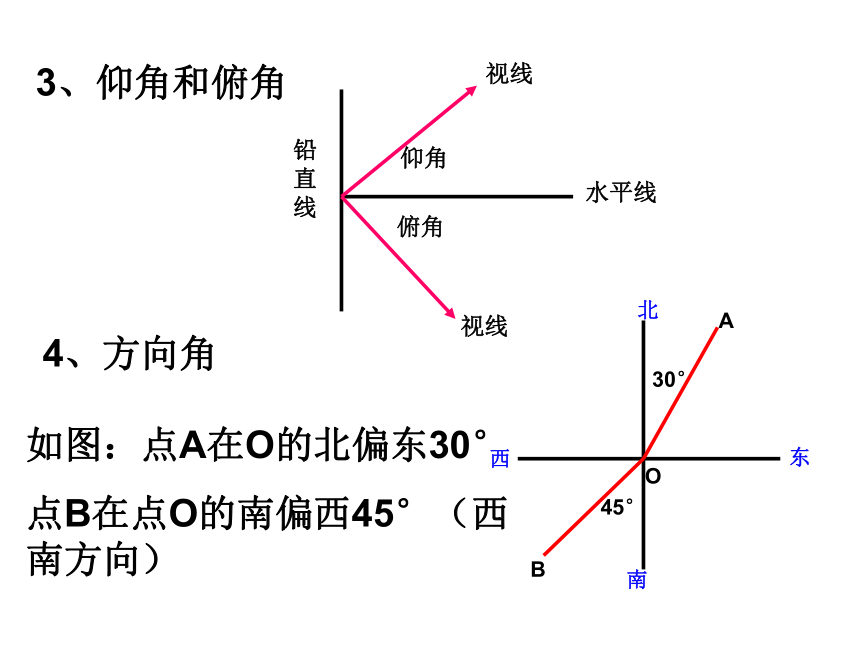
BAC你认为对吗?解直角三角形复习(2)三边之间的关系:a2+b2=c2(勾股定理);锐角之间的关系:∠ A+ ∠ B= 90o边角之间的关系:sinA=直角三角形边与角的关系1、2、3、仰角和俯角4、方向角如图:点A在O的北偏东30°
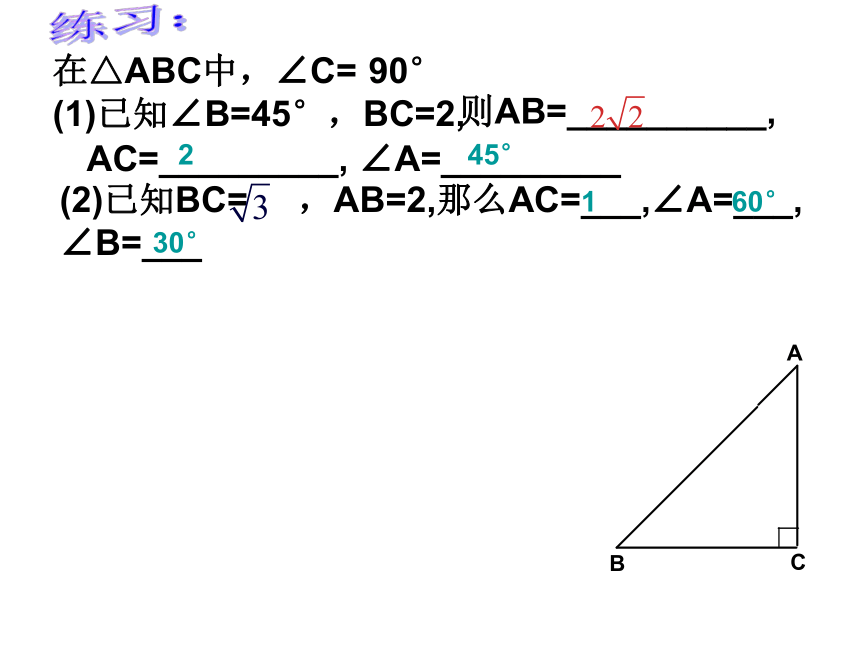
点B在点O的南偏西45°(西南方向)45°则AB=__________, AC=_________, ∠A=_________在△ABC中,∠C=
(1)已知∠B=45°,BC=2, 90°(2)已知BC= ,AB=2,那么AC=___,∠A=___, ∠B=___
2160°30°练习:1.在△ABC中,∠C=
已知∠B=45°,BC=2, 2.D则AB=__________, AC=_________, ∠A=_________90°245°75°求AB的长.练习:例:某海滨浴场的沿岸可以看作直线AC,如图所示,1号救生员在岸边的A点看到海中的B点有人求救,便立即向前跑300米到离B点最近的地点C再跳入海中游到B点救助;若每位救生员在岸上 跑步的速度都是6米/秒,在水中游泳的速度都是2米/秒。D 1. 请问1号救生员的做法是否合理? 2. 若2号救生员从A 跑到D再跳入海中游到B点救助,请问谁先到达B? 如图,为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、C,使得∠ABC=60°,∠ACB=45°,量得BC长为100米,求河的宽度(即求BC边上的高).
D问题1楼房AB的高度是多少?问题2楼房CD的高度是多少?
D1、本节例题学习以后,我们可以得到解直角三角形的两种基本图形:小结:2、注意可解直角三角形与非可解直角三角形的基本解题思路;小提示
1. 应注意锐角三角函数概念的理解领会及运用。
2. 在解直角三角形时应注意原始数据的使
用,不是直角三角形时,可添辅助线(垂线)。
3. 注意数形结合的运用.善于利用方程思想求解 。
4 .使用计算器时,题中没有特别说明,保留4位小数。(08年江苏泰州)如图,某堤坝的横截面是梯形ABCD,背水坡AD的坡度i(即tan)为1︰1.2,坝高为5米。现为了提高堤坝的防洪抗洪能力,市防汛指挥部决定加固堤坝,要求坝顶CD加宽1米,形成新的背水坡EF,其坡度为1︰1.4。已知堤坝总长度为4000米。求完成该工程需要多少土方?(08 山东)如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C.经测量花卉世界D位于点A的北偏东45°方向、点B的北偏东30°方向上,AB=2km,∠DAC=15°.
(1)求B,D之间的距离;
(2)求C,D之间的距离.
你能通过构造直角三角形的方法求出tan15°的精确值吗?
15°
证明:设a=3k,b=4k,c=5k,
则
BAC你认为对吗?解直角三角形复习(2)三边之间的关系:a2+b2=c2(勾股定理);锐角之间的关系:∠ A+ ∠ B= 90o边角之间的关系:sinA=直角三角形边与角的关系1、2、3、仰角和俯角4、方向角如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向)45°则AB=__________, AC=_________, ∠A=_________在△ABC中,∠C=
(1)已知∠B=45°,BC=2, 90°(2)已知BC= ,AB=2,那么AC=___,∠A=___, ∠B=___
2160°30°练习:1.在△ABC中,∠C=
已知∠B=45°,BC=2, 2.D则AB=__________, AC=_________, ∠A=_________90°245°75°求AB的长.练习:例:某海滨浴场的沿岸可以看作直线AC,如图所示,1号救生员在岸边的A点看到海中的B点有人求救,便立即向前跑300米到离B点最近的地点C再跳入海中游到B点救助;若每位救生员在岸上 跑步的速度都是6米/秒,在水中游泳的速度都是2米/秒。D 1. 请问1号救生员的做法是否合理? 2. 若2号救生员从A 跑到D再跳入海中游到B点救助,请问谁先到达B? 如图,为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、C,使得∠ABC=60°,∠ACB=45°,量得BC长为100米,求河的宽度(即求BC边上的高).
D问题1楼房AB的高度是多少?问题2楼房CD的高度是多少?
D1、本节例题学习以后,我们可以得到解直角三角形的两种基本图形:小结:2、注意可解直角三角形与非可解直角三角形的基本解题思路;小提示
1. 应注意锐角三角函数概念的理解领会及运用。
2. 在解直角三角形时应注意原始数据的使
用,不是直角三角形时,可添辅助线(垂线)。
3. 注意数形结合的运用.善于利用方程思想求解 。
4 .使用计算器时,题中没有特别说明,保留4位小数。(08年江苏泰州)如图,某堤坝的横截面是梯形ABCD,背水坡AD的坡度i(即tan)为1︰1.2,坝高为5米。现为了提高堤坝的防洪抗洪能力,市防汛指挥部决定加固堤坝,要求坝顶CD加宽1米,形成新的背水坡EF,其坡度为1︰1.4。已知堤坝总长度为4000米。求完成该工程需要多少土方?(08 山东)如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C.经测量花卉世界D位于点A的北偏东45°方向、点B的北偏东30°方向上,AB=2km,∠DAC=15°.
(1)求B,D之间的距离;
(2)求C,D之间的距离.
你能通过构造直角三角形的方法求出tan15°的精确值吗?
15°
