圆的基本性质回顾（1）

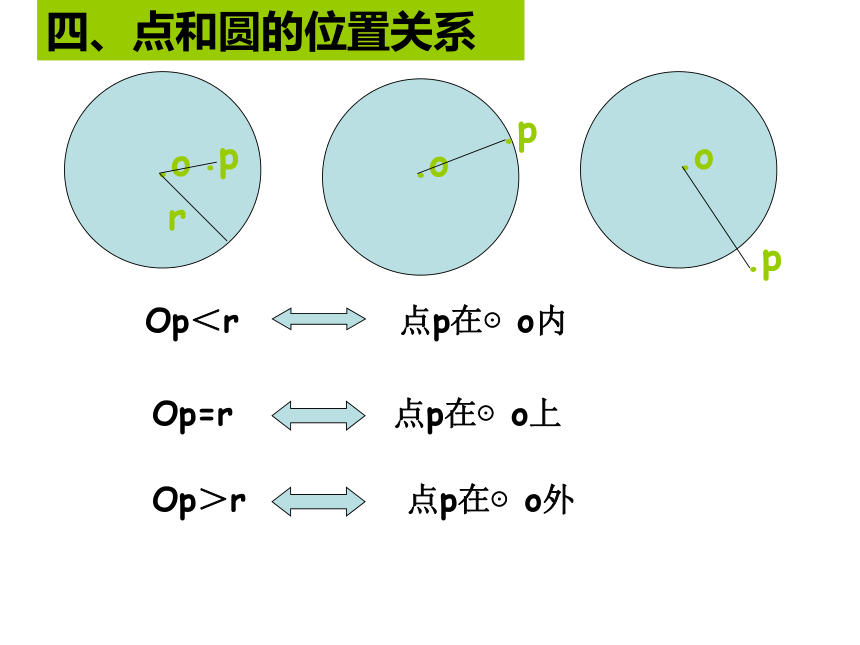
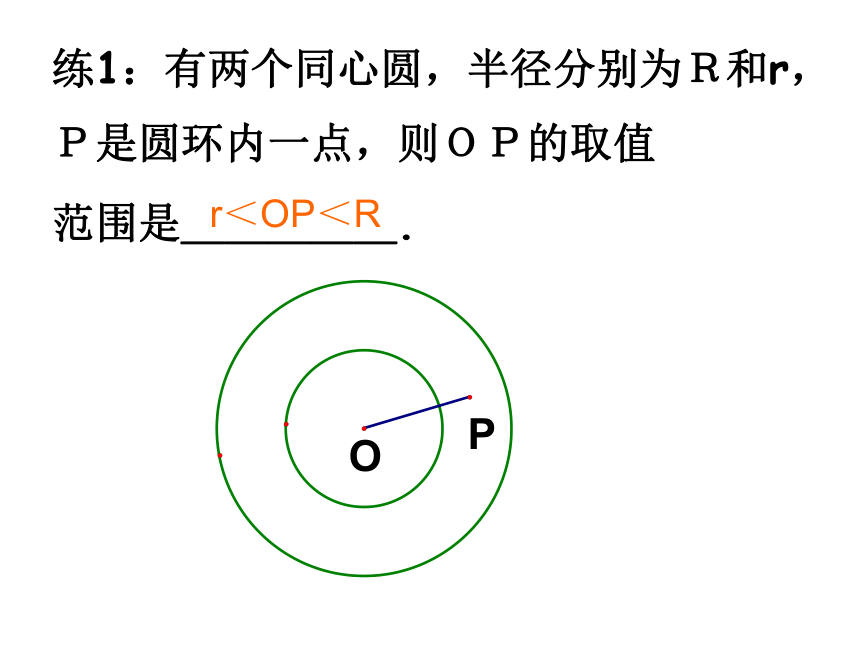
课件18张PPT。圆的基本性质回顾（一）四、点和圆的位置关系练1：有两个同心圆，半径分别为Ｒ和r，
Ｐ是圆环内一点，则ＯＰ的取值
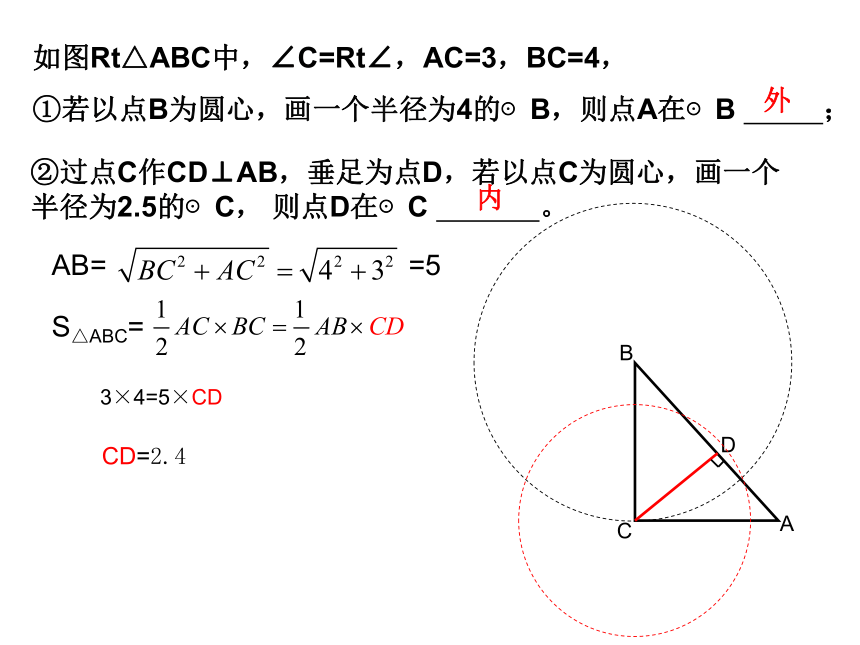
范围是＿＿＿＿＿.r＜OP＜R如图Rt△ABC中，∠C=Rt∠，AC=3，BC=4，
①若以点B为圆心，画一个半径为4的⊙B，则点A在⊙B ；ACBD②过点C作CD⊥AB，垂足为点D，若以点C为圆心，画一个半径为2.5的⊙C， 则点D在⊙C 。
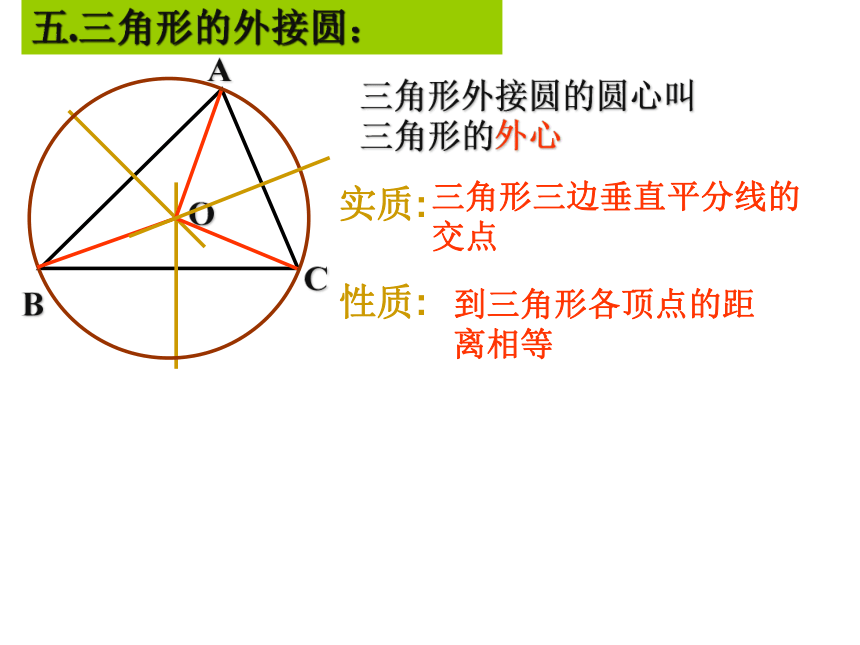
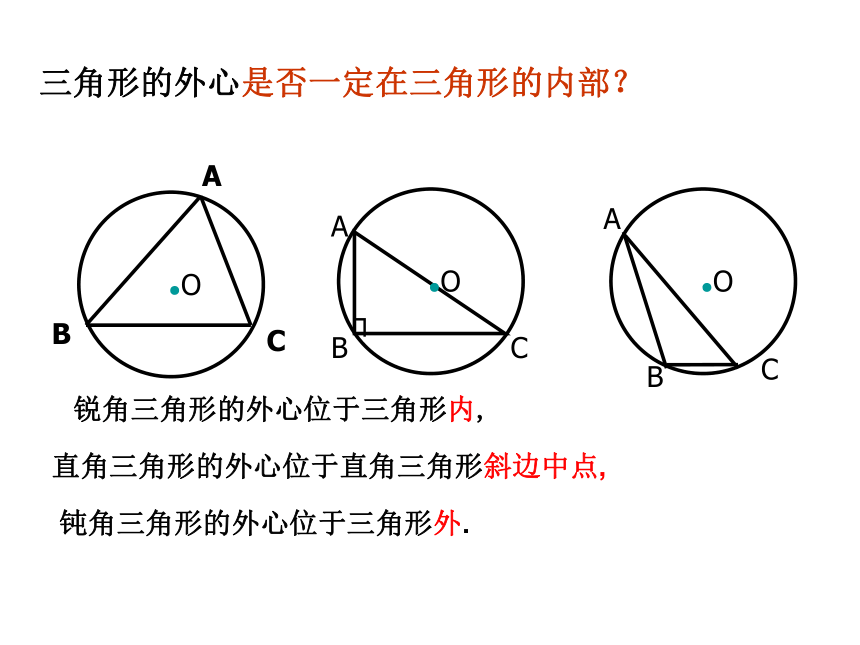
外内AB= =5S△ABC=3×4=5×CDCD=2.4ABCO五.三角形的外接圆：三角形外接圆的圆心叫三角形的外心三角形三边垂直平分线的交点到三角形各顶点的距离相等实质:性质:锐角三角形的外心位于三角形内,三角形的外心是否一定在三角形的内部？直角三角形的外心位于直角三角形斜边中点,钝角三角形的外心位于三角形外.2：已知ABC三点在圆O上，连接ABCO，
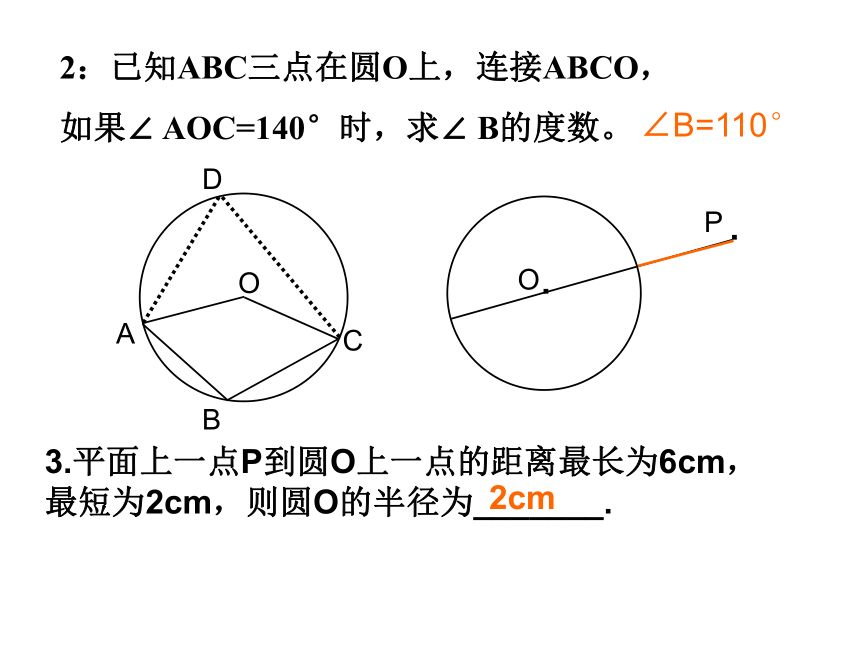
如果∠ AOC=140°时，求∠ B的度数。3.平面上一点P到圆O上一点的距离最长为6cm，
最短为2cm，则圆O的半径为_______.D∠B=110°2cm4.怎样要将一个如图所示的破镜重圆？ABCP5 ： 如图，AB是⊙O的任意一条弦，OC⊥AB，垂足为P，若 CP=7cm，AB=28cm ，你能帮老师求出这面镜子的半径吗？O714设：半径为R，则OP=R－7由勾股定理得：OA2=OP2+AP2即 R2=（R－7）2+142解得：R=17.5
答：镜子的半径为17.5cm一、垂径定理③AM=BM,重视：模型“垂径定理直角三角形” 若 ① CD是直径② CD⊥AB1.定理 垂直于弦的直径平分弦,并且平分
弦所的两条弧.2、垂径定理的逆定理平分弦（不是直径）的直径垂直于弦,并且平 分弦所对的两条弧.垂径定理及推论直径 (过圆心的线) (2)垂直弦
(3) 平分弦 (4)平分弧知二得二注意: “ 直径平分弦则垂直弦.” 这句话对吗?错!ABCD1.两条弦在圆心的同侧ABCD2.两条弦在圆心的两侧例1、⊙O的半径为10cm，弦AB∥CD，
AB=16，CD=12，则AB、CD间的
距离是 .EEFF2或14OF=8OE=6 在同圆或等圆中,如果①两个圆心角,②两条弧,
③两条弦,④两条弦心距中,有一组量相等,那么它们
所对应的其余各组量都分别相等.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′二、圆心角、弧、弦、弦心距的关系圆的对称性圆的轴对称性垂径定理及其推论圆的中心对称性圆心角、弧、弦、弦心距之间的关系总结证明圆弧相等：
（1）定义（2）垂径定理
（3）圆心角、弧、弦、
弦心距之间的关系
证明线段相等：
(1）直线形的方法
（2）垂径定理
（3）圆心角、弧、弦、
弦心距之间的关系
三、圆周角定理及推论 90°的圆周角所对的弦是 .定理: 在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这弧所对的圆心角的一半. 推论:直径所对的圆周角是 .直角直径判断: (1) 相等的圆心角所对的弧相等.
(2)相等的圆周角所对的弧相等.
(3) 等弧所对的圆周角相等.××√6.如图：AB是圆O的直径，BD是圆O的弦，延长BD到C，AC=AB，BD与CD的大小有什么关系？
为什么？若∠B=70度,则∠DOE=＿＿＿.E六、 弧长与扇形面积,圆锥的侧面积与全面积
1. 半径为R的圆中,n°的圆心角所对的弧长的计算公式2. 半径为R的圆中,n°的圆心角所对的扇形面积.3. 圆锥的底面半径为r,母线长为l,高为h