(浙教版八年级上)数学:2.6探索勾股定理(第1课时)课件
文档属性
| 名称 | (浙教版八年级上)数学:2.6探索勾股定理(第1课时)课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-12-06 00:00:00 | ||
图片预览

文档简介
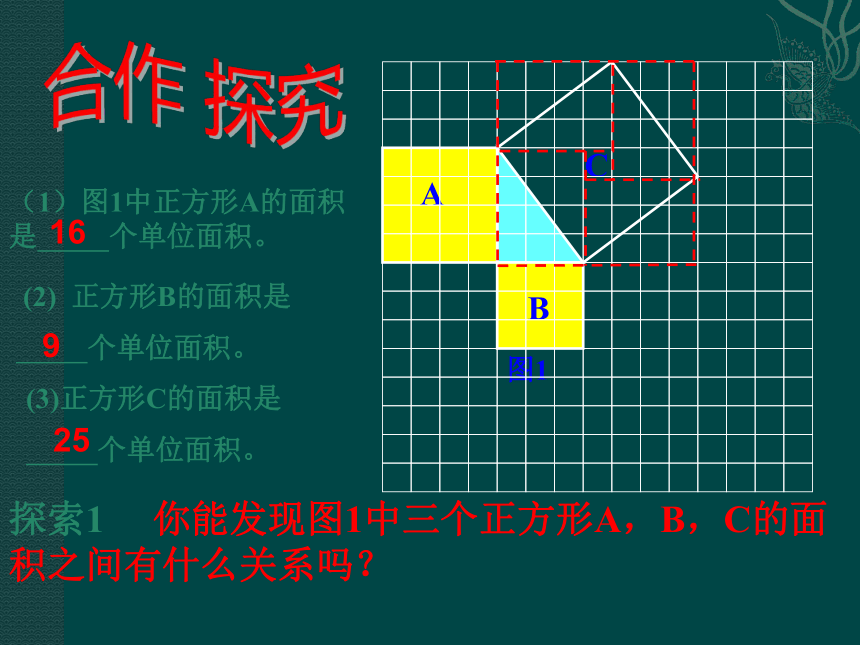
课件17张PPT。2.6 探索勾股定理 (1)勾股定理探索(1)图1中正方形A的面积是 个单位面积。 (2) 正方形B的面积是
个单位面积。(3)正方形C的面积是
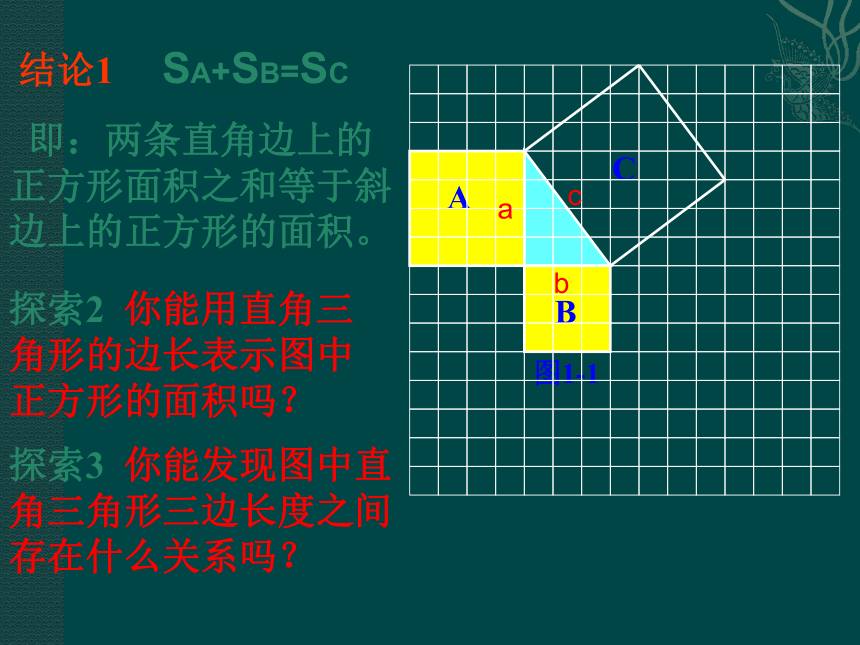
个单位面积。16925合作 探究探索1 你能发现图1中三个正方形A,B,C的面积之间有什么关系吗? 结论1 SA+SB=SC
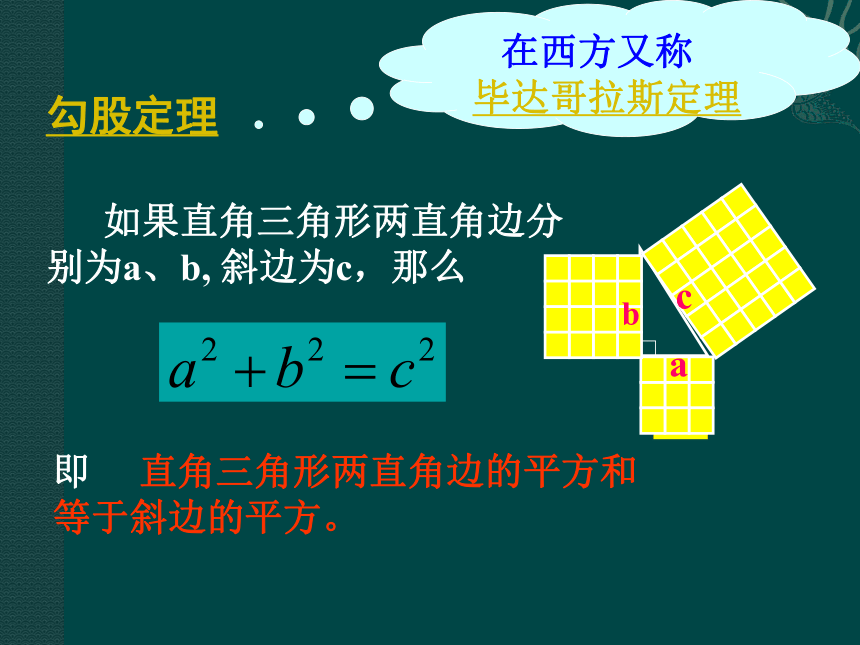
探索2 你能用直角三角形的边长表示图中正方形的面积吗?探索3 你能发现图中直角三角形三边长度之间存在什么关系吗?acb 即:两条直角边上的正方形面积之和等于斜边上的正方形的面积。勾股定理 如果直角三角形两直角边分别为a、b, 斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。abc勾股弦bac2002年国际数学家大会会标赵爽
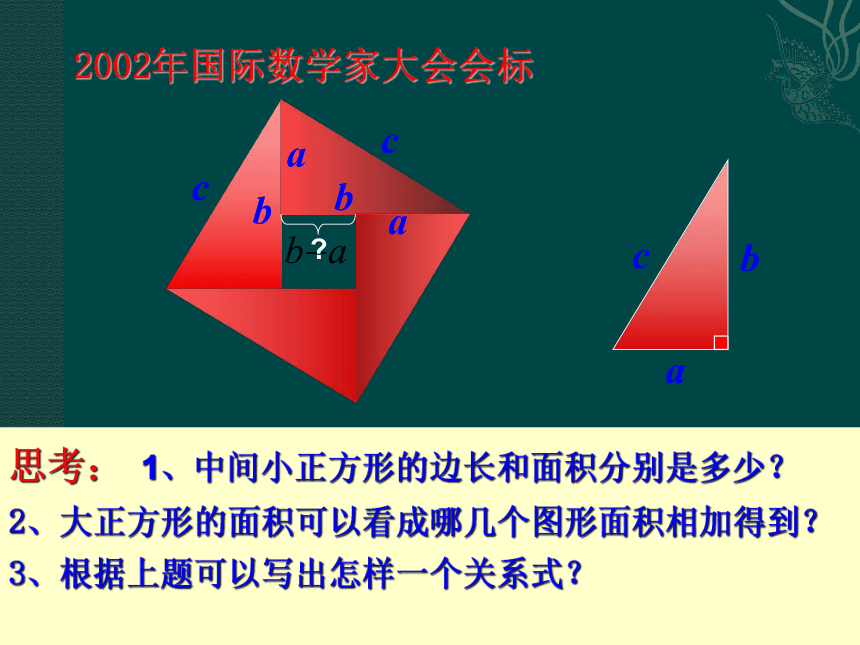
弦图2002年国际数学家大会会标思考: 1、中间小正方形的边长和面积分别是多少?
2、大正方形的面积可以看成哪几个图形面积相加得到?
3、根据上题可以写出怎样一个关系式?
?x例1:如图,你能计算出下列直角三角形中未知边的长吗?2 反思:若要你在数轴上准确表示 ,你会参考上面的结果画吗?小结:利用勾股定理可以解决直角三角形的边长。121x83x5x例题精练解:由勾股定理得x2=12+22=5∵x>0
∴x=(1)直角三角形的两直角边为3和4,则斜边为___(3)直角三角形的两直角边为6和8,则斜边为___(2)直角三角形的两直角边为5和12,则斜边为___比一比谁最快(5)直角三角形的两条边为3和4,则斜边上的高是 。(4)直角三角形的两条边为3和4,则这个直角三角形的周长为 。12或51013例2:一个长方形零件图,根据所给的尺寸(单位mm),求两孔中心A、B之间的距离.C解:过A作铅垂线,过B作水平线,两线交于点C,则∠ACB=90°AC=90-40=50(mm)由勾股定理,得∵AB﹥0, ∴AB=130(mm)答:两孔中心A、B之间的距离为130mm。 构造直角三角形可以解决实际问题。BC=160-40=120(mm)501201.小刚想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触到地面,你能计算旗杆的高度是多少米吗?试 一 试2.一架云梯长25米,斜靠在墙上,梯子低端距离墙7米远,
(1)求梯上顶端距地面垂直高度为多少米?
(2)如果梯子顶端下滑了4米,那么梯子底部在水平方向也滑动了4米吗?请你仔细算一算。说说这节课你的收获和体会
让大家与你一起分享体会 . 分享作业1、再次阅读课本
2、完成作业本 中国最早的一部数学著作《周髀(bì) 算经》中记录着在公元前1100年左右的西周时期数学家商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。” 后来人们就简单地把这个事实说成“勾三股四弦五”。这就是著名的勾股定理。
在稍后一点的《九章算术》( 约在 公元50至100年间)一书中,勾股定理得到了更加规范的一般性表达。书中的《勾股章》说:“把勾和股分别自乘,然后把它们的积加起来,再进行开方,便可以得到弦。”
我国最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽。毕达哥拉斯 在国外,相传勾股定理是公元前550年时古希腊数学家兼哲学家毕达哥拉斯首先发现的。因此又称此定理为“毕达哥拉斯定理”。但毕达哥拉斯对勾股定理的证明方法已经失传。且他发现的时间比我国要迟得多。
个单位面积。(3)正方形C的面积是
个单位面积。16925合作 探究探索1 你能发现图1中三个正方形A,B,C的面积之间有什么关系吗? 结论1 SA+SB=SC
探索2 你能用直角三角形的边长表示图中正方形的面积吗?探索3 你能发现图中直角三角形三边长度之间存在什么关系吗?acb 即:两条直角边上的正方形面积之和等于斜边上的正方形的面积。勾股定理 如果直角三角形两直角边分别为a、b, 斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。abc勾股弦bac2002年国际数学家大会会标赵爽
弦图2002年国际数学家大会会标思考: 1、中间小正方形的边长和面积分别是多少?
2、大正方形的面积可以看成哪几个图形面积相加得到?
3、根据上题可以写出怎样一个关系式?
?x例1:如图,你能计算出下列直角三角形中未知边的长吗?2 反思:若要你在数轴上准确表示 ,你会参考上面的结果画吗?小结:利用勾股定理可以解决直角三角形的边长。121x83x5x例题精练解:由勾股定理得x2=12+22=5∵x>0
∴x=(1)直角三角形的两直角边为3和4,则斜边为___(3)直角三角形的两直角边为6和8,则斜边为___(2)直角三角形的两直角边为5和12,则斜边为___比一比谁最快(5)直角三角形的两条边为3和4,则斜边上的高是 。(4)直角三角形的两条边为3和4,则这个直角三角形的周长为 。12或51013例2:一个长方形零件图,根据所给的尺寸(单位mm),求两孔中心A、B之间的距离.C解:过A作铅垂线,过B作水平线,两线交于点C,则∠ACB=90°AC=90-40=50(mm)由勾股定理,得∵AB﹥0, ∴AB=130(mm)答:两孔中心A、B之间的距离为130mm。 构造直角三角形可以解决实际问题。BC=160-40=120(mm)501201.小刚想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触到地面,你能计算旗杆的高度是多少米吗?试 一 试2.一架云梯长25米,斜靠在墙上,梯子低端距离墙7米远,
(1)求梯上顶端距地面垂直高度为多少米?
(2)如果梯子顶端下滑了4米,那么梯子底部在水平方向也滑动了4米吗?请你仔细算一算。说说这节课你的收获和体会
让大家与你一起分享体会 . 分享作业1、再次阅读课本
2、完成作业本 中国最早的一部数学著作《周髀(bì) 算经》中记录着在公元前1100年左右的西周时期数学家商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。” 后来人们就简单地把这个事实说成“勾三股四弦五”。这就是著名的勾股定理。
在稍后一点的《九章算术》( 约在 公元50至100年间)一书中,勾股定理得到了更加规范的一般性表达。书中的《勾股章》说:“把勾和股分别自乘,然后把它们的积加起来,再进行开方,便可以得到弦。”
我国最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽。毕达哥拉斯 在国外,相传勾股定理是公元前550年时古希腊数学家兼哲学家毕达哥拉斯首先发现的。因此又称此定理为“毕达哥拉斯定理”。但毕达哥拉斯对勾股定理的证明方法已经失传。且他发现的时间比我国要迟得多。
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
