5.2不等式的基本性质

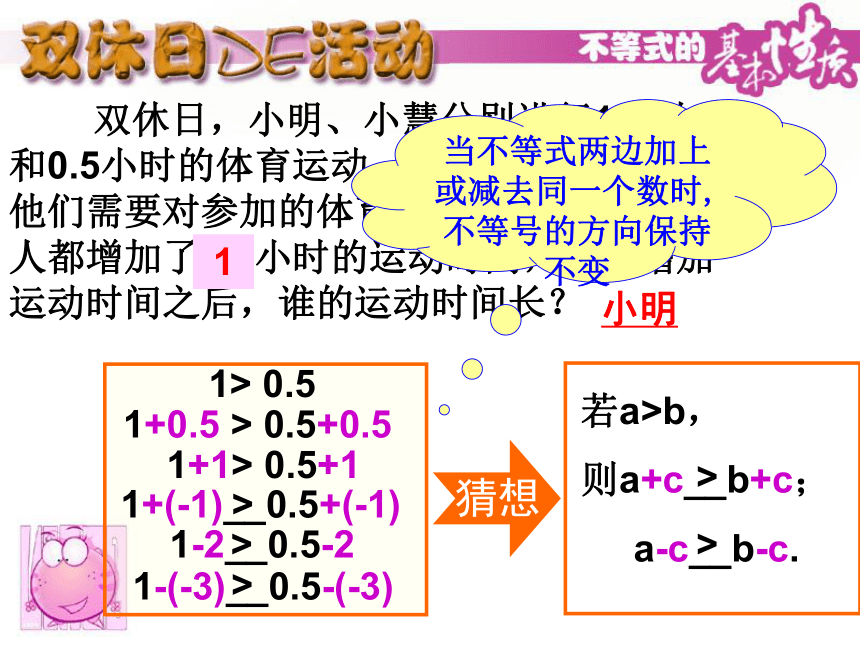
课件30张PPT。同学们，让我们一起乘坐幸福快车，领略一路的数学美景！执教：邓美芬5.2不等式的基本性质 双休日，小明进行上网、学习、体育运动的时间分别为a小时、b小时、c小时. 已知a 不等式的传递性． 双休日，小明、小慧分别进行1小时和0.5小时的体育运动. 由于运动会临近，他们需要对参加的体育项目进行训练，两人都增加了0.5小时的运动时间，请问增加运动时间之后，谁的运动时间长？小明1+0.5 > 0.5+0.51+1> 0.5+11> 0.5>>>1若a>b，
则a+c__b+c；
a-c__b-c.>>猜想当不等式两边加上或减去同一个数时,不等号的方向保持不变cccc把a>b表示在数轴上，不妨设c>0∴a+c>b+c∴a-c>b-c　　不等式的两边都加上（或都减去）同一个数，所得到的不等式仍成立.如果a＞b，那么a+c＞b+c，a-c＞b-c；
如果a＜b，那么a+c＜b+c，a-c＜b-c.即选择适当的不等号填空，并说明理由.>≥≥ 比较下列大小8＿＿12
8×4＿＿12×4
8÷4＿＿12÷4
8×(－4)＿＿12×(－4)
8÷(－4)＿＿12÷(－4)＜＜＜＞＞想一想：从上面的变化,，你发现了什么?探索学习当不等式的两边都乘或都除以同一个正数时,不等号的方向不变,而都乘或都除以同一个负数时,不等号的方向改变. 不等式的两边都乘（或都除以）同一个正数，所得的不等式仍成立; 不等式的两边都乘（或都除以）同一个负数，必须把不等号的方向改变，所得的不等式仍成立.如果a＞b，且c＞0，那么ac＞bc， ＞ ；
如果a＞b，且c＜0，那么ac＜bc， ＜ ；即选择适当的不等号填空，并说明理由.>>>不等式的基本性质1：
若a＜b，b＜c，则a＜c。
不等式的基本性质2：
如果a＞b，那么a+c＞b+c，a-c＞b-c.
如果a＜b，那么a+c＜b+c，a-c＜b-c.
不等式的基本性质3：
如果a＞b，且c＞0，那么ac＞bc，a÷c＞b÷c.
如果a＞b，且c＜0，那么ac＜bc，a÷c＜b÷c.知识归纳若a＜b，b＜c，则a＜c如果a＞b,那么
a+c＞b+c，a-c＞b-c 如果a=b,那么a+c=b+c,a-c=b-c若a=b,b=c,则a=c等式与不等式的基本性质的区别与联系小试牛刀崭露头角初出茅庐（1）若x+1>0，两边同加上-1，
得_________
（依据：_______________）；
（2）若 x≤ ，两边同乘-3，
得 _________
（依据：________________）. x>-1不等式的基本性质2不等式的基本性质3x≥填空：（1）若a>-b，则a+b____0；
（2）若a<选择适当的不等号填空，并说明理由.（1）若-a（2）若a>0，且(b-1)a<0，则b____1.选择适当的不等号填空，并说明理由.><已知a<0，试比较2a与a的大小.解法二：在数轴上分别表示2a和a的点（a<0）, 如图2a位于a的左边，∴2a ∴2a＜a（不等式的基本性质3）解法三：∵ a＜0,
∴ a+a ＜ a
∴2a ∵ 2a-a=a, 又∵ a＜0,
∴ 2a-a＜0，∴2a0时,
当a=0时,
当a<0时, 例12a>a2a=a=02ay，比较2-3x与2-3y的大小，并说明理由.解：∵x>y∴-3x<-3y（不等式的基本性质3）∴2-3x<2-3y（不等式的基本性质2）小试牛刀崭露头角锋芒毕露初出茅庐百尺竿头大显身手解：设计算机键盘的单价为x元，60≤X≤70∴180≤3X≤210 某品牌计算机键盘的单价在60元至70元之间（包括60元，70元），买3个这样的键盘需要多少钱（用适当的不等式表示）？由题意得：若x>y，且(a-3)x<(a-3)y，
求a的取值范围.解：∵x>y，且(a-3)x<(a-3)y，∴a-3<0（不等式的基本性质3）∴a<3（不等式的基本性质2）若x>y，请比较(a-3)x与(a-3)y的大小.变式训练解：当a>3时，当a＝3时，当a＜3时，　　某商场有A、B两款服装，A款服装价格超过B款服装价格的1倍以上；国庆期间，商场开展了促销活动，这两款服装的价格都下调了15%. 你认为价格下调之后，A款服装价格仍超过B款服装价格的1倍以上吗？请说明理由.解：设A、B两款服装的原价分别为a元、b元. 由题意得， a>2b. 国庆期间，A、B两款服装的价格分别为 (1-15%)a元、 (1-15%)b元. ∵1-15%>0， ∴(1-15%)a>2(1-15%)b. 即价格下调之后，A款服装价格仍超过B款服装价格的1倍以上. 恭喜你们，闯关成功！畅所欲言作业:作业本 5.2 再见