寻找相似三角形

课件15张PPT。相似三角形的复习 杨斌
长兴实验初级中学
复习基础：相似三角形基本模型：∵DE//BC
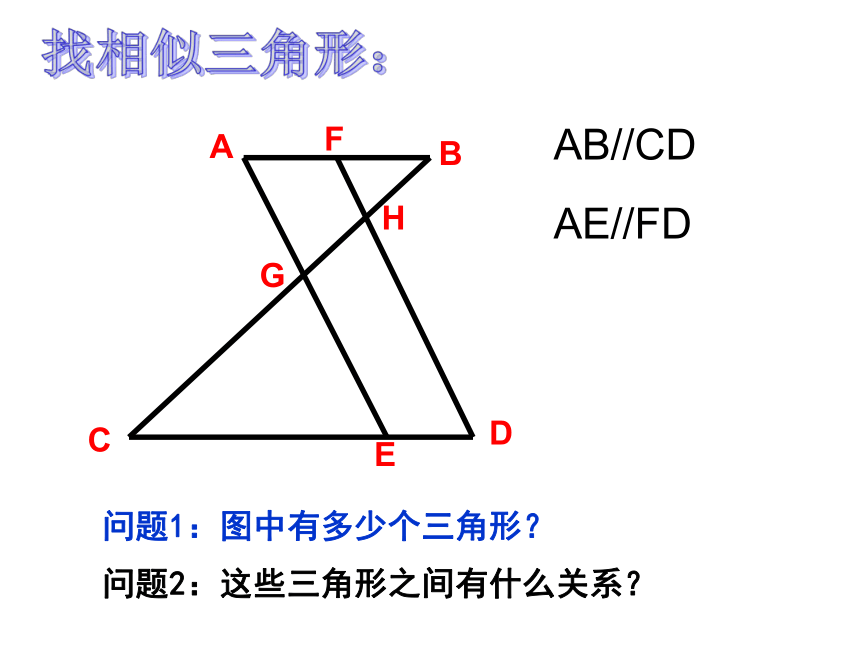
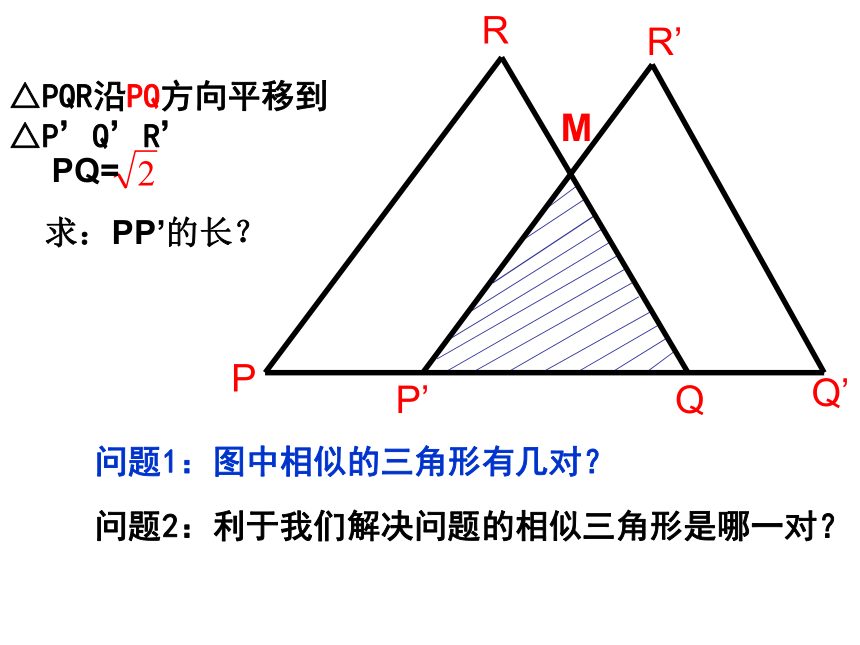
∴△ADE∽△ABCBAFCGEHDAB//CDAE//FD问题1：图中有多少个三角形？问题2：这些三角形之间有什么关系？找相似三角形：问题1：图中相似的三角形有几对？△PQR沿PQ方向平移到△P’Q’R’M问题2：利于我们解决问题的相似三角形是哪一对？PQ=求：PP’的长？PENMQ问题1：图中有几对
相似三角形？问题2：连结MN，
若QN平分∠ MNP,
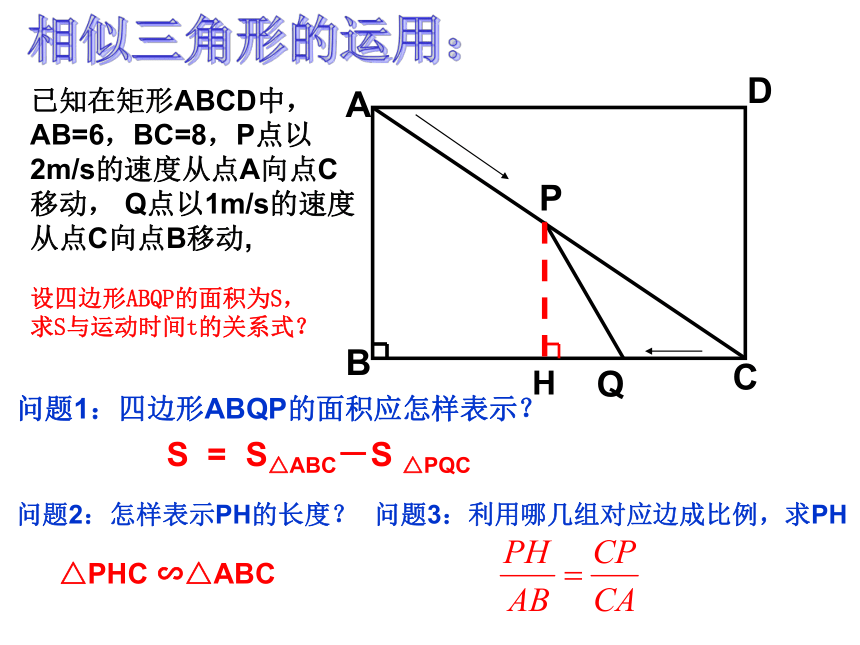
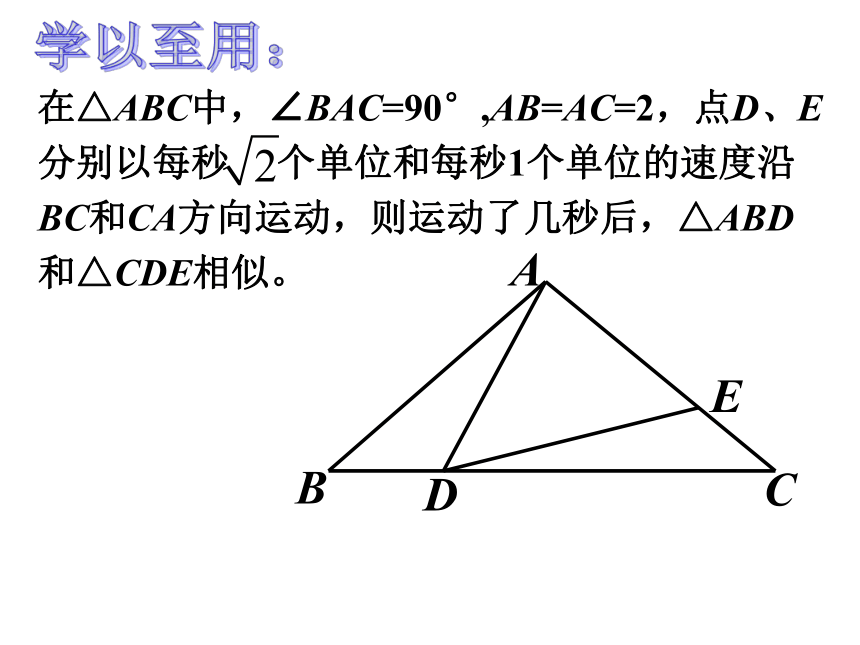
则图中相似的三角形有几对？问题3：连结PQ，图中的三角形相似又有几对？△MEQ ∽△NEP△MEQ ∽△NEP△MEQ ∽△NMQ△NMQ ∽△NEP△ MEQ ∽△NEP∽△NMQ△ QNP ∽△QPE∽△MNEH已知在矩形ABCD中，AB=6，BC=8，P点以2m/s的速度从点A向点C移动， Q点以1m/s的速度从点C向点B移动,设四边形ABQP的面积为S，求S与运动时间t的关系式？问题1：四边形ABQP的面积应怎样表示？问题2：怎样表示PH的长度？S = S△ABC－S △PQC△PHC ∽△ABC问题3：利用哪几组对应边成比例，求PH相似三角形的运用：在△ABC中，∠BAC=90°,AB=AC=2，点D、E分别以每秒 个单位和每秒1个单位的速度沿BC和CA方向运动，则运动了几秒后，△ABD和△CDE相似。学以至用：BADCEF1.已知在矩形ABCD中，AB=6，BC=8，若把矩形对折，点A、C恰好重合，折痕为EF，求EF的长？O做一做：2.如图正方形ABCD中，点E为BC的中点，CM⊥DE,垂足为点M，则CBMEDA小结：正确的思考方法是解决问题的关键3.如图，AB⊥DB于点B ，CD⊥DB于点D，AB=4，CD=3，BD=8.
问：在DB上是否存在P点，使以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似？如果存在，计算出点P的位置；如果不存在，请说明理由。如图，DC=3,DB=8,若点P是DB上一动点,
连接CP 过点P作PE⊥CP，交射线BA于点
E,设DP=x，BE=y，
求y关于x的函数关系式.xy△CPE能否成为等腰三角形？如果能，求出DP的长，如果不能，请说明理由。四边形CDBE能否构成矩形？如果能，求出DP的长；如果不能，请说明理由；在上图中，连结CE，当点P运动到何处时,
△ CDP ∽ △ CPE 当点P运动到何处时四边形CDBE的面积最大？
如图，已知抛物线与x轴交A,B两点，与y轴交于C点，抛物线上有一点P，满足∠PBC=90°，求点P的坐标；
ABP1COxyX=423Q6P2