相似三角形的复习
图片预览



文档简介
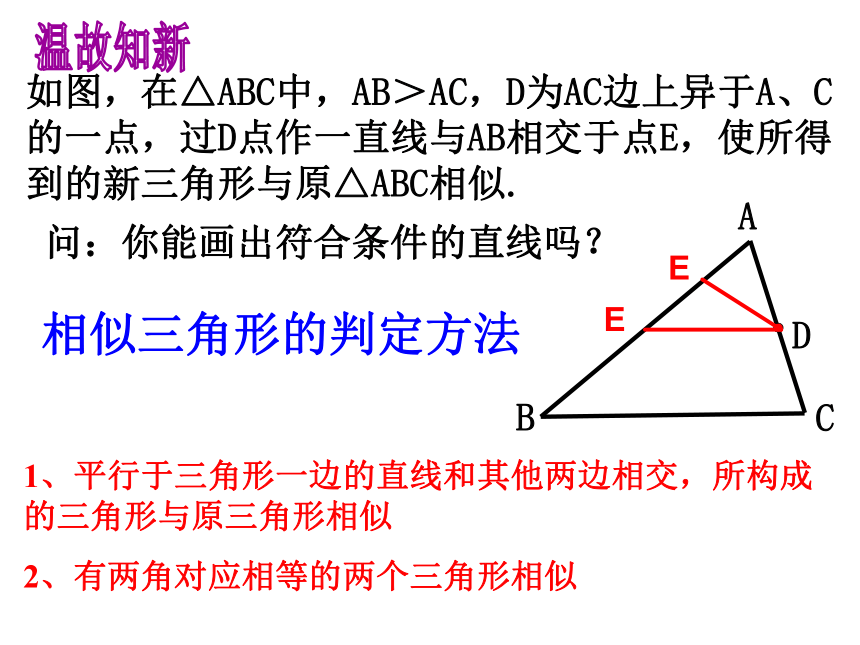
课件15张PPT。如图,在△ABC中,AB>AC,D为AC边上异于A、C的一点,过D点作一直线与AB相交于点E,使所得到的新三角形与原△ABC相似.问:你能画出符合条件的直线吗?
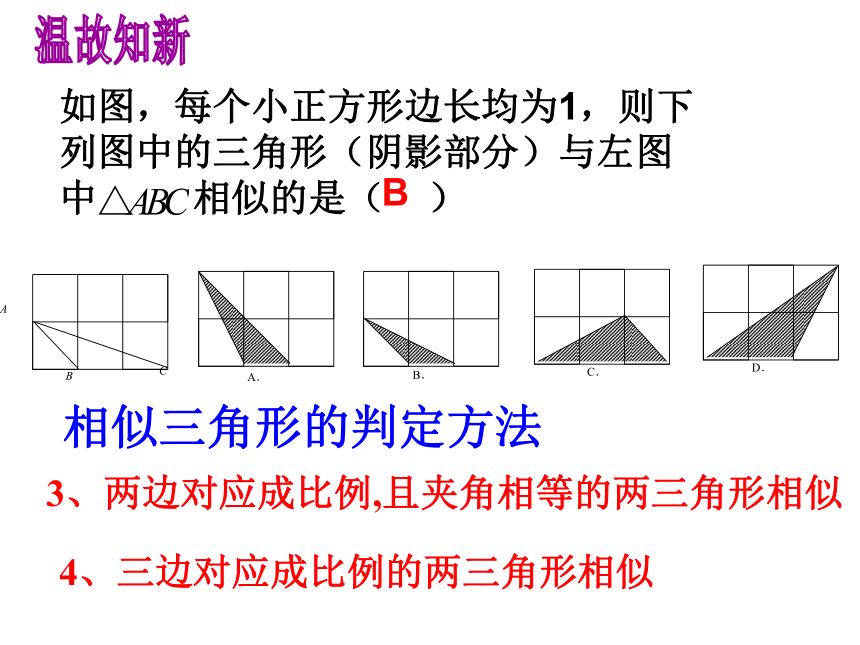
温故知新 EE相似三角形的判定方法1、平行于三角形一边的直线和其他两边相交,所构成 的三角形与原三角形相似2、有两角对应相等的两个三角形相似如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与左图中 相似的是( )3、两边对应成比例,且夹角相等的两三角形相似4、三边对应成比例的两三角形相似B相似三角形的判定方法温故知新 1、平行于三角形一边的直线和其他两边相 交,所构成的三角形与原三角形相似
2、有两角对应相等的两个三角形相似
3、两边对应成比例,且夹角相等的两个三角形相似
4、三边对应成比例的两个三角形相似相似三角形的判定方法1、 已知,D、E为△ABC中BC、AC上两点,CE=3,CA=8,CB=6, 若∠CDE=∠A,
则:CD=_____,
△CDE的周长:△CAB的周长 = _______,
△CDE的面积:△CAB的面积=______.
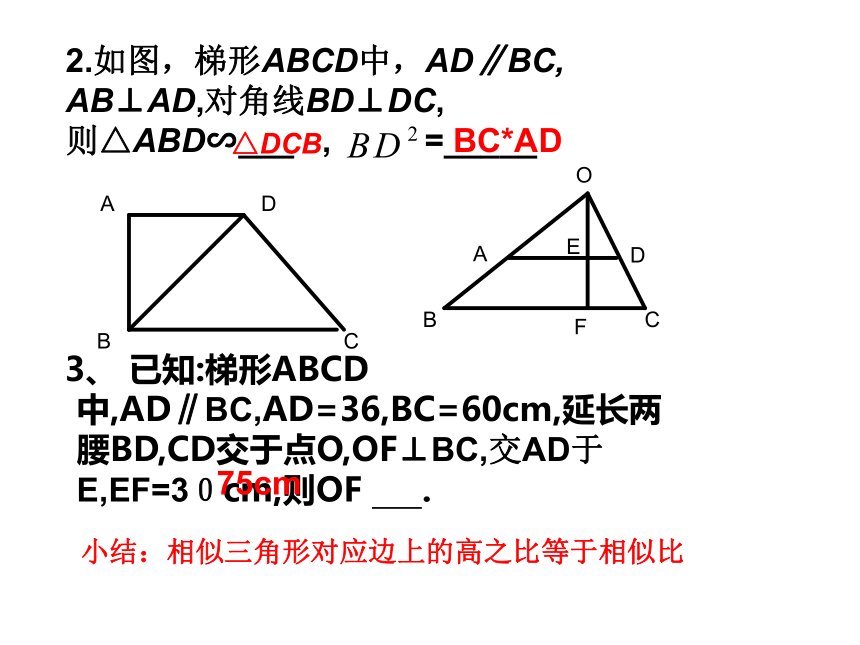
41:21:4试一试,你一定能行小结:相似三角形对应边成比 例,周长比等于相似比,面积比等于相似比的平方2.如图,梯形ABCD中,AD∥BC,
AB⊥AD,对角线BD⊥DC,
则△ABD∽___ , =_____ 3、 已知:梯形ABCD 中,AD∥BC,AD=36,BC=60cm,延长两腰BD,CD交于点O,OF⊥BC,交AD于E,EF=30cm,则OF .
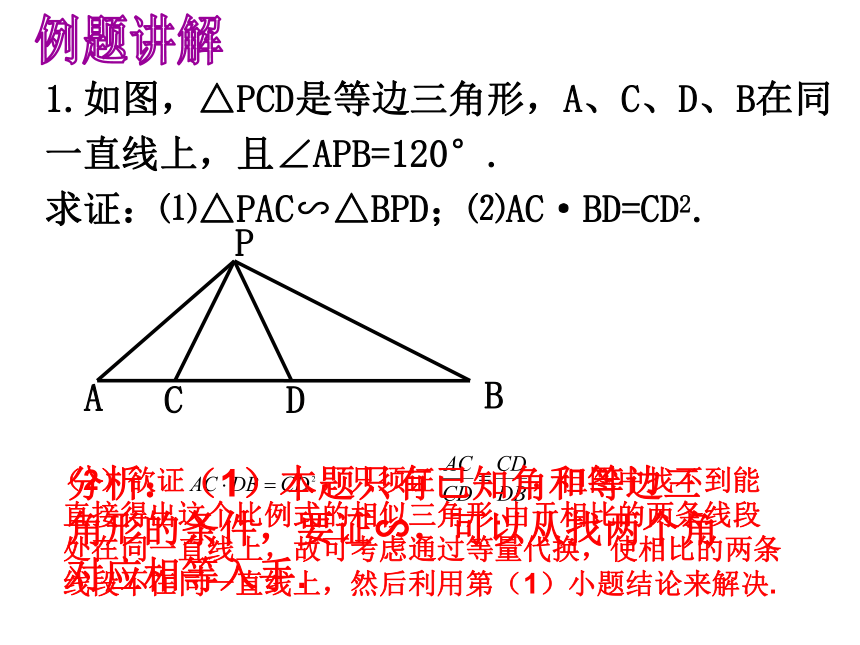
△DCBBC*AD75cm小结:相似三角形对应边上的高之比等于相似比1.如图,△PCD是等边三角形,A、C、D、B在同
一直线上,且∠APB=120°.
求证:⑴△PAC∽△BPD;⑵AC·BD=CD2. 例题讲解分析:(1)本题只有已知角和等边三角形的条件,要证∽,可以从找两个角对应相等入手.知识应用1.如图,已知△PAC∽△QCB ,
△PCQ是等边三角形
(1)求∠ACB的度数.
(2)求证:AC2=AP·AB.例2如图,在△ABC中, CA=4,CB=3,AB=5,当DE∥AB,动点D在BC上(与B、C不重合),E点在AC上.(1)当△CED的面积与四边形EABD的面积相等时,求CD的长.DE∥AB △CED ∽△CABCB=3,CD= ,S △CAB分析过程例2如图,在△ABC中, CA=4,CB=3,AB=5,当DE∥AB,动点D在BC上(与B、C不重合),E点在AC上.(2)当△CED的周长与四边形EABD的周长相等时,求CD的长.DE∥AB △CED ∽△CABCE:CA=CD:CB, 设CD=X
CE= ,C △CAB=6分析过程 例2、如图,在△ABC中, CA=4,CB=3,AB=5,当DE∥AB,动点D在BC上(与B、C不重合),E点在AC上.(3)试问在AB上是否存在点P,使得△EDP
为等腰直角三角形?如果存在,请求出DE的长;如果不存在,请简要说明理由。分类讨论思想
1、以ED为腰
2、以ED为底提示:相似三角形对应边上的高之比等于相似比已知:如图,D在△ABC的边AC上,且DE∥BC,
交AB于E,F在AE上,且AE2=AF×AB,
求证: △AFD∽ △AEC.尝试练习这节课你有什么收获?2、相似三角形判定和性质的应用3、方程思想、分类讨论思想的应用1、复习相似三角形的判定和性质谢谢,再见! 4、如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°(1)求证:△ABD∽△DCE(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时AE取得最小值(3)当△ADE是等腰三角形时,求AE的长拓展提高1
温故知新 EE相似三角形的判定方法1、平行于三角形一边的直线和其他两边相交,所构成 的三角形与原三角形相似2、有两角对应相等的两个三角形相似如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与左图中 相似的是( )3、两边对应成比例,且夹角相等的两三角形相似4、三边对应成比例的两三角形相似B相似三角形的判定方法温故知新 1、平行于三角形一边的直线和其他两边相 交,所构成的三角形与原三角形相似
2、有两角对应相等的两个三角形相似
3、两边对应成比例,且夹角相等的两个三角形相似
4、三边对应成比例的两个三角形相似相似三角形的判定方法1、 已知,D、E为△ABC中BC、AC上两点,CE=3,CA=8,CB=6, 若∠CDE=∠A,
则:CD=_____,
△CDE的周长:△CAB的周长 = _______,
△CDE的面积:△CAB的面积=______.
41:21:4试一试,你一定能行小结:相似三角形对应边成比 例,周长比等于相似比,面积比等于相似比的平方2.如图,梯形ABCD中,AD∥BC,
AB⊥AD,对角线BD⊥DC,
则△ABD∽___ , =_____ 3、 已知:梯形ABCD 中,AD∥BC,AD=36,BC=60cm,延长两腰BD,CD交于点O,OF⊥BC,交AD于E,EF=30cm,则OF .
△DCBBC*AD75cm小结:相似三角形对应边上的高之比等于相似比1.如图,△PCD是等边三角形,A、C、D、B在同
一直线上,且∠APB=120°.
求证:⑴△PAC∽△BPD;⑵AC·BD=CD2. 例题讲解分析:(1)本题只有已知角和等边三角形的条件,要证∽,可以从找两个角对应相等入手.知识应用1.如图,已知△PAC∽△QCB ,
△PCQ是等边三角形
(1)求∠ACB的度数.
(2)求证:AC2=AP·AB.例2如图,在△ABC中, CA=4,CB=3,AB=5,当DE∥AB,动点D在BC上(与B、C不重合),E点在AC上.(1)当△CED的面积与四边形EABD的面积相等时,求CD的长.DE∥AB △CED ∽△CABCB=3,CD= ,S △CAB分析过程例2如图,在△ABC中, CA=4,CB=3,AB=5,当DE∥AB,动点D在BC上(与B、C不重合),E点在AC上.(2)当△CED的周长与四边形EABD的周长相等时,求CD的长.DE∥AB △CED ∽△CABCE:CA=CD:CB, 设CD=X
CE= ,C △CAB=6分析过程 例2、如图,在△ABC中, CA=4,CB=3,AB=5,当DE∥AB,动点D在BC上(与B、C不重合),E点在AC上.(3)试问在AB上是否存在点P,使得△EDP
为等腰直角三角形?如果存在,请求出DE的长;如果不存在,请简要说明理由。分类讨论思想
1、以ED为腰
2、以ED为底提示:相似三角形对应边上的高之比等于相似比已知:如图,D在△ABC的边AC上,且DE∥BC,
交AB于E,F在AE上,且AE2=AF×AB,
求证: △AFD∽ △AEC.尝试练习这节课你有什么收获?2、相似三角形判定和性质的应用3、方程思想、分类讨论思想的应用1、复习相似三角形的判定和性质谢谢,再见! 4、如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°(1)求证:△ABD∽△DCE(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时AE取得最小值(3)当△ADE是等腰三角形时,求AE的长拓展提高1
同课章节目录
