4.6图形位似
图片预览


文档简介
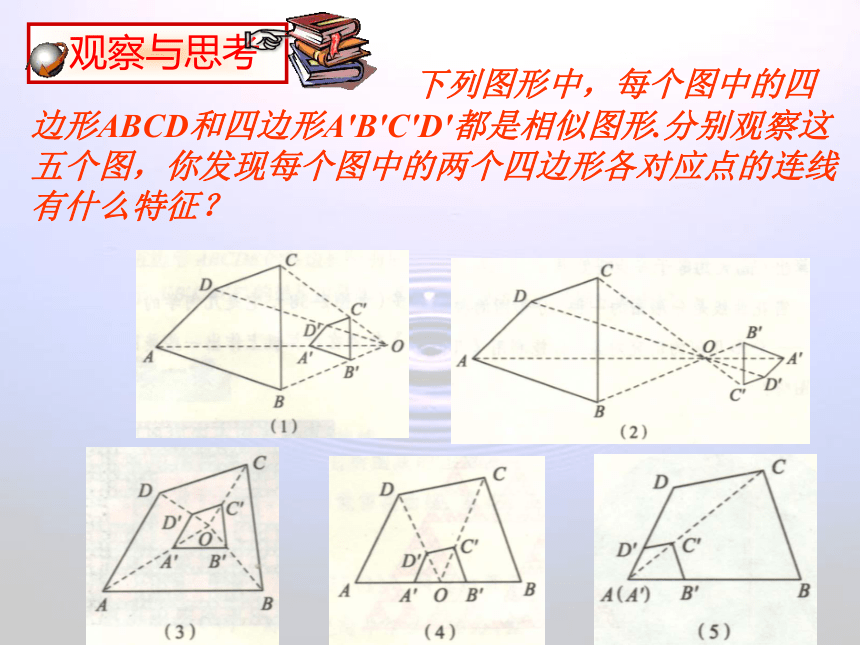
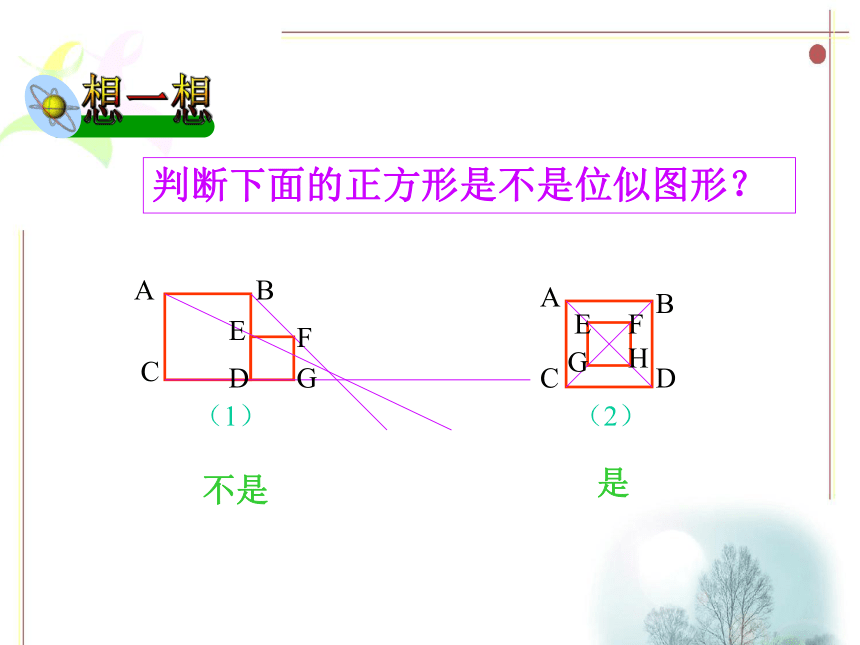
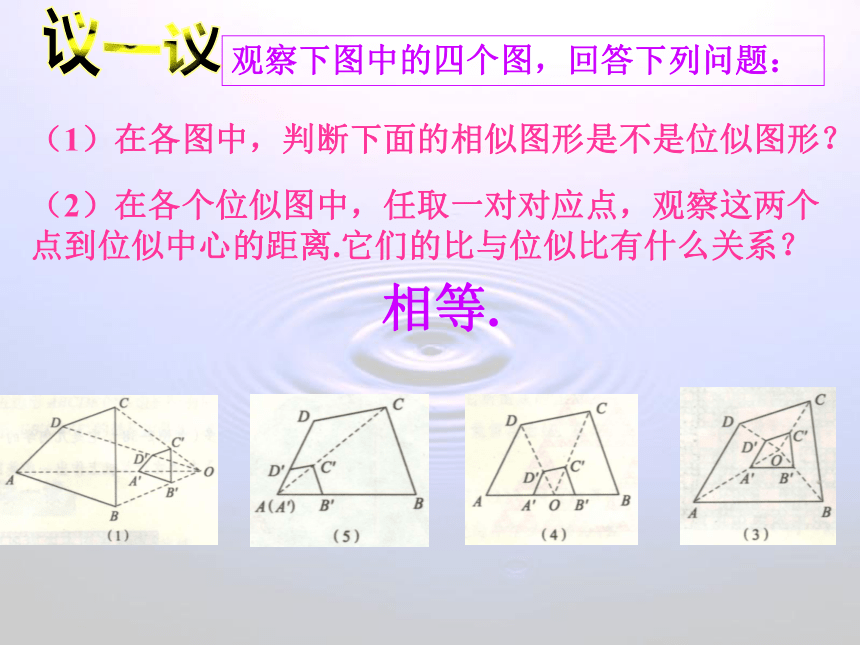
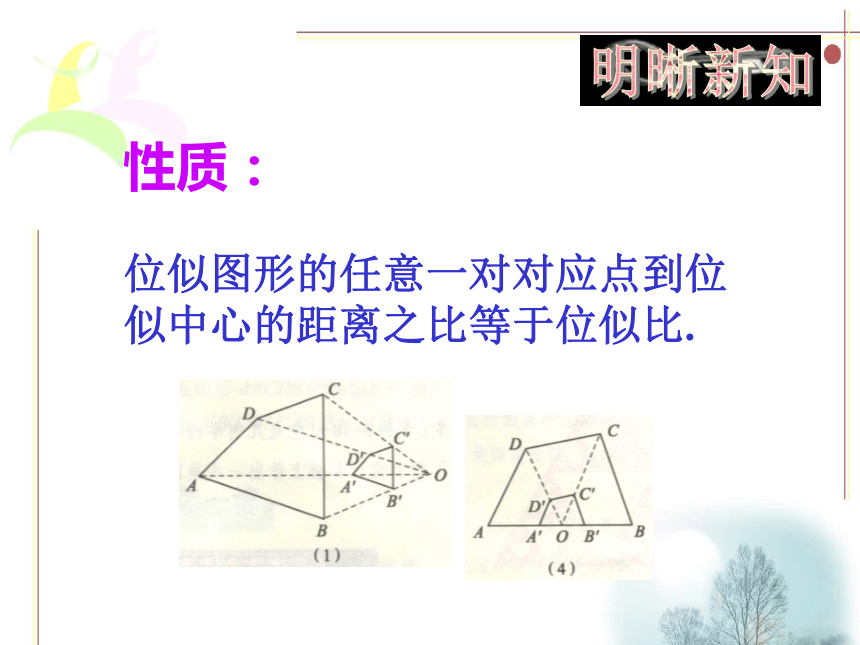
课件12张PPT。4.6 图形的位似龙湖镇中 蔡永洧 下列图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图,你发现每个图中的两个四边形各对应点的连线有什么特征?如果两个相似图形的每组对应点所在的直线都交于一点,那么这样的两个图形叫做位似图形, 这个交点叫做位似中心, 这时两个相似图形的相似比又叫做它们的位似比.判断下面的正方形是不是位似图形?(1)(2)不是是ACDBCBADFEGGFEH议一议观察下图中的四个图,回答下列问题:(1)在各图中,判断下面的相似图形是不是位似图形?(2)在各个位似图中,任取一对对应点,观察这两个点到位似中心的距离.它们的比与位似比有什么关系?相等.性质:
位似图形的任意一对对应点到位似中心的距离之比等于位似比. 例: 如图,请以坐标原点O为位似中心,作它的位似图形,并把的边长放大3倍. 作位似图形 如果两个相似图形的每组对应点所在的直线都交于一点,那么这样的两个图形叫做位似图形, 这个交点叫做位似中心概念:请观察各对对应点的坐标?已知:像与原像的相似比为3。写出下面的坐标。
A( , ) E( , ) M( , )
B( , ) F( , ) N( , )
C( , ) G( , ) P( , )
D( , ) H( , )Q( , )MQPN0 4 0 12 0 -12 2 0 6 0 -6 0 6 0 18 0 -18 0 4 4 12 12 -12 -12 如果原图象上的坐标为(x,y).像与原像的位似比为k,那么像上的对应点的坐标为( , )或( , ) kx ky -kx -ky练一练:1.如图:已知三角形ABC和点O。以点O为位似中心,求作三角形ABC的位似图形,并把他的边长缩小到原来的一半。OACB2. 在直角坐标系中,三角形ABC的各个顶点坐标如图。现在要以坐标原点O为位似中心,作出像与原像 的位似比为2/3的新图形 并说出各个对应点的坐标。练一练:通过这节课的学习,你有哪些收获?课堂小结1.如果两个相似图形的每组对应点所在的直线都交于一点,那么这样的两个图形叫做位似图形, 这个交点叫做位似中心, 这时两个相似图形的相似比又叫做它们的位似比.2.位似图形的任意一对对应点到位似中心的距离之比等于位似比.3.如何作位似图形课后作业:1.课后习题
2.作业本
位似图形的任意一对对应点到位似中心的距离之比等于位似比. 例: 如图,请以坐标原点O为位似中心,作它的位似图形,并把的边长放大3倍. 作位似图形 如果两个相似图形的每组对应点所在的直线都交于一点,那么这样的两个图形叫做位似图形, 这个交点叫做位似中心概念:请观察各对对应点的坐标?已知:像与原像的相似比为3。写出下面的坐标。
A( , ) E( , ) M( , )
B( , ) F( , ) N( , )
C( , ) G( , ) P( , )
D( , ) H( , )Q( , )MQPN0 4 0 12 0 -12 2 0 6 0 -6 0 6 0 18 0 -18 0 4 4 12 12 -12 -12 如果原图象上的坐标为(x,y).像与原像的位似比为k,那么像上的对应点的坐标为( , )或( , ) kx ky -kx -ky练一练:1.如图:已知三角形ABC和点O。以点O为位似中心,求作三角形ABC的位似图形,并把他的边长缩小到原来的一半。OACB2. 在直角坐标系中,三角形ABC的各个顶点坐标如图。现在要以坐标原点O为位似中心,作出像与原像 的位似比为2/3的新图形 并说出各个对应点的坐标。练一练:通过这节课的学习,你有哪些收获?课堂小结1.如果两个相似图形的每组对应点所在的直线都交于一点,那么这样的两个图形叫做位似图形, 这个交点叫做位似中心, 这时两个相似图形的相似比又叫做它们的位似比.2.位似图形的任意一对对应点到位似中心的距离之比等于位似比.3.如何作位似图形课后作业:1.课后习题
2.作业本
同课章节目录
