7.4 一次函数的图象(2)

课件29张PPT。 7.4一次函数的图象(2)一条直线 2、一次函数y=kx+b的图象是 __________3、作一次函数图象时,只要确定__ _个点 两 4、图象上一个点的坐标是
( , ) 自变量取一值相应的函数值复习回顾这条直线与坐标轴的交点坐标为(0，b），（ ，0）1、作函数图象的方法是 ；
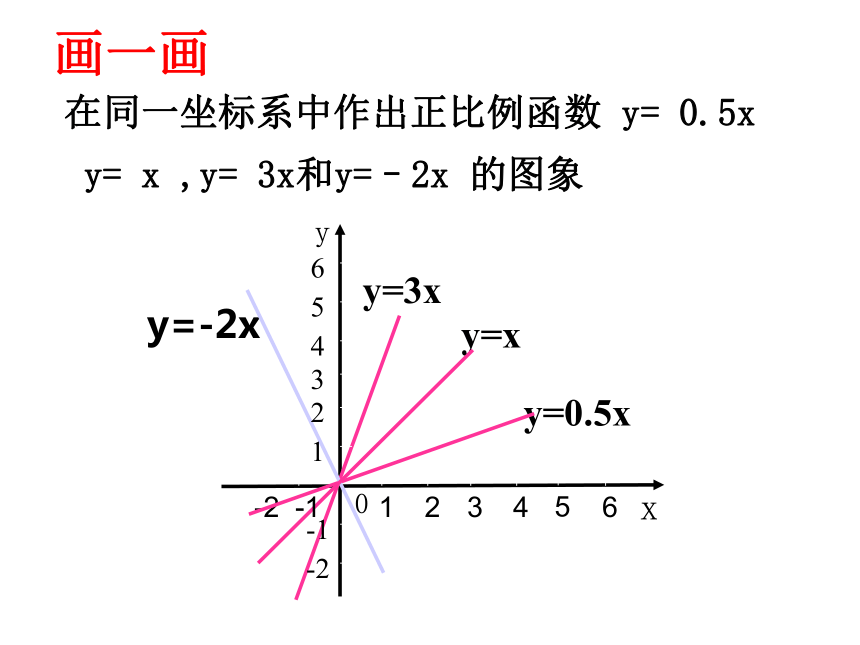
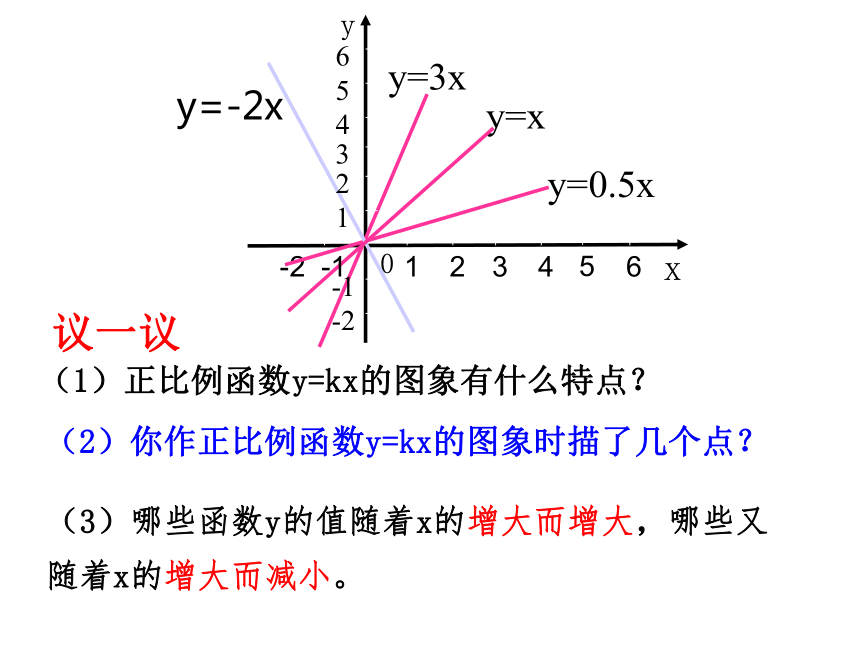
步骤是 ， ， 。列表描点描点法连线 在同一坐标系中作出正比例函数 y= 0.5x
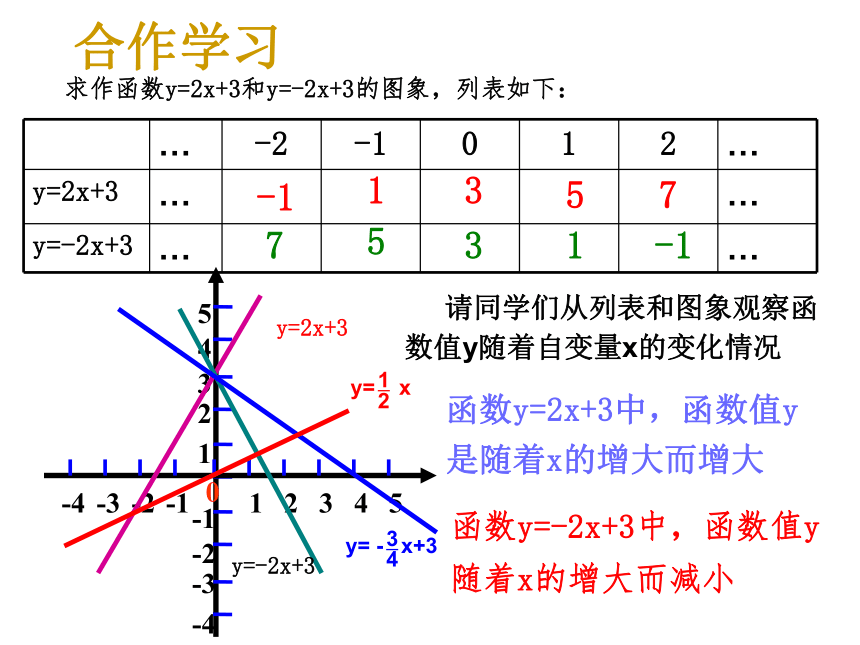
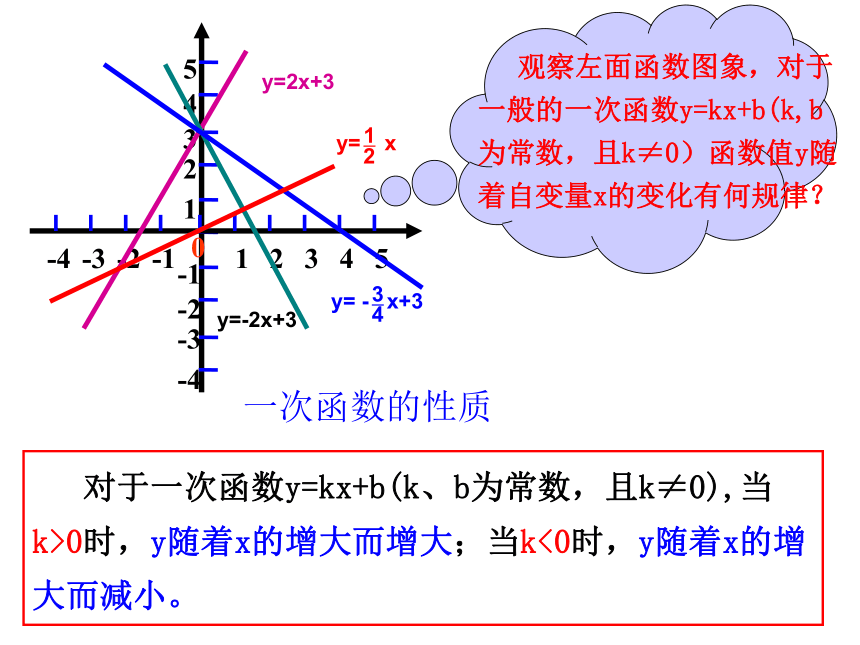
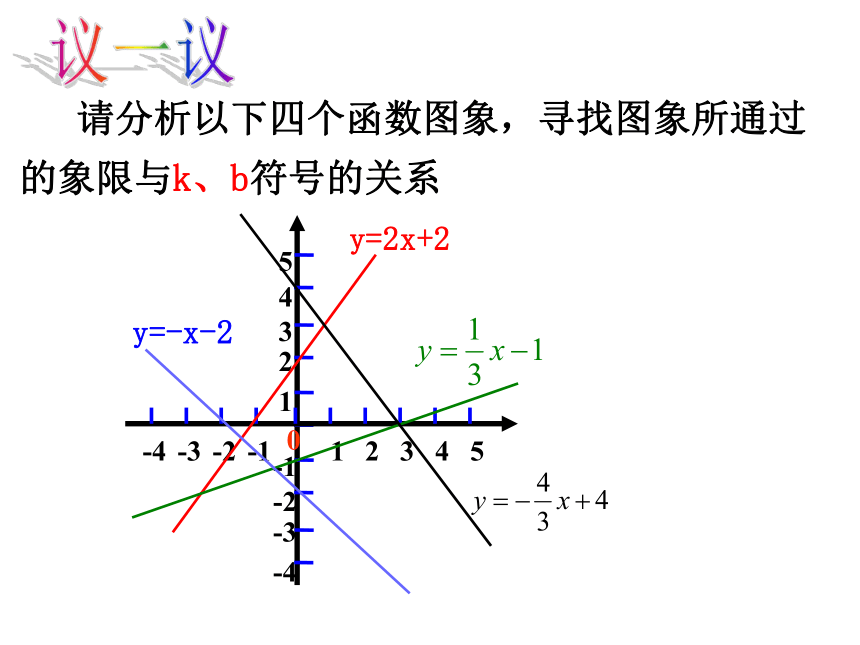
y= x ,y= 3x和y=–2x 的图象 画一画（1）正比例函数y=kx的图象有什么特点？ 议一议（3）哪些函数y的值随着x的增大而增大，哪些又随着x的增大而减小。（2）你作正比例函数y=kx的图象时描了几个点？求作函数y=2x+3和y=-2x+3的图象，列表如下：y=2x+3y=-2x+3 请同学们从列表和图象观察函数值y随着自变量x的变化情况-113577531-1函数y=2x+3中，函数值y是随着x的增大而增大函数y=-2x+3中，函数值y随着x的增大而减小合作学习一次函数的性质 对于一次函数y=kx+b(k、b为常数，且k≠0),当k>0时，y随着x的增大而增大；当k<0时，y随着x的增大而减小。y=2x+3y=-2x+3 请分析以下四个函数图象，寻找图象所通过的象限与k、b符号的关系议一议当k>0,b>0时图象经过一、二、三象限当k>0,b<0时图象经过一、三、四象限当k<0,b>0时图象经过一、二、四象限当k<0,b<0时图象经过二、三、四象限特别地当k>0,b=0时图象经过一、三象限当k<0,b=0时图象经过二、四象限对于一次函数y=kx+b(k≠0,k,b为常数)，其图象与k、b的关系有以下规律：重要结论2.y=-2x-3的图象经过 象限。3.一次函数y=4x+b的图象有两点A（-1，y1）,
B（2，y2),则y1 y2<一、三、四二、三、四4、设下列两个函数当 时， ； 当 时， 。用“>”或“<”号填空： （1）对于函数 ，若 则（2）对于函数 ，若 则1.y=4x-3的图象经过 象限。做一做 >5.下列函数,y的值随着x值的增大如何变化？ 增大增大减小减小做一做例1、已知一次函数 的函数值y随自变量x的增大而减小，求m的取值范围。新知运用解：由已知得：3+2m＜0∴m＜-1.50 ∴s随着p的增大而增大∵ 6100≤P≤6200∴6×6100+120000≤s≤6×6200+120000即：156600≤s≤157200答:6年后该地区的造林面积达到15.66～15.72万公顷.则 S=6P+120000 我国已知某种商品的买入价为30元，售出价的10%用于缴税和其他费用。若要使纯利润保持在买入价的11%~20%之间（包话11%和20%），问怎样确定售出价？设纯利润为y，售出价为x，得y=0.9x-30由题意得：30×11%≤0.9x-30≤30×20%37≤x≤40课内练习2例3、要从甲、乙两仓库向A、B两工地运送水泥，已知甲仓库可运出100吨水泥，乙仓库可运出80吨水泥；A工地需70吨水泥，B工地需110吨水泥，两仓库到A，B两工地的路程和每吨每千米的运费如下表：(1)设甲仓库运往A地水泥x吨,求总运费y关于x的函数解析式,并画出图象; 分析：1、总运费为:甲仓→A地的运费甲仓→Ｂ地的运费乙仓→Ａ地的运费乙仓→Ｂ地的运费２、每个仓库到各地的运费怎么计算呢？路程×运费单价×运量3、上面的三个量已知的是　　　　 　　　， 需要表示的是　　　　　　　　。　　路程运费单价运 量(1)设甲仓库运往A地水泥x吨,求总运费y关于x的函数解析式,并画出图象; 解（1）各仓库运出的水泥吨数和运费如下表：x70-x100-x10+x1.2×20x1.2×15×(70-x)1×25(100-x)0.8×20×(10+x)所以y关于x的函数关系式是y=－3x+3920 (0≤x≤70).y=1.2×20x+1×25×(100-x)+1.2×15×(70-x)+0.8×20[110-(100-x)] 将x=70代入表中的各式可知，当甲仓向Ａ，Ｂ两工地各运送７０吨和３０吨，乙仓库不向Ａ工地运送水泥，而只向Ｂ工地运送８０吨时，总运费最省，最省的总运费为：
-３×70+3920=3710(元）(2)当甲、乙两仓库各运往A，B两工地多少吨水泥时，总运费最省？最省的总运费是多少？这个坐标系有什么特别的地方吗？4000所以y关于x的函数关系式是：y=－3x+3920 (0≤x≤70) 它的图象是直线吗？怎么画？（２）利用一次函数的增减性．★ 当自变量在一定范围内取值时，求一次函数的最大值与最小值有哪些方法？（１）利用图象，（2）当甲、乙仓库各运往A、B两工地多少吨水泥时，总运费最省？解：在一次函数y=-3x+3920 中，K<0 所以y随着x的增大而减小因为0≤x≤70 ，所以当 x = 70 时，y的值最小 当x = 70 时，y = -3 x +3920 = -3×70+3920=3710(元） 答：当甲仓库向A工地运送70吨水泥，则他向B工地运送30吨水泥；乙仓库不向A工地运送水泥，而只向B工地运送80吨时，总运费最省利用一次函数的增减性． 为了清洗水箱，需放掉水箱内原有的200升水，若8:00打开放水龙头，放水的速度为2升/分，运用函数解析式和图象解答以下问题：（1）估计8:55~9:05（包括8:55和9:05）水箱内还剩多少升水；（2）当水箱中存水少于10升时，放水时间已经超过多少分？解:(1) y表示放水X(分)时,
水箱内水的升数,由题意,得y =200-2x (55≤x≤65)则 70≤ y ≤90 如图:(2)放水时间超过95分.课内练习3注意完全平方公式和平方差公式不同：对于一次函数y=kx+b（k，b为常数，且k≠0）
当k﹥0时，y随x的增大而增大；
当k﹤0时，y随x的增大而减小。 基本方法: (1)图象法;
(2)解析法:解一元一次不等式(组)3.利用图象和性质解决简单的问题1.一次函数的性质2.会根据自变量的取值范围,求一次函数的取值范围小 结作业：1、复习、整理、巩固今天所学知识。
2、作业本(1)7.4 (2)基础练习必做，希望完成综合运用.
3、课课练B7.4(2)当堂训练必做, 课后作业选做.1.对于函数y=2x+7, 当x1≤x≤x2, ≤y≤ ；2x1+72x2+72.已知y是关于x的一次 函数，这个函数的图象经过 A（0，-8），B（1，2）两点，求当1（1）它的图象是经过点（－1，2）的一条直线；（2）函数值随自变量的增大而增大；请写出符合上述条件的一个函数解析式：___________拓展提高 7. 某段公路上依次有A、B、C三个车站（如图）。上午8时，甲骑自行车从A、B间离A站18千米的P处出发，向C站匀速前进，经过15分到达离A站22千米处。已知A、B间和B、C间的距离分别是30千米和20千米，问在哪个时间段，甲在B、C两站之间(不包括B、C)？拓展提高8、在如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，P为BC边上一点（不与B、C重合）,设CP=x， △APB的面积为s。
（1）求s关于x的函数解析式及自变量x的取值范围。（2）画出函数的图象。（3）请说出s与x的变化情况。拓展提高9、你能根据下图编个故事吗？（任选其一）拓展提高谢谢，再见！