3.2三角形内切圆
图片预览

文档简介
课件22张PPT。3.2 三角形的内切圆1、确定圆的条件是什么?1.圆心与半径2、叙述角平线的性质与判定性质:角平线上的点到这个角的两边的距离相等。
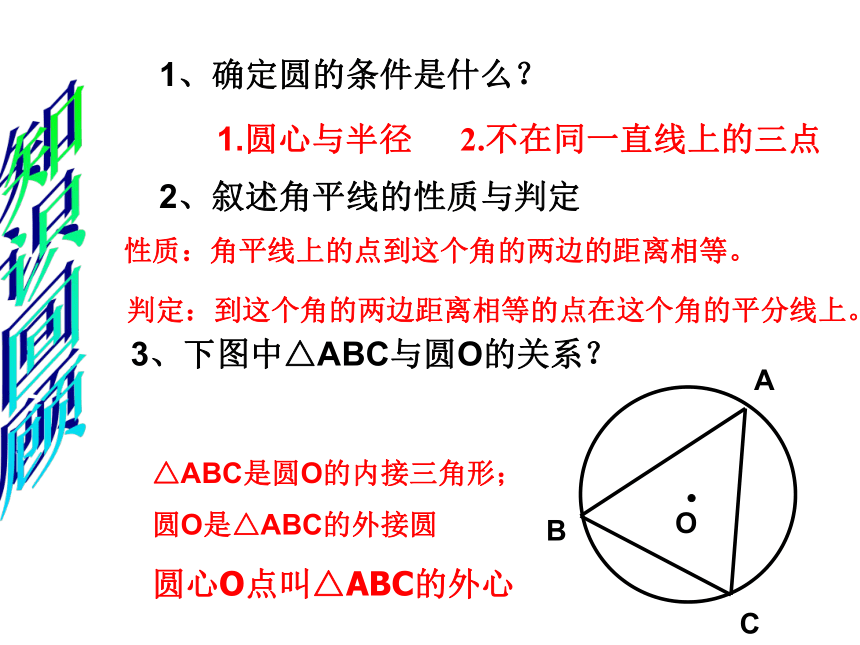
3、下图中△ABC与圆O的关系?△ABC是圆O的内接三角形;
圆O是△ABC的外接圆
圆心O点叫△ABC的外心知识回顾2.不在同一直线上的三点判定:到这个角的两边距离相等的点在这个角的平分线上。 李师傅在一家玻璃厂上班,工作之余想
对厂里的三角形废料(如图)进行加工,裁
下一块半径尽可能大的圆形用料做圆桌的桌
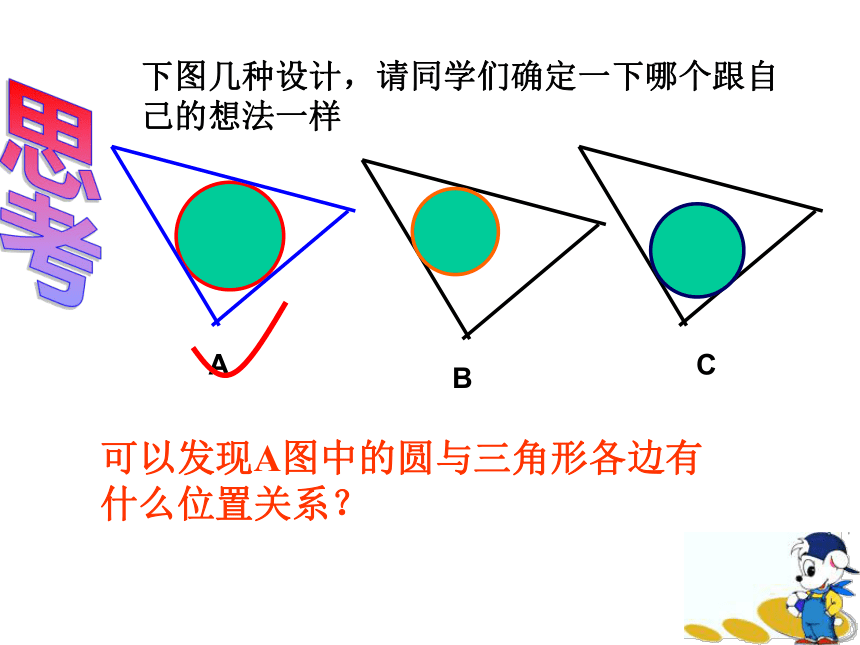
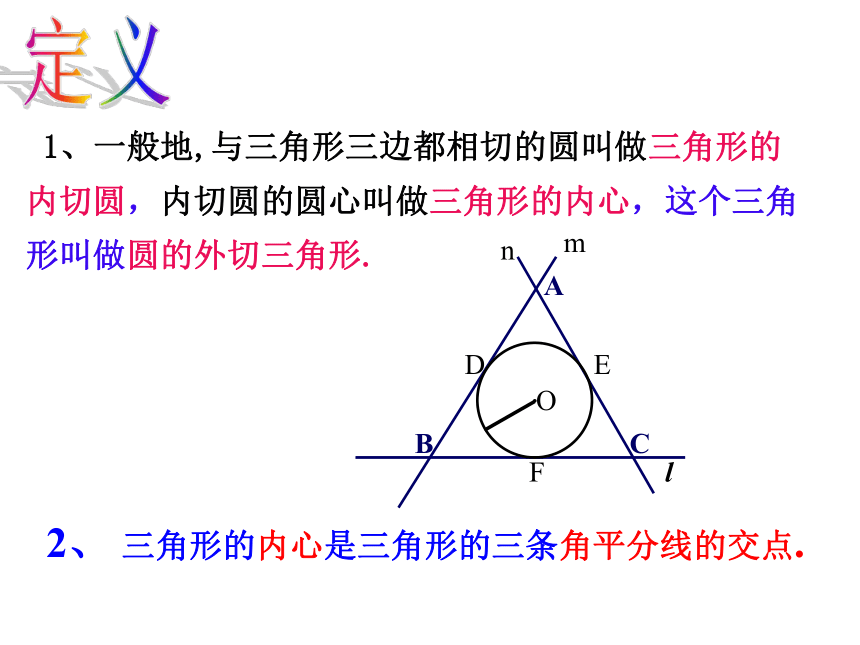
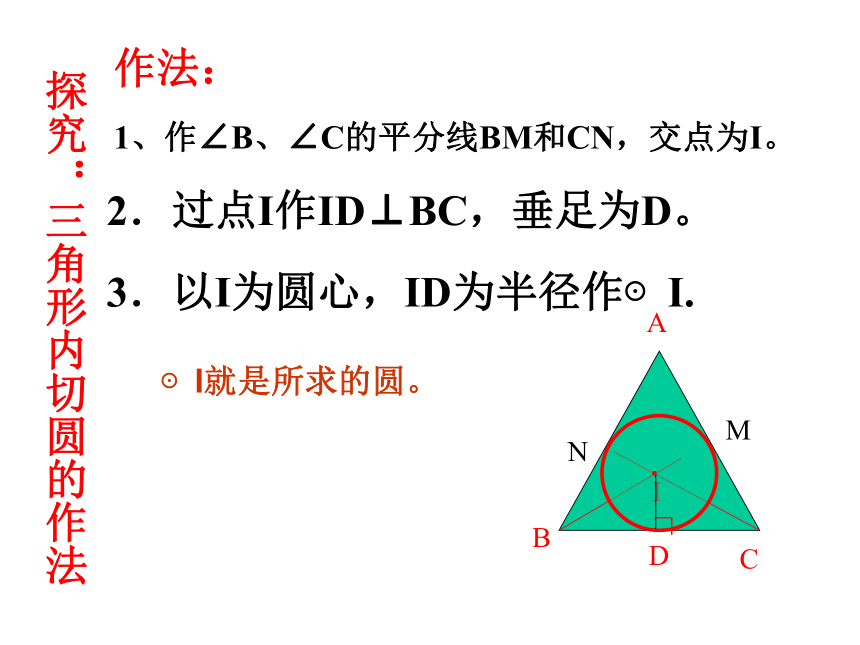
面。你能帮他画出裁剪图吗?下图几种设计,请同学们确定一下哪个跟自己的想法一样思考ABC可以发现A图中的圆与三角形各边有什么位置关系? 1、一般地,与三角形三边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.定义 2、 三角形的内心是三角形的三条角平分线的交点.作法: ABC1、作∠B、∠C的平分线BM和CN,交点为I。 I2.过点I作ID⊥BC,垂足为D。 3.以I为圆心,ID为半径作⊙I. MN探究:三角形内切圆的作法⊙I就是所求的圆。∟.画三角形内切圆的步骤:
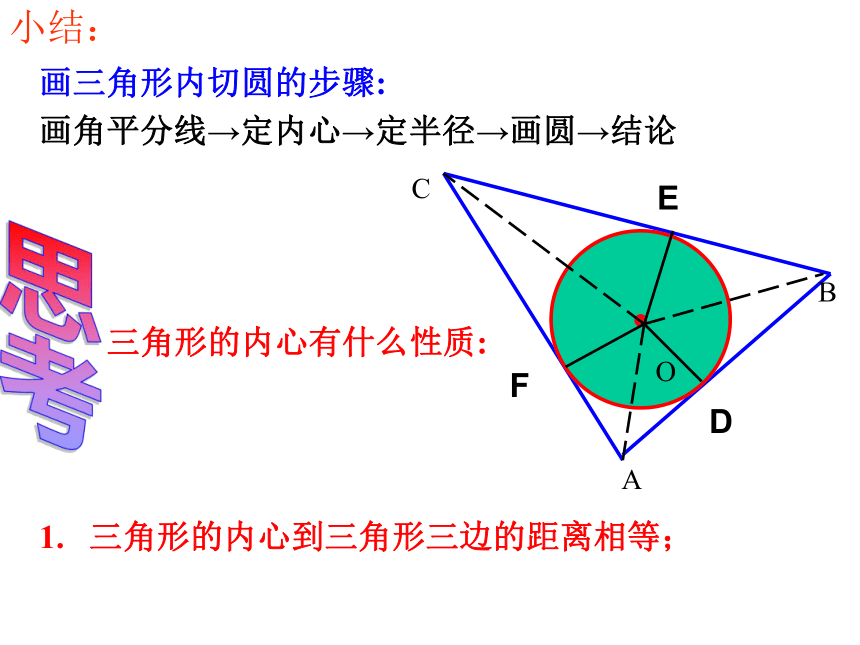
画角平分线→定内心→定半径→画圆→结论OACB小结:1. 三角形的内心到三角形三边的距离相等;三角形的内心有什么性质:思考三角形三边
中垂线的交
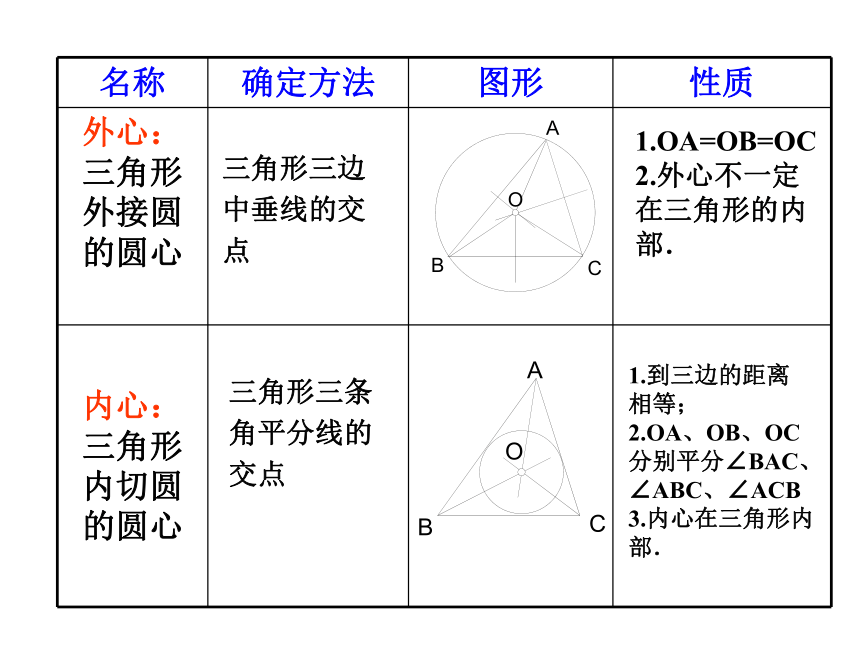
点1.OA=OB=OC
2.外心不一定在三角形的内部.三角形三条
角平分线的
交点1.到三边的距离
相等;
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
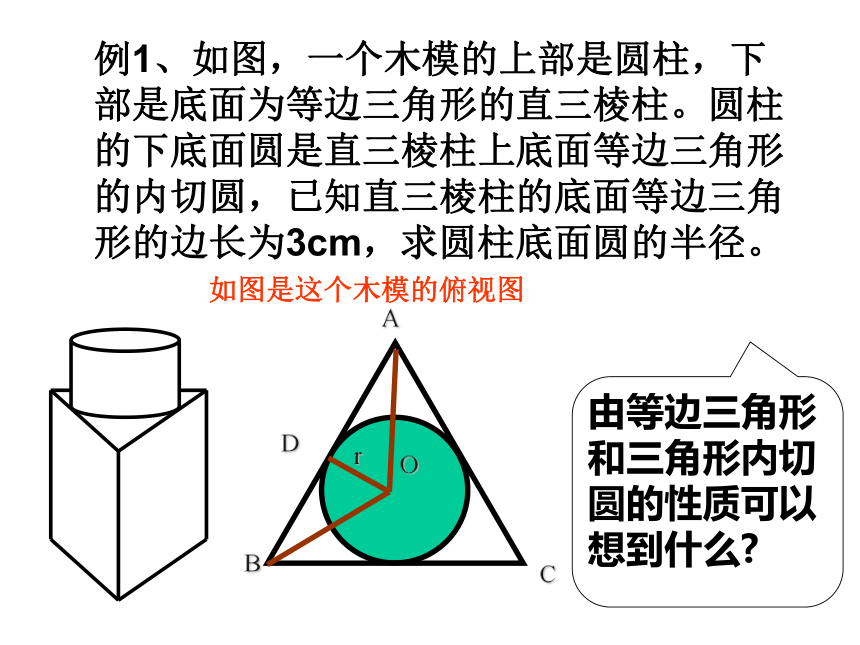
3.内心在三角形内部.例1、如图,一个木模的上部是圆柱,下部是底面为等边三角形的直三棱柱。圆柱的下底面圆是直三棱柱上底面等边三角形的内切圆,已知直三棱柱的底面等边三角形的边长为3cm,求圆柱底面圆的半径。CABrOD由等边三角形和三角形内切圆的性质可以想到什么?如图是这个木模的俯视图CABrOD例1、如图,一个木模的上部是圆柱,下部是底面为等边三角形的直三棱柱。圆柱的下底面圆是直三棱柱上底面等边三角形的内切圆,已知直三棱柱的底面等边三角形的边长为3cm,求圆柱底面圆的半径。解: 如图是这个木模的俯视图,设圆o切AB于点D,连结OA,
OB,OD.∵圆o是△ABC的内切圆,∴AO,BO是∠BAC, ∠ABC的角平分线∵ △ABC是等边三角形,∴ ∠OAB=∠OBA=300∵OD⊥AB,AB=3cm,∴AD=BD= AB=1.5(cm)∴OD=AD. tan300= (cm)答:圆柱底面圆的半径为 cm.练习:已知正三角形的边长为6.求它的内切圆和外接圆的半径。OABCDOD=OA=可见正三角形内切圆和外接圆的半径之比是1:2例2、如图,已知⊙O 是△ABC的内切圆,切点分别点D、E、F,设△ABC周长为L。
求证:AE+BC= LAB·EFOCD证明:连接OE,OF,OA.∵⊙O是△ABC的内切圆,E,F 为切点,∴∠AEO=∠AFO=90°.又∵OE=OF,OA=OA,∴△AOE≌ △AOF.∴ AE=AF同理,BD=BF,CD=CE.∴ AE+BC=AE+BD+CD= (AE+AF+BD+BF+CD+CE)=(HL)已知:在△ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F, 求AF、BD和CE的长。ABCFDExx13-x13-x9-x9-x∴(13-x)+(9-x)=14解得x=4答:AF=4
BD=9
CE=5∴AF=4,BD=9,CE=5
练习:ABCODEr如:直角三角形的两直角边分别是5cm,12cm 则其内切圆的半径为______。 变式拓展1:
如图,直角三角形的两直角边分别是a,b,斜边为c 则其内切圆的半径r为:
(以含a、b、c的代数式表示r)2cmFrr如图.已知△ABC的三边BC,AB,AC分别为
a,b,c,O为内心,内切圆半径为r,
求△ABC的面积(用a,b,c,r表示)证明:连结AO,BO,CO
S△ABC=S△BCO + S△ABO + S△ACO练习:
⑴边长为3,4,5的三角形的内切圆半径是__
⑵边长为5,5,6的三角形的内切圆半径是__11.5变式拓展2:(三)、特殊三角形外接圆、内切圆半径的求法:ABCOIabc直角三角形外接圆、内切圆半径的求法1、定义:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.2、画三角形的内切圆:
画角平分线→定内心→定半径→画圆→结论3、性质:内心到三角形三边的距离相等;
内心与顶点连线平分内角。4、简单应用课堂小结:作业作业:
1、作业本(2) 3.2
2、同步练习与测评:3.2题1: 如图,在△ABC中,点O是内心,∠ABC=50°,∠ACB=70°,求∠BOC的度数。变式1:在△ABC中,点O是内心,
∠BAC=50°,求∠BOC的度数。变式2:在△ABC中,点O是内心,
∠BOC=120°,求∠BAC的度数。若∠BAC=X °则∠BOC= °115°60°120°(2)若∠A=80 °,则∠BOC = 度。
(3)若∠BOC=100 °,则∠A = 度。解:13020(1)∵点O是△ABC的内心,∴ ∠BOC=180 °-(∠1+ ∠3)= 180 °-(25°+ 35 °)=120 °同理 ∠3= ∠4= ∠ACB= ?70° =35 °∴ ∠1= ∠2= ∠ABC= ?50°= 25°理由: ∵点O是△ABC的内心,∴ ∠1+ ∠3 = (∠ABC+ ∠ACB)∴ ∠1= ∠ABC, ∠3= ∠ACB= 180 °-( 90 ° - ∠A )= (180 ° - ∠A )= 90 °+ ∠A= 90 ° - ∠A答: ∠BOC =90 ° + ∠A(4)试探索: ∠A与∠BOC之间存在怎样的数量关系?请说明理由。在△OBC中,∠BOC =180 °-( ∠1+ ∠3 )如图,I是?ABC的内心,连结AI并延长交BC边于点D,交?ABC的外接圆于点E. 求证:(1) EI = EB ;(2)IE 2 = AE · DE .分析拓展提高题:
3、下图中△ABC与圆O的关系?△ABC是圆O的内接三角形;
圆O是△ABC的外接圆
圆心O点叫△ABC的外心知识回顾2.不在同一直线上的三点判定:到这个角的两边距离相等的点在这个角的平分线上。 李师傅在一家玻璃厂上班,工作之余想
对厂里的三角形废料(如图)进行加工,裁
下一块半径尽可能大的圆形用料做圆桌的桌
面。你能帮他画出裁剪图吗?下图几种设计,请同学们确定一下哪个跟自己的想法一样思考ABC可以发现A图中的圆与三角形各边有什么位置关系? 1、一般地,与三角形三边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.定义 2、 三角形的内心是三角形的三条角平分线的交点.作法: ABC1、作∠B、∠C的平分线BM和CN,交点为I。 I2.过点I作ID⊥BC,垂足为D。 3.以I为圆心,ID为半径作⊙I. MN探究:三角形内切圆的作法⊙I就是所求的圆。∟.画三角形内切圆的步骤:
画角平分线→定内心→定半径→画圆→结论OACB小结:1. 三角形的内心到三角形三边的距离相等;三角形的内心有什么性质:思考三角形三边
中垂线的交
点1.OA=OB=OC
2.外心不一定在三角形的内部.三角形三条
角平分线的
交点1.到三边的距离
相等;
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
3.内心在三角形内部.例1、如图,一个木模的上部是圆柱,下部是底面为等边三角形的直三棱柱。圆柱的下底面圆是直三棱柱上底面等边三角形的内切圆,已知直三棱柱的底面等边三角形的边长为3cm,求圆柱底面圆的半径。CABrOD由等边三角形和三角形内切圆的性质可以想到什么?如图是这个木模的俯视图CABrOD例1、如图,一个木模的上部是圆柱,下部是底面为等边三角形的直三棱柱。圆柱的下底面圆是直三棱柱上底面等边三角形的内切圆,已知直三棱柱的底面等边三角形的边长为3cm,求圆柱底面圆的半径。解: 如图是这个木模的俯视图,设圆o切AB于点D,连结OA,
OB,OD.∵圆o是△ABC的内切圆,∴AO,BO是∠BAC, ∠ABC的角平分线∵ △ABC是等边三角形,∴ ∠OAB=∠OBA=300∵OD⊥AB,AB=3cm,∴AD=BD= AB=1.5(cm)∴OD=AD. tan300= (cm)答:圆柱底面圆的半径为 cm.练习:已知正三角形的边长为6.求它的内切圆和外接圆的半径。OABCDOD=OA=可见正三角形内切圆和外接圆的半径之比是1:2例2、如图,已知⊙O 是△ABC的内切圆,切点分别点D、E、F,设△ABC周长为L。
求证:AE+BC= LAB·EFOCD证明:连接OE,OF,OA.∵⊙O是△ABC的内切圆,E,F 为切点,∴∠AEO=∠AFO=90°.又∵OE=OF,OA=OA,∴△AOE≌ △AOF.∴ AE=AF同理,BD=BF,CD=CE.∴ AE+BC=AE+BD+CD= (AE+AF+BD+BF+CD+CE)=(HL)已知:在△ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F, 求AF、BD和CE的长。ABCFDExx13-x13-x9-x9-x∴(13-x)+(9-x)=14解得x=4答:AF=4
BD=9
CE=5∴AF=4,BD=9,CE=5
练习:ABCODEr如:直角三角形的两直角边分别是5cm,12cm 则其内切圆的半径为______。 变式拓展1:
如图,直角三角形的两直角边分别是a,b,斜边为c 则其内切圆的半径r为:
(以含a、b、c的代数式表示r)2cmFrr如图.已知△ABC的三边BC,AB,AC分别为
a,b,c,O为内心,内切圆半径为r,
求△ABC的面积(用a,b,c,r表示)证明:连结AO,BO,CO
S△ABC=S△BCO + S△ABO + S△ACO练习:
⑴边长为3,4,5的三角形的内切圆半径是__
⑵边长为5,5,6的三角形的内切圆半径是__11.5变式拓展2:(三)、特殊三角形外接圆、内切圆半径的求法:ABCOIabc直角三角形外接圆、内切圆半径的求法1、定义:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.2、画三角形的内切圆:
画角平分线→定内心→定半径→画圆→结论3、性质:内心到三角形三边的距离相等;
内心与顶点连线平分内角。4、简单应用课堂小结:作业作业:
1、作业本(2) 3.2
2、同步练习与测评:3.2题1: 如图,在△ABC中,点O是内心,∠ABC=50°,∠ACB=70°,求∠BOC的度数。变式1:在△ABC中,点O是内心,
∠BAC=50°,求∠BOC的度数。变式2:在△ABC中,点O是内心,
∠BOC=120°,求∠BAC的度数。若∠BAC=X °则∠BOC= °115°60°120°(2)若∠A=80 °,则∠BOC = 度。
(3)若∠BOC=100 °,则∠A = 度。解:13020(1)∵点O是△ABC的内心,∴ ∠BOC=180 °-(∠1+ ∠3)= 180 °-(25°+ 35 °)=120 °同理 ∠3= ∠4= ∠ACB= ?70° =35 °∴ ∠1= ∠2= ∠ABC= ?50°= 25°理由: ∵点O是△ABC的内心,∴ ∠1+ ∠3 = (∠ABC+ ∠ACB)∴ ∠1= ∠ABC, ∠3= ∠ACB= 180 °-( 90 ° - ∠A )= (180 ° - ∠A )= 90 °+ ∠A= 90 ° - ∠A答: ∠BOC =90 ° + ∠A(4)试探索: ∠A与∠BOC之间存在怎样的数量关系?请说明理由。在△OBC中,∠BOC =180 °-( ∠1+ ∠3 )如图,I是?ABC的内心,连结AI并延长交BC边于点D,交?ABC的外接圆于点E. 求证:(1) EI = EB ;(2)IE 2 = AE · DE .分析拓展提高题:
