2.22二次函数的图象

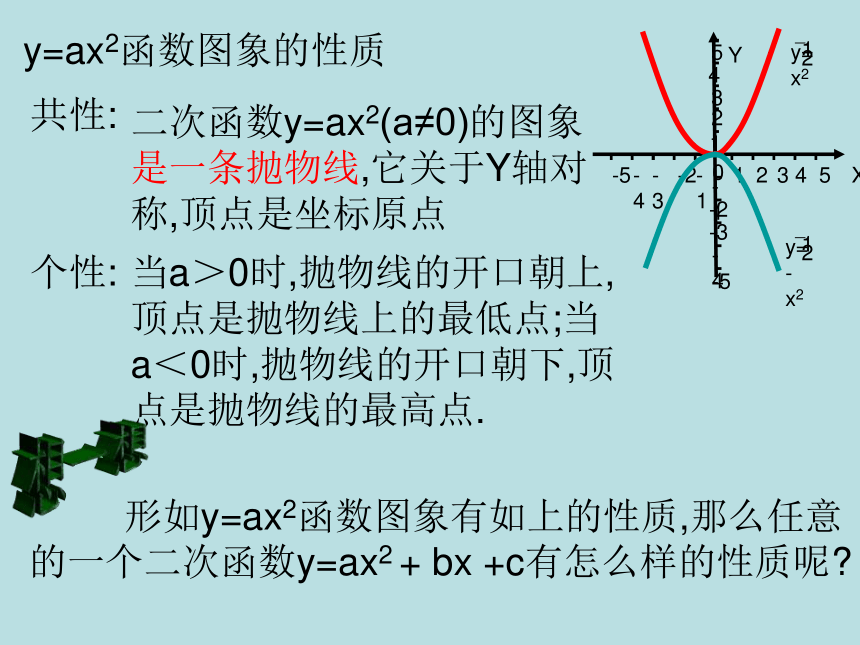
课件18张PPT。二次函数的图象和性质y=x2y= x2y= x2 +2xy= x2 +2x+2y=ax2（简单）y=ax2 +bx+c（复杂）画函数图象的三步骤①列表 ②描点 ③连线①列表00.524.50.524.5②描点y= x2②描点③连线y=ax2函数图象的性质共性:个性:二次函数y=ax2(a≠0)的图象是一条抛物线,它关于Y轴对称,顶点是坐标原点当a＞0时,抛物线的开口朝上,顶点是抛物线上的最低点;当a＜0时,抛物线的开口朝下,顶点是抛物线的最高点. 形如y=ax2函数图象有如上的性质,那么任意
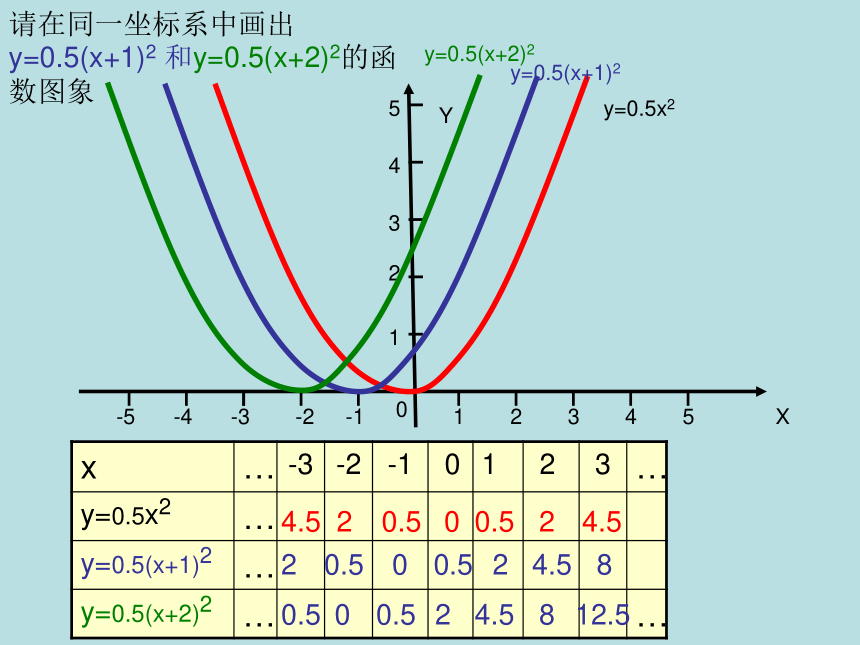
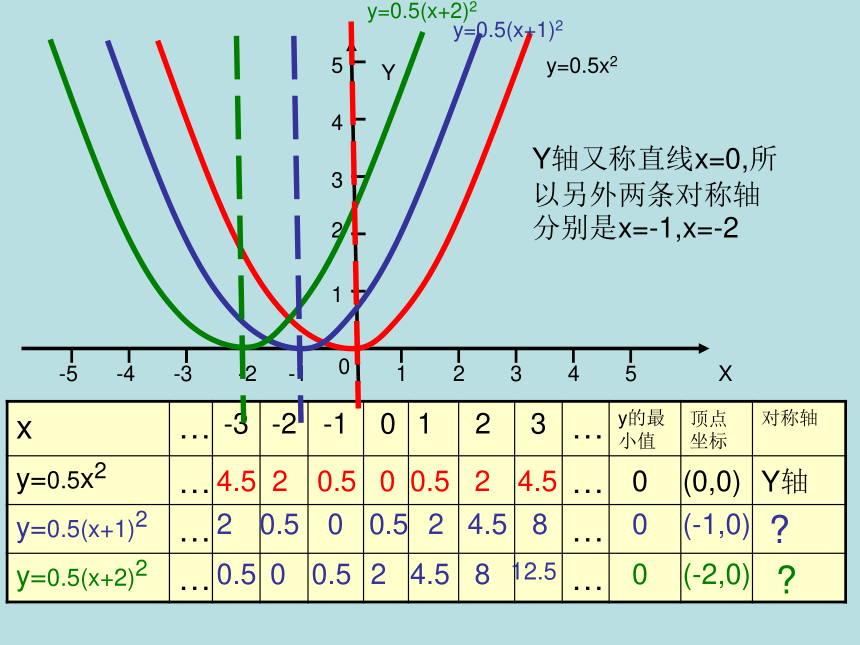
的一个二次函数y=ax2 + bx +c有怎么样的性质呢?想一想XY123450-1-2-3-4-512345y=0.5x20.54.52800.520.50.54.528012.5y=0.5(x+1)2y=0.5(x+2)2请在同一坐标系中画出y=0.5(x+1)2 和y=0.5(x+2)2的函数图象XY123450-1-2-3-4-512345y=0.5x20.54.52800.520.50.54.528012.5y=0.5(x+1)2y=0.5(x+2)2000(0,0)(-1,0)(-2,0)Y轴??Y轴又称直线x=0,所以另外两条对称轴分别是x=-1,x=-2XY123450-1-2-3-4-512345y=0.5x2y=0.5(x+1)2y=0.5(x+2)21,它们有什么共同特征?2,顶点坐标和对称轴有什么关系?3,图象之间的位置能否通过适当变换得到?开口朝上,形状相同000(0,0)(-1,0)(-2,0)Y轴（直线x=0）直线x=-1直线x=-24,你能得到y=0.5(x+3)2 ，y=0.5(x-3)2的图像吗？总结: 一般地,函数y=a(x+m)2(a≠0)的图象与函数y=ax2的图象只是位置不同,它可由y=ax2的图象向右(当m＜0时)或向左(当m＞0时)平移|m|个单位得到, 函数y=a(x+m)2的顶点坐标是(-m,0),对称轴是直线x=-m,顶点在图象上的位置特征、图象的开口方向与函数y=ax2的图象相同。平移法则：左加右减y=x2y=(x+3)2经过怎样的平移可得y=(x- )2y=3(x+1)2y=3x2 二次函数的二次项系数必须相同时，才可以互相平移！注意平移法则：左加右减例.用描点法在同一直角坐标系中画出函数活动二:活动后要求:说说它们有什么共同特征? 图象之间的位置能否通过适当的变换得到?由此, 你有什么发现?说说你的想法!3.53.57.55357.5XY123450-1-2-3-4-512345y=0.5(x+2)2y=0.5(x+2)2+3XY123450-1-2-3-4-512345y=0.5(x+2)2y=0.5(x+2)2+330(-2,3)(-2,0)直线x=-2直线x=-2直线x=-2经历了怎样的图形变化？上加下减从图象可知:把函数 的图象向上平移3个单位,就得到函数 的图象.因此,只要将函数 的图象先向左平移2个单位,再向上平移3个单位,就得到函数 的图象.归纳: 一般地,函数y=a(x+m)2+k(a≠0)的图象,可以由函数y=ax2的图象
先向右(当m＜0)或向左(当m＞0)平移|m|个单位,
再向上(当k＞0)或向下(当k＜0)平移|k|个单位得到,
顶点是(-m,k)
对称轴是直线 x=-m,
顶点在图象的位置特征和图象
的开口方向与函数y=ax2的图象相同.课内练习书本34页，1，2题思考题 请任意写一个二次函数，说出它的图形变换过程例如：y=3x2+6x+7解：y=3(x2+2x)+7 配方得：y=3(x2+2x+1- 1)+7y=3(x+1)2- 3+7y=3(x+1)2+4y=3x2经过怎么样的变换可以得到y=3(x+1)2+4？y=a(x+m)2+k和y=ax2+bx+c（a≠0 ）的关系二次函数的配方式二次函数的一般式