3.42圆周角
图片预览



文档简介
课件19张PPT。3.4圆周角 (2)特征:① 角的顶点在圆上.② 角的两边都与圆相交.1、圆周角定义: 顶点在圆上,
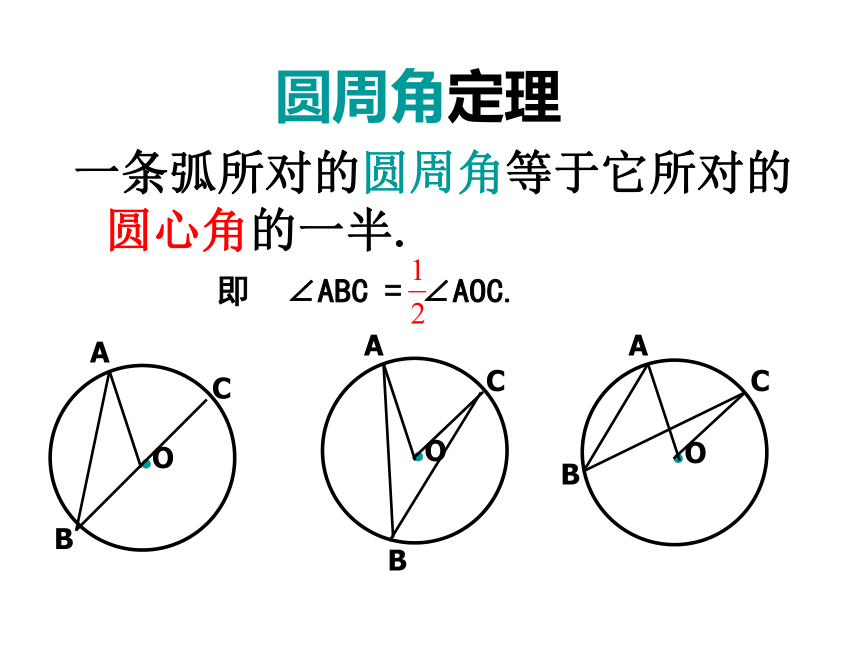
并且两边都和圆相交的角叫圆周角.4A一、旧知回放:2、圆心角与所对的弧的关系3、圆周角与所对的弧的关系4、同弧所对的圆心角与圆周角的关系一、旧知回放:圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半.即 ∠ABC = ∠AOC.1、100o的弧所对的圆心角等于_______,所对的圆周角等于_______。
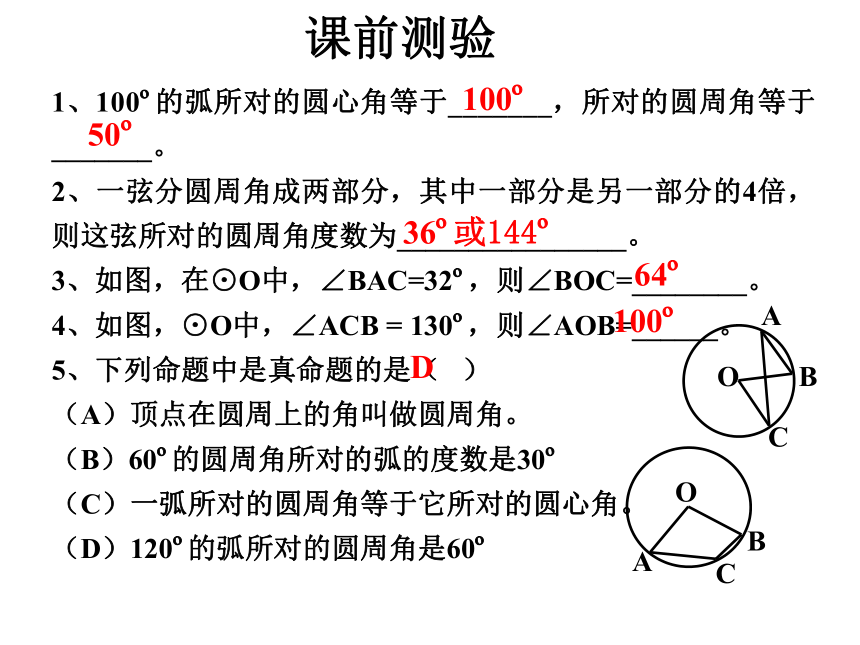
2、一弦分圆周角成两部分,其中一部分是另一部分的4倍,则这弦所对的圆周角度数为________________。
3、如图,在⊙O中,∠BAC=32o,则∠BOC=________。
4、如图,⊙O中,∠ACB = 130o,则∠AOB=______。
5、下列命题中是真命题的是( )
(A)顶点在圆周上的角叫做圆周角。
(B)60o的圆周角所对的弧的度数是30o
(C)一弧所对的圆周角等于它所对的圆心角。
(D)120o的弧所对的圆周角是60o课前测验B
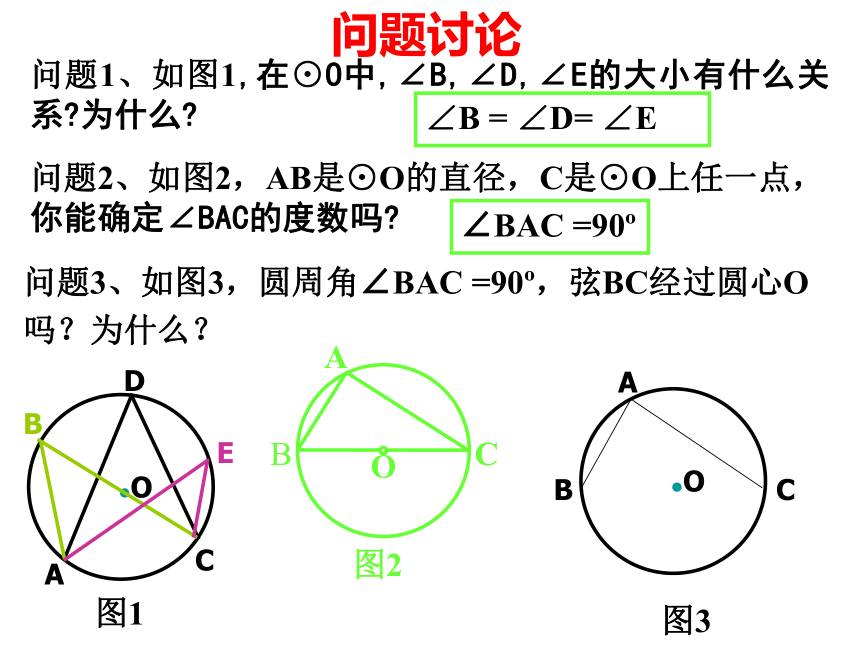
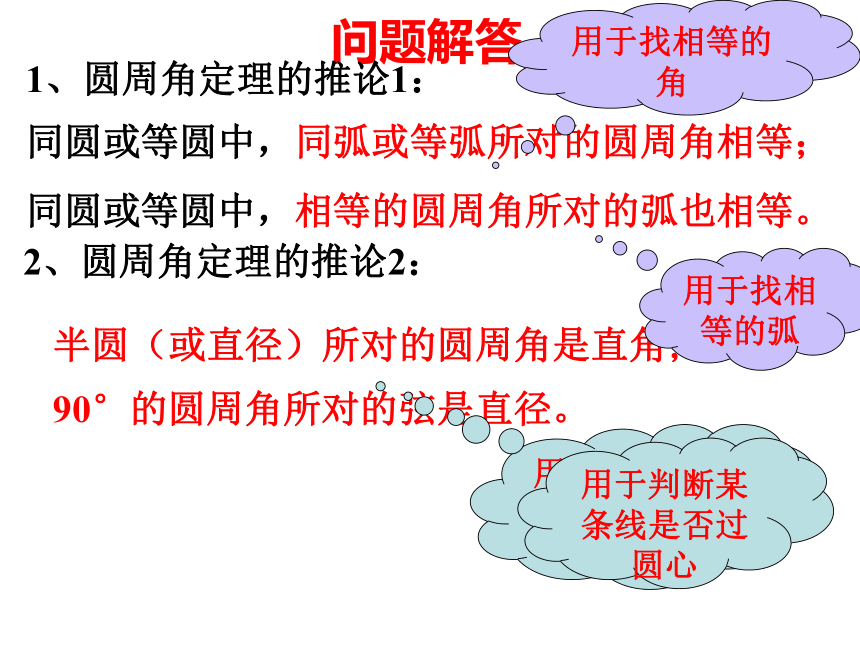
100o50o36o或144o64o100oD问题讨论问题1、如图1,在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?图1问题3、如图3,圆周角∠BAC =90o,弦BC经过圆心O吗?为什么?∠B = ∠D= ∠E∠BAC =90o问题解答1、圆周角定理的推论1:同圆或等圆中,同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。2、圆周角定理的推论2:半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径。用于找相等的角用于找相等的弧用于判断某个圆周角是否是直角用于判断某条线是否过圆心例2已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
求证:⌒ ⌒BD=DE证明:连结AD.∵AB是圆的直径,点D在圆上,∴∠ADB=90°,∴AD⊥BC,∵AB=AC,∴AD平分顶角∠BAC,即∠BAD=∠CAD,∴ ⌒ ⌒BD= DE(同圆或等圆中,相等的圆周角所对弧相等)。练习:如图,P是△ABC的外接圆上的一点∠APC=∠CPB=60°。求证:△ABC是等边三角形证明:∵∠ABC和∠APC
都是⌒所对的圆周角。 AC∴∠ABC=∠APC=60°(同弧所对的圆周角相等)同理,∵∠BAC和∠CPB都是⌒所对的圆周角,BC∴∠BAC=∠CPB=60°。∴△ABC等边三角形。例3: 船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁。如图A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点,∠ACB就是“危险角”,当船与两个灯塔的夹角大于“危险角”时,就有可能触礁。弓形所含的圆周角∠C=50°,问船在航行时怎样才能保证不进入暗礁区?(1)当船与两个灯塔的夹角∠α大于“危险角”时,船位于哪个区域?为什么?(2)当船与两个灯塔的夹角∠α小于“危险角”时,船位于哪个区域?为什么?例4:一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.ABC例4:一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.ABCD练一练:1.说出命题’圆的两条平行弦所夹的弧相等”的逆命题.原命题和逆命题都是真命题吗?请说明理由.2.已知:四边形ABCD内接于圆,BD平分∠ABC,且AB∥CD.求证:AB=CD想一想:如图:AB是⊙O的直径,弦CD⊥AB于点E,G是⌒上任意一点,延长AG,与DC的延长线相交于点F,连接AD,GD,CG,找出图中所有和∠ADC相等的角,并说明理由.AC1如图,⊙O中,AB是直径,半径CO⊥AB,D是CO的中点,DE // AB,求证:EC=2EA.提高拓展:⌒⌒2,已知BC为半圆O的直径,AB=AF,AC交BF于点M,过A点作AD⊥BC于D,交BF于E,则AE与BE的大小有什么关系?为什么?1、本节课我们学习了哪些知识?
2、圆周角定理及其推论的用途你都知道了吗?
谈谈你的收获、感受!再见
并且两边都和圆相交的角叫圆周角.4A一、旧知回放:2、圆心角与所对的弧的关系3、圆周角与所对的弧的关系4、同弧所对的圆心角与圆周角的关系一、旧知回放:圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半.即 ∠ABC = ∠AOC.1、100o的弧所对的圆心角等于_______,所对的圆周角等于_______。
2、一弦分圆周角成两部分,其中一部分是另一部分的4倍,则这弦所对的圆周角度数为________________。
3、如图,在⊙O中,∠BAC=32o,则∠BOC=________。
4、如图,⊙O中,∠ACB = 130o,则∠AOB=______。
5、下列命题中是真命题的是( )
(A)顶点在圆周上的角叫做圆周角。
(B)60o的圆周角所对的弧的度数是30o
(C)一弧所对的圆周角等于它所对的圆心角。
(D)120o的弧所对的圆周角是60o课前测验B
100o50o36o或144o64o100oD问题讨论问题1、如图1,在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?图1问题3、如图3,圆周角∠BAC =90o,弦BC经过圆心O吗?为什么?∠B = ∠D= ∠E∠BAC =90o问题解答1、圆周角定理的推论1:同圆或等圆中,同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。2、圆周角定理的推论2:半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径。用于找相等的角用于找相等的弧用于判断某个圆周角是否是直角用于判断某条线是否过圆心例2已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
求证:⌒ ⌒BD=DE证明:连结AD.∵AB是圆的直径,点D在圆上,∴∠ADB=90°,∴AD⊥BC,∵AB=AC,∴AD平分顶角∠BAC,即∠BAD=∠CAD,∴ ⌒ ⌒BD= DE(同圆或等圆中,相等的圆周角所对弧相等)。练习:如图,P是△ABC的外接圆上的一点∠APC=∠CPB=60°。求证:△ABC是等边三角形证明:∵∠ABC和∠APC
都是⌒所对的圆周角。 AC∴∠ABC=∠APC=60°(同弧所对的圆周角相等)同理,∵∠BAC和∠CPB都是⌒所对的圆周角,BC∴∠BAC=∠CPB=60°。∴△ABC等边三角形。例3: 船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁。如图A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点,∠ACB就是“危险角”,当船与两个灯塔的夹角大于“危险角”时,就有可能触礁。弓形所含的圆周角∠C=50°,问船在航行时怎样才能保证不进入暗礁区?(1)当船与两个灯塔的夹角∠α大于“危险角”时,船位于哪个区域?为什么?(2)当船与两个灯塔的夹角∠α小于“危险角”时,船位于哪个区域?为什么?例4:一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.ABC例4:一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.ABCD练一练:1.说出命题’圆的两条平行弦所夹的弧相等”的逆命题.原命题和逆命题都是真命题吗?请说明理由.2.已知:四边形ABCD内接于圆,BD平分∠ABC,且AB∥CD.求证:AB=CD想一想:如图:AB是⊙O的直径,弦CD⊥AB于点E,G是⌒上任意一点,延长AG,与DC的延长线相交于点F,连接AD,GD,CG,找出图中所有和∠ADC相等的角,并说明理由.AC1如图,⊙O中,AB是直径,半径CO⊥AB,D是CO的中点,DE // AB,求证:EC=2EA.提高拓展:⌒⌒2,已知BC为半圆O的直径,AB=AF,AC交BF于点M,过A点作AD⊥BC于D,交BF于E,则AE与BE的大小有什么关系?为什么?1、本节课我们学习了哪些知识?
2、圆周角定理及其推论的用途你都知道了吗?
谈谈你的收获、感受!再见
同课章节目录
