4.12 比例线段

课件15张PPT。义务教育课程标准实验教科书4.1比例线段(2)下列四个数是否成比例，如果能，请写出比例式，并指出比例内项、外项。(1) 5 ，3，6，10 (2) 2，0.5，3，12 (3) 7 ，3，4，8 (4) 2.4，0.8，3.2，0.6图片上，表示树高的线段AB长4cm，表示一人高的线段CD长1cm.已知此人高1.6m，则大树的实际高度是多少？你是怎么知道的？3注意：
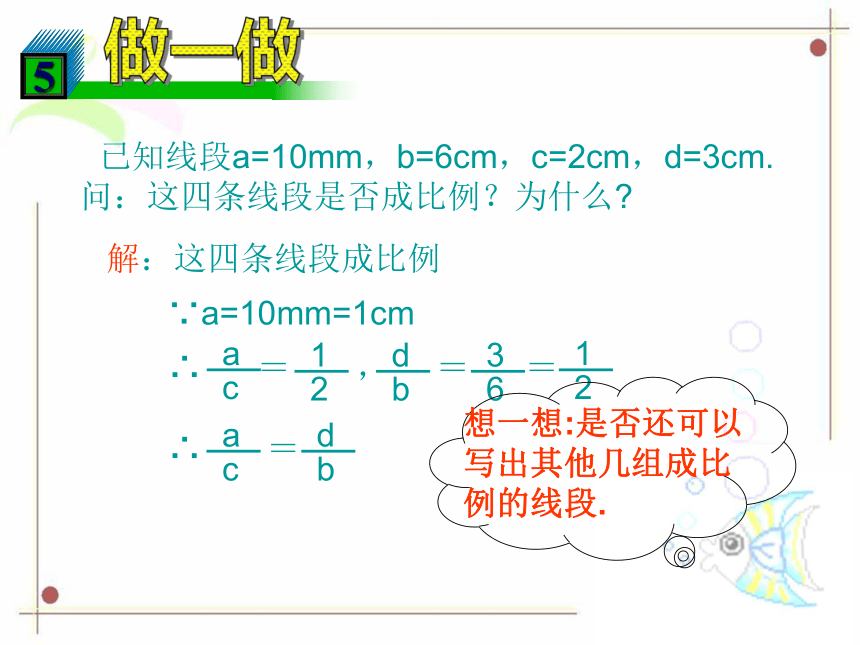
(1)两线段是几何图形，可用它的长度比来确定；(2)度量线段的长，单位多种，但求比值必需在同一长度单位下比值一定是正数，比值与采用的长度单位无关。(3)表示方式与数字的比表示类同，但它也可以表示为AB:CD.定义： 已知线段a=10mm，b=6cm，c=2cm，d=3cm.问：这四条线段是否成比例？为什么?解：这四条线段成比例∵a=10mm=1cm判断四条线段是否成比例的方法有两种： (1)把四条线段按大小排列好，判断前两条线段的比和后两条线段的比是否相等。(2)查看是否有两条线段的积等于其余两条线段的积 。如图，在Rt△ABC中，CD是斜边AB上的高。请找出一组比例线段，并说明理由。分析：(1)根据比例基本性质，要判断四条线段是否成比例，只要采取什么方法(看其中两条线段的乘积是否等于另两条线段的乘积)(2)已知条件中有三角形的高，我们通常可以把高与什么知识联系起来？(3)根据三角形的面积公式，你能得到一个怎样的等式？根据所得的等式可以写出怎样的比例式。 如图，是我国台湾省的几个城市的位置图，问基隆市在高雄市的哪一个方向？到高雄市的实际距离是多少km？(比例尺1：9000000)注意：求角度时要注意方位。解：从图上量出高雄市到基隆市的距离约35mm,设实际距离为s，则∴S＝35×9000000=315000000(mm)即s＝315(km) 量得图中∠ɑ=280,我们还能确定基隆市在高雄市的北偏东280的315km处。答：略2.已知a、b、c、d是比例线段，其中a＝6cm，
b＝8cm，c＝24cm,则线段d的长度是多少？3.已知三角形三条边之比为a：b：c=2：3：4，三角形的周长为18cm，求各边的长。4.已知AB两地的实际距离是60km，画在图上的距离A1B1是6cm，求这幅图的比例尺。 5.现在有一棵很高的古树，欲测出它的高度，但又不能爬到树尖上去直接测量，你有什么好的方法吗？拓展：相同时刻的物高与影长成比例。如果一电视塔在地面上影长为180m，同一时刻高为2m的竹竿的影长为3m，那么电视塔的高是多少？6.如图，已知AD，CE是△ABC中BC、AB上的高线，求证：AD：CE=AB：BC7.如图，在Rt△ABC中，CD⊥AB，DE⊥AC,请找出一组比例线段，并说明理由。8.如图，已知,求知识回顾：说说你在这节课中的收获与体会学习永远是件快乐而有趣的事！作业布置：见作业本9.育美中学请张工程师设计学校的矩形花坛的平面图，这个花坛长为20m，宽为12m。
(1)在比例尺为1:100的平面图上，这个矩形花坛的长和宽各是多少？
(2)在平面图上，这个花坛的长和宽的比是多少？
(3)花坛长和宽实际比是多少？
(4)你发现这两个比有什么关系？