2.1二次函数

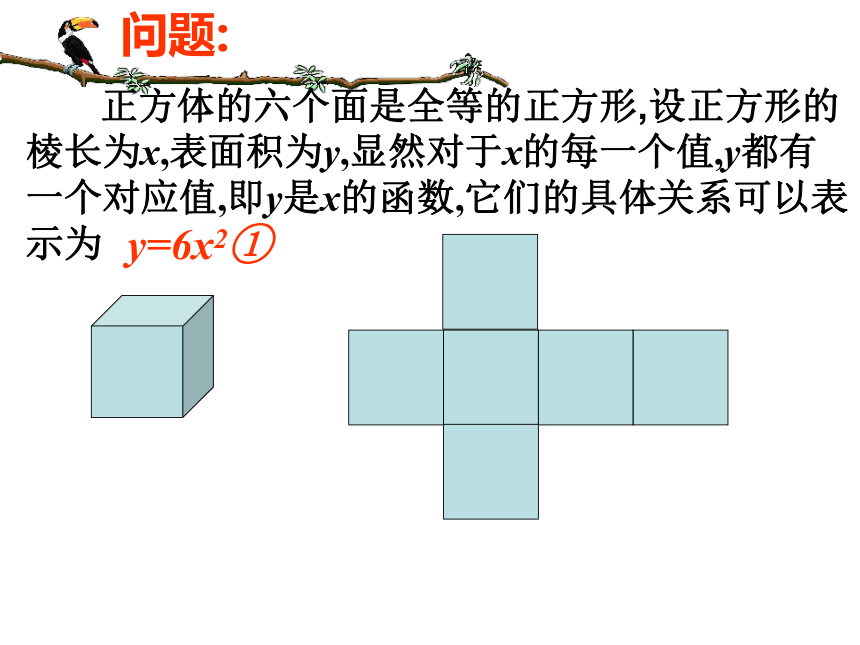
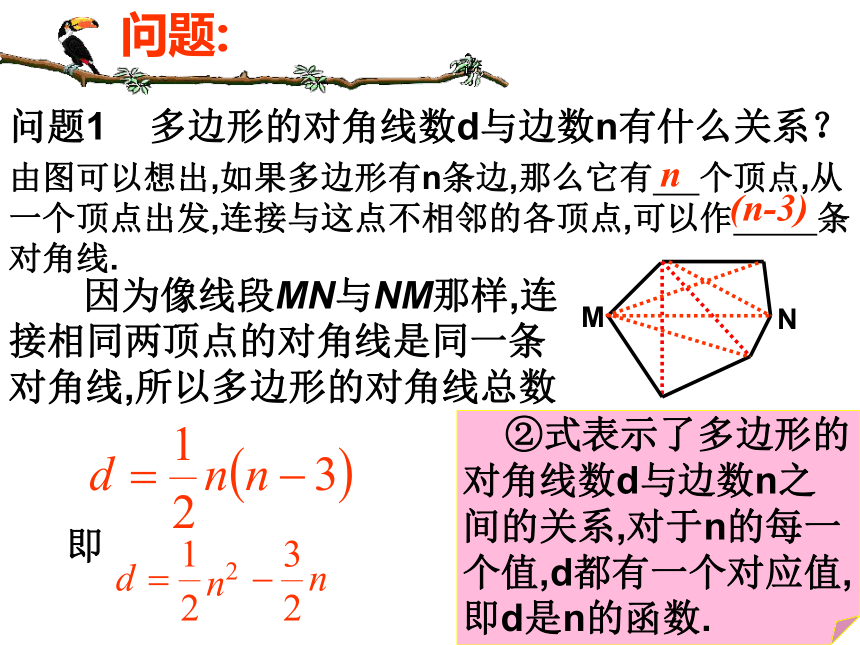
课件16张PPT。 二次函数（1） 正方体的六个面是全等的正方形,设正方形的棱长为x,表面积为y,显然对于x的每一个值,y都有一个对应值,即y是x的函数,它们的具体关系可以表示为 问题:y=6x2①问题1 多边形的对角线数d与边数n有什么关系？问题:由图可以想出,如果多边形有n条边,那么它有 个顶点,从一个顶点出发,连接与这点不相邻的各顶点,可以作 条对角线.n(n-3) 因为像线段MN与NM那样,连接相同两顶点的对角线是同一条对角线,所以多边形的对角线总数
MN即 问题2 某工厂一种产品现在的年产量是20件,计划今后两年增加产量.如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示？问题: 这种产品的原产量是20件, 一年后的产量是
件,再经过一年后的产量是 件,即两年后的产量为
20(1+x)20(1+x)2即 ③式表示了两年后的产量y与计划增产的倍数x之间的关系,对于x的每一个值, y都有一个对应值,即y是x的函数.函数①②③有什么共同点? 观察 y是x的函数吗？y是x的一次函数？反比例函数？y=6x2① 在上面的问题中,函数都是用自变量的二次式表示的,2、定义：一般地，形如y=ax2+bx+c(a,b,c是常数,a≠ 0)的函数叫做x的二次函数。（1）等号左边是变量y，右边是关于自变量x的（3 ）等式的右边最高次数为 ，可以没有一次项和常数项，但不能没有二次项。注意：（2）a,b,c为常数，且（4）x的取值范围是 。整式a≠0.2任意实数二次函数的一般形式:y＝ax2＋bx＋c (其中a、b、c是常数,a≠0)
a是二次项系数b是一次项系数C是常数项二次函数的特殊形式：
当b＝0时， y＝ax2＋c
当c＝0时， y＝ax2＋bx
当b＝0，c＝0时， y＝ax2
例题讲解例1、下列函数中，哪些是二次函数？若是,分别指出二次项系数,一次项系数,常数项.
(1) y=3(x-1)2+1 (2) y=x+
(3) s=3-2t2 (4) y=(x+3)2-x2
(5)y= -x (6) v=10π r2
解:y=3(x-1)2+1
=3(x2-2x+1)+1
=3x2-6x+3+1
即y=3x2-6x+4是二次函数.二次项系数:一次项系数:常数项:3-64不是二次函数.(3) s=3-2t2是二次函数.二次项系数:一次项系数:常数项:-203(4) y=(x+3)2-x2=x2+6x+9-x2
即y=6x+9不是二次函数.二次项系数:一次项系数:常数项:10π00不是二次函数.(6) v=10π r2是二次函数.
一次函数y=ax+b (a ≠0),其中包括正比例函数y=kx(k≠0),
反比例函数y= (k≠0)
二次函数y=ax2+bx+c(a≠0).小结：现在我们学习过的函数有: 可以发现,这些函数的名称都反映了函数表达式与自变量的关系.-1２例题讲解随堂练习2.函数 y=(m-n)x2+ mx+n 是二次函数的条件是( )
A m,n是常数,且m≠0 B m,n是常数,且n≠0
C m,n是常数,且m≠n D m,n为任何实数CC
1.一个圆柱的高等于底面半径,写出它的表面积 s 与半径 r 之间的关系式.
当r为4时s为多少。
2. n支球队参加比赛,每两队之间进行一场比赛,写出比赛的场次数 m与球队数 n 之间的关系式.随堂练习S=4πr2 即3.将进货单价为40元的商品按50元卖出时,就能卖出500个,已知这种商品每涨1元,其销售量就会减少10个,设售价定为X元(x＞50)时的利润为Y元。试求出Y与X的函数关系式，并按所求的函数关系式计算出售定价为80元时所得利润。例4、若二次函数y＝2x2＋bx＋c的图形经过A（－1，0），B（0，1），二点，求这个函数的解析式.例题讲解二次函数 ， 当x=0时，y=-2；当y=-2时，x=0，求y=2时，x的值。 谈谈你的收获小结：