2.2一元二次方程的解法复习

课件14张PPT。一元二次方程的
解法举例 ①因式分解法
②开平方法
③公式法
④配方法
（方程一边是0，另一边整式容易因式分解）（ (x+m)2=a a≥0 ）(化方程为一般式）（二次项系数为1，而一次项系数为偶数）解一元二次方程的方法解:移项,得
方程左边因式分解,得
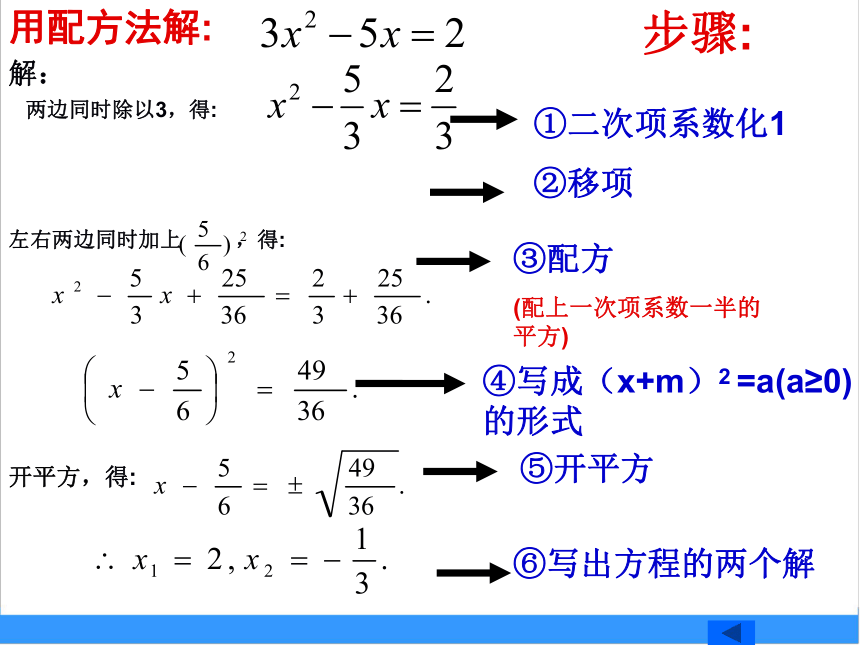
解题步骤:用因式分解法解:用配方法解:解：两边同时除以3，得:左右两边同时加上 ，得:开平方，得:步骤:用公式法解:解:移项,得
这里a=3,b=-5,c=-2=49解题步骤:例1.选择适当的方法解下列方程：①
②
③结论先考虑开平方法,
再用因式分解法;
最后才用公式法和配方法.能不能用整体
思想？例2. 解方程

② 2(x-2)2+5(x-2)-3=0
总结：方程中有括号时，应先用整体思想考虑有没有简单方法，若看不出合适的方法时，则把它去括号并整理为一般形式再选取合理的方法。变1： 2(x-2)2+5(2-x)-3=0再变为： 2(x-2)2+5x-13=02(x-2)2+5x-10-3=0变2： 2(2-x)2+5(2-x)-3=0① (2m+3)2=2(4m+7)(3) (a2+b2)2- (a2+b2)-6=0比一比谁最快：① (y+ )(y- )=2(2y-3)
② 3t(t+2)=2(t+2)
③ x2=4 x-11
④ (x+101)2-10(x+101)+9=0
y1=y2=2
t1=-2,t2=2/3
x1= , x2=
x1=-92,x2=-100
能力拓展解关于x的方程：①②2、 说明无论m取什么实数，方程 x2+(m+1)x－m2-4=0有两个不相等的实数根．３、关于x的一元二次方程x2-mx-5=0。 当m 满足什么条件时，方程的两根为互为相反数？1、 m取什么值时，方程 x2+(2m+1)x+m2-4=0有两个相等的实数解４、已知关于x的方程x2＋３x＋m=0的一个根为x=√２，求另一个根及m的值．(2种方法）小结：ax2+c=0 ====>ax2+bx=0 ====>ax2+bx+c=0 ====>因式分解法公式法（配方法）2、公式法虽然是万能的，对任何一元二次方程都适用，但不一定 是最简单的，因此在解方程时我们首先考虑能否应用“直接开平方法”、“因式分解法”等简单方法，若不行，再考虑公式法（适当也可考虑配方法）3、方程中有括号时，应先用整体思想考虑有没有简单方法，若看不出合适的方法时，则把它去括号并整理为一般形式再选取合理的方法。1、直接开平方法因式分解法