相似三角形的复习(4.2-4.4)
图片预览


文档简介
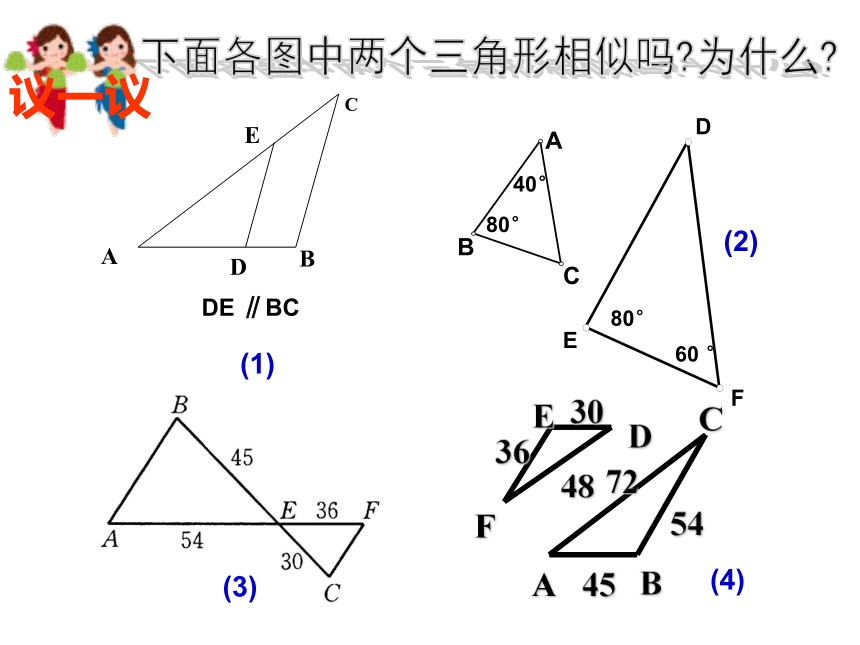
课件24张PPT。相似三角形的复习(4.2-4.4)下面各图中两个三角形相似吗?为什么?DE ∥BC
(1)40°80°60 °80°
(2)
(3)
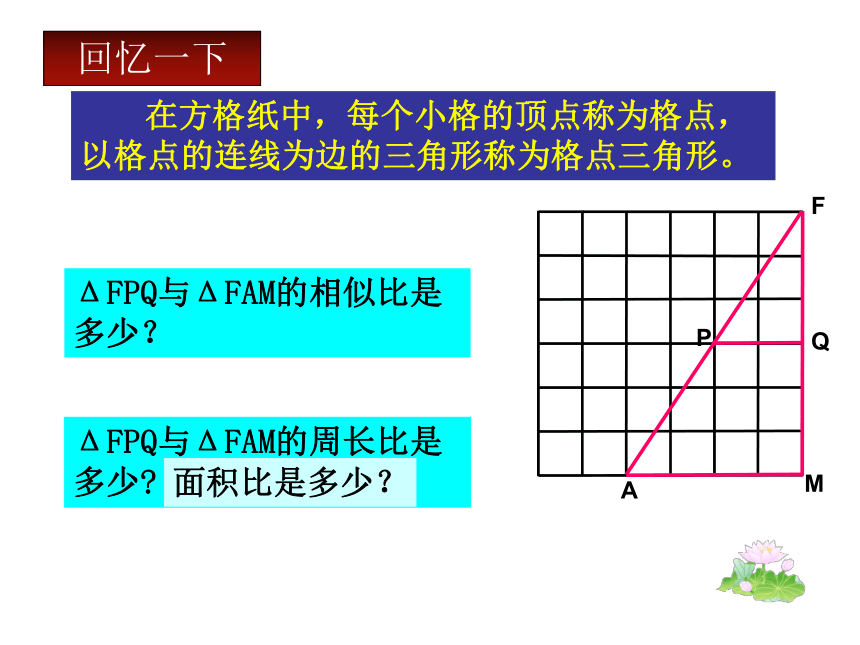
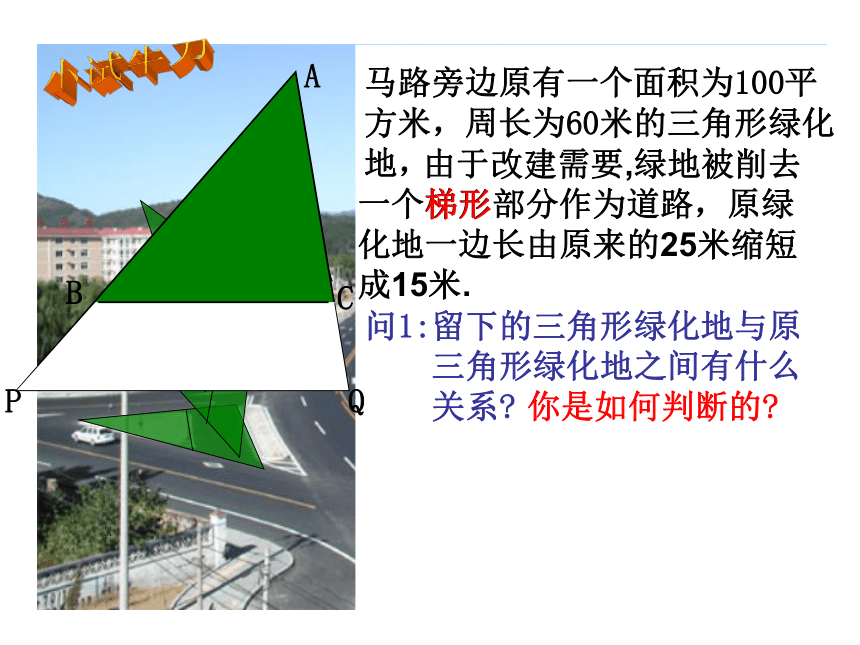
(4)ΔFPQ与ΔFAM的相似比是多少?ΔFPQ与ΔFAM的周长比是多少? 在方格纸中,每个小格的顶点称为格点,以格点的连线为边的三角形称为格点三角形。回忆一下面积比是多少?马路旁边原有一个面积为100平方米,周长为60米的三角形绿化地,
由于改建需要,绿地被削去一个梯形部分作为道路,原绿化地一边长由原来的25米缩短成15米.问1:留下的三角形绿化地与原
三角形绿化地之间有什么
关系?你是如何判断的?梯形小试牛刀 由于改建需要,绿地被削去一个梯形部分作为道路,原绿化地一边长由原来的25米缩短成15米.问1:留下的三角形绿化地与原
三角形绿化地之间有什么
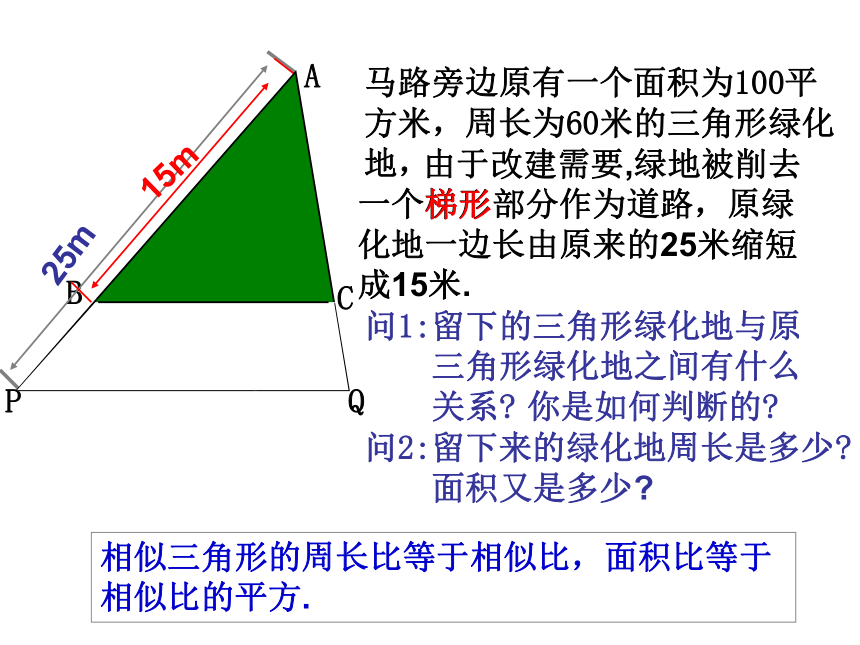
关系?马路旁边原有一个面积为100平方米,周长为60米的三角形绿化地,
问2:留下来的绿化地周长是多少?
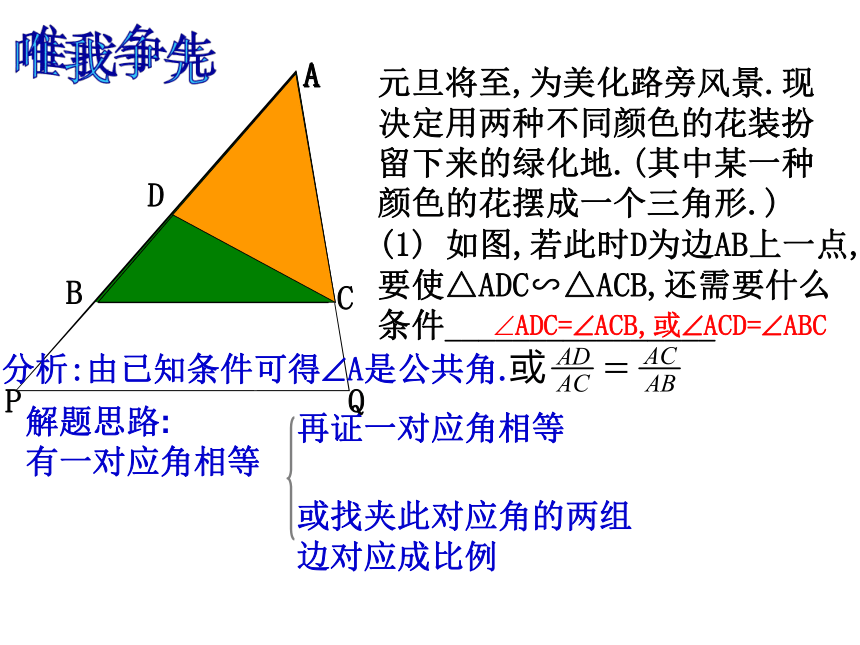
面积又是多少?你是如何判断的?25m15m相似三角形的周长比等于相似比,面积比等于相似比的平方. 梯形元旦将至,为美化路旁风景.现决定用两种不同颜色的花装扮留下来的绿化地.(其中某一种颜色的花摆成一个三角形.)A(1) 如图,若此时D为边AB上一点,要使△ADC∽△ACB,还需要什么条件________________分析:由已知条件可得?A是公共角.解题思路:
有一对应角相等再证一对应角相等或找夹此对应角的两组边对应成比例ADC=?ACB,或?ACD=?ABC唯我争先(2)若用同一花色摆出△ADE,
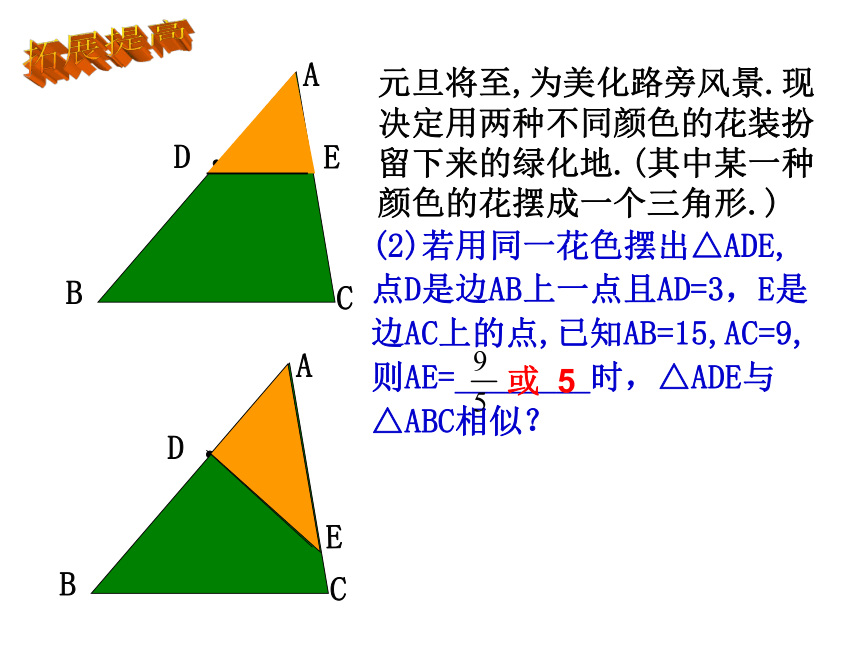
点D是边AB上一点且AD=3,E是边AC上的点,已知AB=15,AC=9,则AE=________时,△ADE与△ABC相似?A元旦将至,为美化路旁风景.现决定用两种不同颜色的花装扮留下来的绿化地.(其中某一种颜色的花摆成一个三角形.)E拓展提高(2)若用同一花色摆出△ADE,
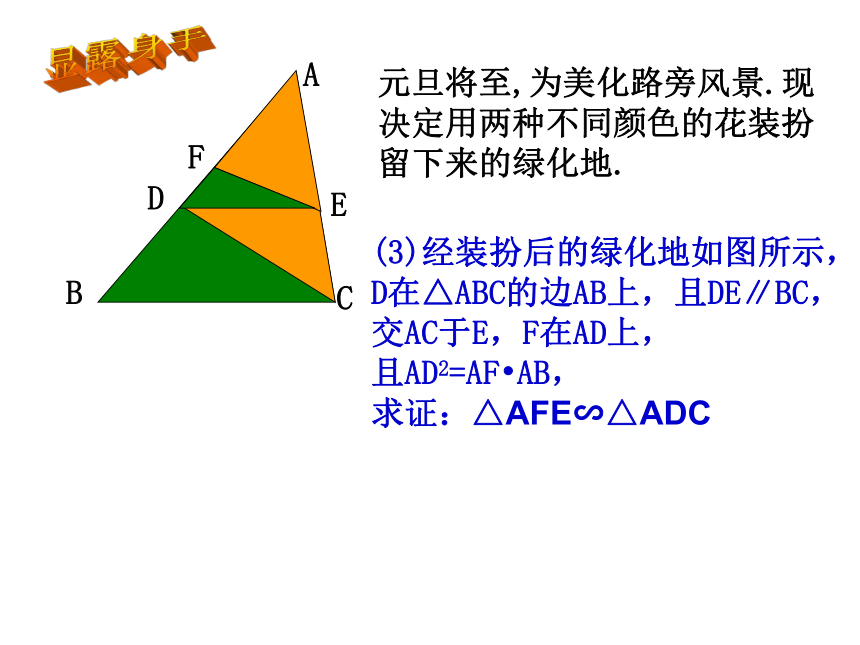
点D是边AB上一点且AD=3,E是边AC上的点,已知AB=15,AC=9,则AE=________时,△ADE与△ABC相似?A元旦将至,为美化路旁风景.现决定用两种不同颜色的花装扮留下来的绿化地.(其中某一种颜色的花摆成一个三角形.)E拓展提高A元旦将至,为美化路旁风景.现决定用两种不同颜色的花装扮留下来的绿化地.(3)经装扮后的绿化地如图所示,D在△ABC的边AB上,且DE∥BC,交AC于E,F在AD上,
且AD2=AF?AB,
求证:△AFE∽△ADC
显露身手分析:
AB是半圆的直径,可得出
∠C是直角,从而可以根据勾股
定理求出AB边的长,再根据三
角形面积公式很快可以得出AB
边上的高线。(1)求△ABC中AB边上的高h分析:
四边形DEFN为矩形,则有
NF∥BC,则△CNF∽△CAB,然
根据相似三角形对应高线的比
等于相似比,就可找到DN与NF
之间的联系。(2)设DN=x,NF=y,求y关于x的
函数关系式;(3)当x为何值时,水池DEFN
的面积最大,其最大面积
是多少?分析:要确定矩形DEFN的最
大面积,就一定要找到矩形面
积与x之间的关系。(4)实际施工时,发现在AB上距B点1.85的M处有一棵大树,
问:这棵大树是否位于最大矩形水池的边上?如果在,为保护
大树,请你设计另外的方案,使内接于满足条件的三角形中欲
建的最大水池能避开大树;如果不在,请说明理由。小结:实际问题数学问题数学问题的解决检验1、2、 数学思想方法: 化归思想、分类讨论.如图,在△ABC中,∠ACB=Rt∠,BC=3,AC=4, PQ∥AB,P点在AC上(与点A、C不重合),Q点在BC上.
(1)当△PQC的面积与四边形PABQ的面积相等时,
求CP的长;
(2)当△PQC的周长与四边形PABQ的周长相等时,
求CP的长;
(3)试问:在AB上是否存在点M,
使得△PQM为等腰直角三角形?
若不存在,请简要说明理由;
若存在,请求出PQ的长。 PQ如图,抛物线 与x轴相交于点A、B,与y轴相交于点C.(1)求证:△AOC∽△COB;(2)过点C作CD∥x 轴交抛物线于
点D.若点P在线段AB上以每秒1个
单位的速度由A向B运动,同时点Q
在线段CD上也以每秒1个单位的速
度由D向C运动,当P到达点A后,运动停止,
连结PQ交CB于点E。E①经过几秒后,S△CEQ=4S△BEP②在运动过程中,当BE:CE=1:4时,请写出E点的坐标. (1)若有平行线----------先考虑预备定理
(2)若可找到两组边成比例
(3)若已有一对应角相等
这节课同学们得到了什么2、性质:相似三角形的高比、周长比等于相似比,面积比等于
相似比的平方. 3、利用相似三角形的有关性质,解决一些实际问题. 1、判定元旦将至,为美化路旁风景.现决定用两种不同颜色的花装扮留下来的绿化地.(其中某一种颜色的花摆成一个三角形.)矩形 继续探索P如图,在△ABC中,四边形DFGE是矩形,已知BC=12,BC边上的高AH=6.(1)若DE:DF=2:1,求DE的长.综合应用HFPG如图,在△ABC中,四边形DFGE是矩形,已知BC=12,BC边上的高AH=6.(1)若DE:DF=2:1,求DE的长.(2)若设DF为x,S矩形DFGE=y,
①写出y关于x的函数关系式,以及自变量x的取值范围?综合应用HFPG如图,在△ABC中,四边形DFGE是矩形,已知BC=12,BC边上的高AH=6.(1)若DE:DF=2:1,求DE的长.(2)若设DF为x,S矩形DFGE=y,
①写出y关于x的函数关系式,以及自变量x的取值范围?②当x为何值时,矩形DFGE的面积最大,最大面积为多少?综合应用HFPG如图,在△ABC中,四边形DFGE是矩形,已知BC=12,BC边上的高AH=6.(3)若矩形DFGE的面积是△ADE的
面积的2倍,求 的值.衷心感谢同学们的合作!
(1)40°80°60 °80°
(2)
(3)
(4)ΔFPQ与ΔFAM的相似比是多少?ΔFPQ与ΔFAM的周长比是多少? 在方格纸中,每个小格的顶点称为格点,以格点的连线为边的三角形称为格点三角形。回忆一下面积比是多少?马路旁边原有一个面积为100平方米,周长为60米的三角形绿化地,
由于改建需要,绿地被削去一个梯形部分作为道路,原绿化地一边长由原来的25米缩短成15米.问1:留下的三角形绿化地与原
三角形绿化地之间有什么
关系?你是如何判断的?梯形小试牛刀 由于改建需要,绿地被削去一个梯形部分作为道路,原绿化地一边长由原来的25米缩短成15米.问1:留下的三角形绿化地与原
三角形绿化地之间有什么
关系?马路旁边原有一个面积为100平方米,周长为60米的三角形绿化地,
问2:留下来的绿化地周长是多少?
面积又是多少?你是如何判断的?25m15m相似三角形的周长比等于相似比,面积比等于相似比的平方. 梯形元旦将至,为美化路旁风景.现决定用两种不同颜色的花装扮留下来的绿化地.(其中某一种颜色的花摆成一个三角形.)A(1) 如图,若此时D为边AB上一点,要使△ADC∽△ACB,还需要什么条件________________分析:由已知条件可得?A是公共角.解题思路:
有一对应角相等再证一对应角相等或找夹此对应角的两组边对应成比例ADC=?ACB,或?ACD=?ABC唯我争先(2)若用同一花色摆出△ADE,
点D是边AB上一点且AD=3,E是边AC上的点,已知AB=15,AC=9,则AE=________时,△ADE与△ABC相似?A元旦将至,为美化路旁风景.现决定用两种不同颜色的花装扮留下来的绿化地.(其中某一种颜色的花摆成一个三角形.)E拓展提高(2)若用同一花色摆出△ADE,
点D是边AB上一点且AD=3,E是边AC上的点,已知AB=15,AC=9,则AE=________时,△ADE与△ABC相似?A元旦将至,为美化路旁风景.现决定用两种不同颜色的花装扮留下来的绿化地.(其中某一种颜色的花摆成一个三角形.)E拓展提高A元旦将至,为美化路旁风景.现决定用两种不同颜色的花装扮留下来的绿化地.(3)经装扮后的绿化地如图所示,D在△ABC的边AB上,且DE∥BC,交AC于E,F在AD上,
且AD2=AF?AB,
求证:△AFE∽△ADC
显露身手分析:
AB是半圆的直径,可得出
∠C是直角,从而可以根据勾股
定理求出AB边的长,再根据三
角形面积公式很快可以得出AB
边上的高线。(1)求△ABC中AB边上的高h分析:
四边形DEFN为矩形,则有
NF∥BC,则△CNF∽△CAB,然
根据相似三角形对应高线的比
等于相似比,就可找到DN与NF
之间的联系。(2)设DN=x,NF=y,求y关于x的
函数关系式;(3)当x为何值时,水池DEFN
的面积最大,其最大面积
是多少?分析:要确定矩形DEFN的最
大面积,就一定要找到矩形面
积与x之间的关系。(4)实际施工时,发现在AB上距B点1.85的M处有一棵大树,
问:这棵大树是否位于最大矩形水池的边上?如果在,为保护
大树,请你设计另外的方案,使内接于满足条件的三角形中欲
建的最大水池能避开大树;如果不在,请说明理由。小结:实际问题数学问题数学问题的解决检验1、2、 数学思想方法: 化归思想、分类讨论.如图,在△ABC中,∠ACB=Rt∠,BC=3,AC=4, PQ∥AB,P点在AC上(与点A、C不重合),Q点在BC上.
(1)当△PQC的面积与四边形PABQ的面积相等时,
求CP的长;
(2)当△PQC的周长与四边形PABQ的周长相等时,
求CP的长;
(3)试问:在AB上是否存在点M,
使得△PQM为等腰直角三角形?
若不存在,请简要说明理由;
若存在,请求出PQ的长。 PQ如图,抛物线 与x轴相交于点A、B,与y轴相交于点C.(1)求证:△AOC∽△COB;(2)过点C作CD∥x 轴交抛物线于
点D.若点P在线段AB上以每秒1个
单位的速度由A向B运动,同时点Q
在线段CD上也以每秒1个单位的速
度由D向C运动,当P到达点A后,运动停止,
连结PQ交CB于点E。E①经过几秒后,S△CEQ=4S△BEP②在运动过程中,当BE:CE=1:4时,请写出E点的坐标. (1)若有平行线----------先考虑预备定理
(2)若可找到两组边成比例
(3)若已有一对应角相等
这节课同学们得到了什么2、性质:相似三角形的高比、周长比等于相似比,面积比等于
相似比的平方. 3、利用相似三角形的有关性质,解决一些实际问题. 1、判定元旦将至,为美化路旁风景.现决定用两种不同颜色的花装扮留下来的绿化地.(其中某一种颜色的花摆成一个三角形.)矩形 继续探索P如图,在△ABC中,四边形DFGE是矩形,已知BC=12,BC边上的高AH=6.(1)若DE:DF=2:1,求DE的长.综合应用HFPG如图,在△ABC中,四边形DFGE是矩形,已知BC=12,BC边上的高AH=6.(1)若DE:DF=2:1,求DE的长.(2)若设DF为x,S矩形DFGE=y,
①写出y关于x的函数关系式,以及自变量x的取值范围?综合应用HFPG如图,在△ABC中,四边形DFGE是矩形,已知BC=12,BC边上的高AH=6.(1)若DE:DF=2:1,求DE的长.(2)若设DF为x,S矩形DFGE=y,
①写出y关于x的函数关系式,以及自变量x的取值范围?②当x为何值时,矩形DFGE的面积最大,最大面积为多少?综合应用HFPG如图,在△ABC中,四边形DFGE是矩形,已知BC=12,BC边上的高AH=6.(3)若矩形DFGE的面积是△ADE的
面积的2倍,求 的值.衷心感谢同学们的合作!
同课章节目录
