数学:浙教版九年级下 22 估计概率(教案)
文档属性
| 名称 | 数学:浙教版九年级下 22 估计概率(教案) |
|
|
| 格式 | rar | ||
| 文件大小 | 24.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-01-07 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
2.2估计概率
教学目标:
1.借助实验,体会随机事件在每一次实验中发生与否具有不确定性;
2.通过操作,体验重复实验的次数与事件发生的频率之间的关系;
3.能从频率值角度估计事件发生的概率;
4.懂得开展实验、设计实验,通过实验数据探索规律,并从中学会合作与交流.
教学重点与难点:通过实验体会用频率估计概率的合理性.
教学过程:
一、引入:
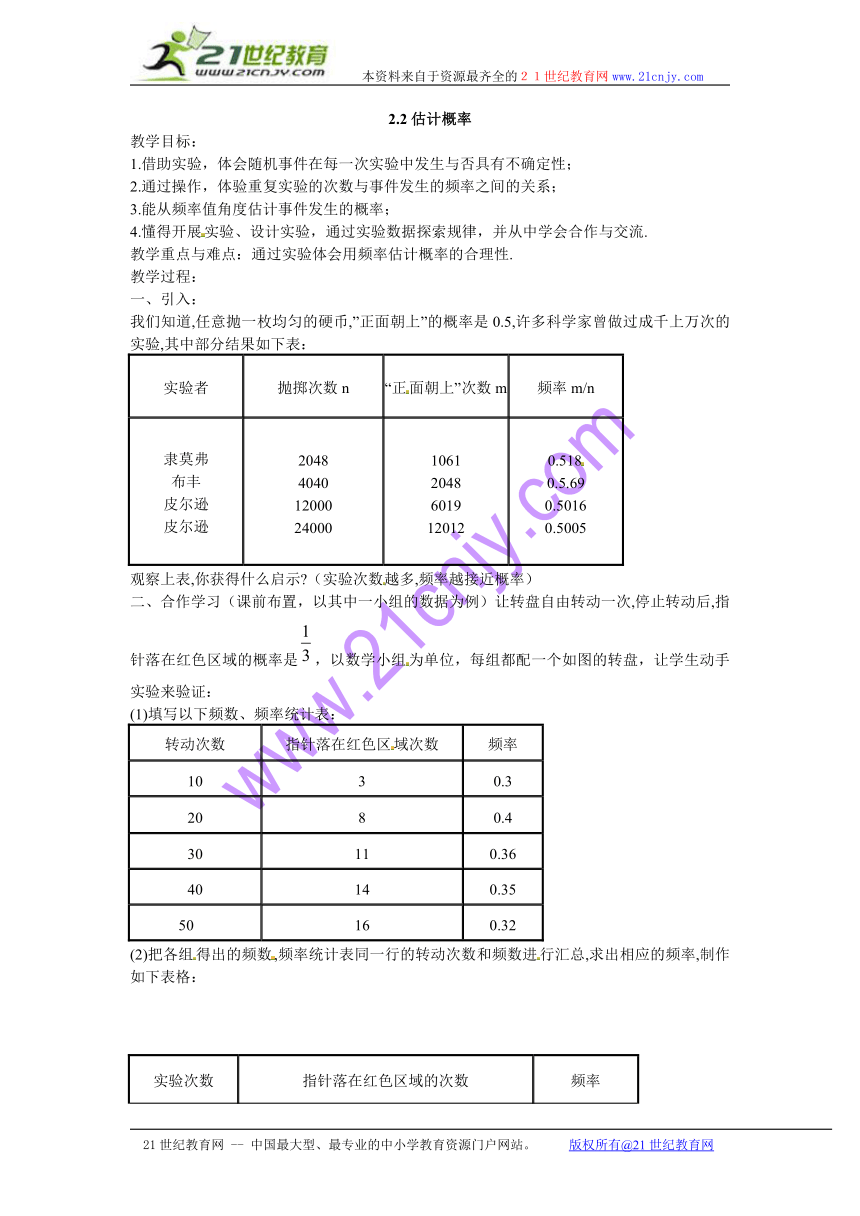
我们知道,任意抛一枚均匀的硬币,”正面朝上”的概率是0.5,许多科学家曾做过成千上万次的实验,其中部分结果如下表:
实验者 抛掷次数n “正面朝上”次数m 频率m/n
隶莫弗布丰皮尔逊皮尔逊 204840401200024000 10612048601912012 0.5180.5.690.50160.5005
观察上表,你获得什么启示 (实验次数越多,频率越接近概率)
二、合作学习(课前布置,以其中一小组的数据为例)让转盘自由转动一次,停止转动后,指针落在红色区域的概率是,以数学小组为单位,每组都配一个如图的转盘,让学生动手实验来验证:
(1)填写以下频数、频率统计表:
转动次数 指针落在红色区域次数 频率
10 3 0.3
20 8 0.4
30 11 0.36
40 14 0.35
5021世纪教育网 16 0.32
(2)把各组得出的频数,频率统计表同一行的转动次数和频数进行汇总,求出相应的频率,制作如下表格:
实验次数 指针落在红色区域的次数 频率
80 25 0.3125
160 58 0.3625
24021世纪教育网 78 0.325
320 110 0.3438
400 130 0.325
(3)根据上面的表格,画出下列频率分布折线图
(4)议一议:频率与概率有什么区别和联系 随着重复实验次数的不断增加,频率的变化趋势如何
结论:从上面的试验可以看到:当重复实验的次数大量增加时,事件发生的频率就稳定在相应的概率附近,因此,我们可以通过大量重复实验,用一个事件发生的频率来估计这一事件发生的概率.
三、做一做:
1.某运动员投篮5次,投中4次,能否说该运动员投一次篮,投中的概率为4/5 为什么
2.回答下列问题:
(1)抽检1000件衬衣,其中不合格的衬衣有2件,由此估计抽1件衬衣合格的概率是多少
(2)1998年,在美国密歇根州汉诺城市的一个农场里出生了1头白色的小奶牛,据统计,平均出生1千万头牛才会有1头是白色的,由此估计出生一头奶牛为白色的概率为多少
四、例题分析:
例1、在同样条件下对某种小麦种子进行发芽实验,统计发芽种子数,获得如下频数分布表:
实验种子n(粒) 1 5 50 100 200 500 1000 2000 3000
发芽频数m(粒) 0 4 45 92 188 476 95121世纪教育网 1900 2850
发芽频数m/n 0
(1)计算表中各个频数.
(2)估计该麦种的发芽概率
(3)如果播种该种小麦每公顷所需麦苗数为4181818棵,种子发芽后的成秧率为87%,该麦种的千粒质量为35g,那么播种3公顷该种小麦,估计约需麦种多少kg
分析:(1)学生根据数据自行计算
(2)估计概率不能随便取其中一个频率区估计概率,也不能以为最后的频率就是概率,而要看频率随实验次数的增加是否趋于稳定.
(3)设需麦种x(kg)
由题意得,
解得 x≈531(kg)
答:播种3公顷该种小麦,估计约需531kg麦种.
五、课内练习:
1.如果某运动员投一次篮投中的概率为0.8,下列说法正确吗 为什么
(1)该运动员投5次篮,必有4次投中.
(2)该运动员投100次篮,约有80次投中.
2.对一批西装质量抽检情况如下:
抽检件数 200 400 600 800 1000 1200
正品件数 190 390 576 773 967 116021世纪教育网
次品的概率 21世纪教育网
(1)填写表格中次品的概率.
(2)从这批西装中任选一套是次品的概率是多少 [来源:21世纪教育网
(3)若要销售这批西装2000件,为了方便购买次品西装的顾客前来调换,至少应该进多少件西装
六、课堂小结:
尽管随机事件在每次实验中发生与否具有不确定性,但只要保持实验条件不变,那么这一事件出现的频率就会随着实验次数的增大而趋于稳定,这个稳定值就可以作为该事件发生概率的估计值.
七、作业:见课课通.
补充:一个口袋中有12个白球和若干个黑球,在不允许将球倒出来数的前提下,小亮为估计口袋中黑球的个数,采用了如下的方法:每次先从口袋中摸出10个球,求出其中白球与10的比值,再把球放回袋中摇匀.不断重复上述过程5次,得到的白求数与10的比值分别为:0.4,0.1,0.2,0.1,0.2.根据上述数据,小亮可估计口袋中大约有 48 个黑球.
(06黑龙江中考题)
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
2.2估计概率
教学目标:
1.借助实验,体会随机事件在每一次实验中发生与否具有不确定性;
2.通过操作,体验重复实验的次数与事件发生的频率之间的关系;
3.能从频率值角度估计事件发生的概率;
4.懂得开展实验、设计实验,通过实验数据探索规律,并从中学会合作与交流.
教学重点与难点:通过实验体会用频率估计概率的合理性.
教学过程:
一、引入:
我们知道,任意抛一枚均匀的硬币,”正面朝上”的概率是0.5,许多科学家曾做过成千上万次的实验,其中部分结果如下表:
实验者 抛掷次数n “正面朝上”次数m 频率m/n
隶莫弗布丰皮尔逊皮尔逊 204840401200024000 10612048601912012 0.5180.5.690.50160.5005
观察上表,你获得什么启示 (实验次数越多,频率越接近概率)
二、合作学习(课前布置,以其中一小组的数据为例)让转盘自由转动一次,停止转动后,指针落在红色区域的概率是,以数学小组为单位,每组都配一个如图的转盘,让学生动手实验来验证:
(1)填写以下频数、频率统计表:
转动次数 指针落在红色区域次数 频率
10 3 0.3
20 8 0.4
30 11 0.36
40 14 0.35
5021世纪教育网 16 0.32
(2)把各组得出的频数,频率统计表同一行的转动次数和频数进行汇总,求出相应的频率,制作如下表格:
实验次数 指针落在红色区域的次数 频率
80 25 0.3125
160 58 0.3625
24021世纪教育网 78 0.325
320 110 0.3438
400 130 0.325
(3)根据上面的表格,画出下列频率分布折线图
(4)议一议:频率与概率有什么区别和联系 随着重复实验次数的不断增加,频率的变化趋势如何
结论:从上面的试验可以看到:当重复实验的次数大量增加时,事件发生的频率就稳定在相应的概率附近,因此,我们可以通过大量重复实验,用一个事件发生的频率来估计这一事件发生的概率.
三、做一做:
1.某运动员投篮5次,投中4次,能否说该运动员投一次篮,投中的概率为4/5 为什么
2.回答下列问题:
(1)抽检1000件衬衣,其中不合格的衬衣有2件,由此估计抽1件衬衣合格的概率是多少
(2)1998年,在美国密歇根州汉诺城市的一个农场里出生了1头白色的小奶牛,据统计,平均出生1千万头牛才会有1头是白色的,由此估计出生一头奶牛为白色的概率为多少
四、例题分析:
例1、在同样条件下对某种小麦种子进行发芽实验,统计发芽种子数,获得如下频数分布表:
实验种子n(粒) 1 5 50 100 200 500 1000 2000 3000
发芽频数m(粒) 0 4 45 92 188 476 95121世纪教育网 1900 2850
发芽频数m/n 0
(1)计算表中各个频数.
(2)估计该麦种的发芽概率
(3)如果播种该种小麦每公顷所需麦苗数为4181818棵,种子发芽后的成秧率为87%,该麦种的千粒质量为35g,那么播种3公顷该种小麦,估计约需麦种多少kg
分析:(1)学生根据数据自行计算
(2)估计概率不能随便取其中一个频率区估计概率,也不能以为最后的频率就是概率,而要看频率随实验次数的增加是否趋于稳定.
(3)设需麦种x(kg)
由题意得,
解得 x≈531(kg)
答:播种3公顷该种小麦,估计约需531kg麦种.
五、课内练习:
1.如果某运动员投一次篮投中的概率为0.8,下列说法正确吗 为什么
(1)该运动员投5次篮,必有4次投中.
(2)该运动员投100次篮,约有80次投中.
2.对一批西装质量抽检情况如下:
抽检件数 200 400 600 800 1000 1200
正品件数 190 390 576 773 967 116021世纪教育网
次品的概率 21世纪教育网
(1)填写表格中次品的概率.
(2)从这批西装中任选一套是次品的概率是多少 [来源:21世纪教育网
(3)若要销售这批西装2000件,为了方便购买次品西装的顾客前来调换,至少应该进多少件西装
六、课堂小结:
尽管随机事件在每次实验中发生与否具有不确定性,但只要保持实验条件不变,那么这一事件出现的频率就会随着实验次数的增大而趋于稳定,这个稳定值就可以作为该事件发生概率的估计值.
七、作业:见课课通.
补充:一个口袋中有12个白球和若干个黑球,在不允许将球倒出来数的前提下,小亮为估计口袋中黑球的个数,采用了如下的方法:每次先从口袋中摸出10个球,求出其中白球与10的比值,再把球放回袋中摇匀.不断重复上述过程5次,得到的白求数与10的比值分别为:0.4,0.1,0.2,0.1,0.2.根据上述数据,小亮可估计口袋中大约有 48 个黑球.
(06黑龙江中考题)
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
