浙教版八年级上《一次函数》复习课件

课件28张PPT。 时间是一个“常量”，
但对于勤奋者来说，
却是一个“变量”……
你的收获与你的付出是成正比的，
一份耕耘一份收获，
相信自己，只要付出，
你一定会有收获！ 一次函数复习1变量与常量：
在某个变化过程中保持不变的量叫常量；
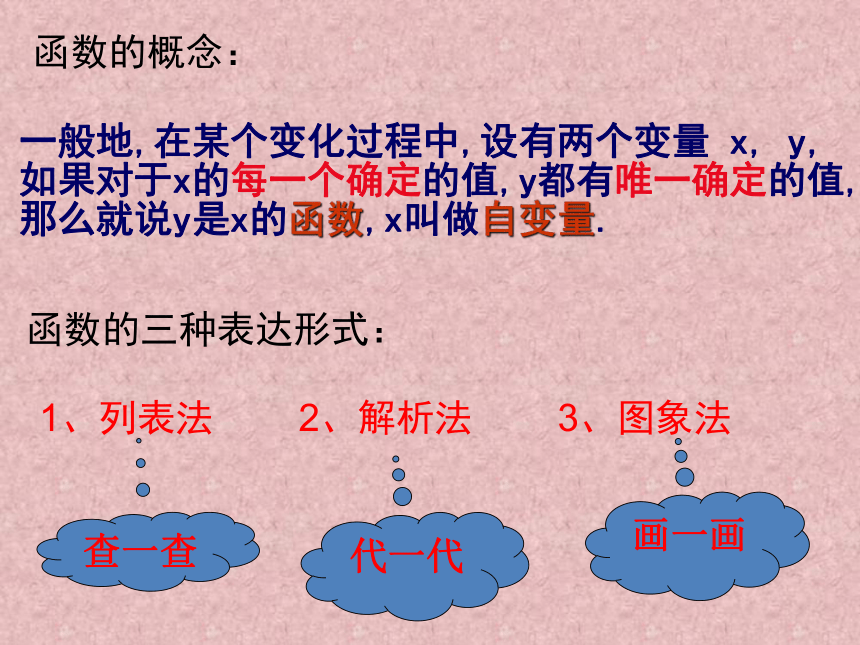
在某个变化过程中变化的量叫变量。例1、环卫工作人员在清扫长10km街道时，路程、效率、时间中哪些是变量，哪些是常量。 环卫工作人员在2km/小时的速度清扫街道时，路程、速度、时间中哪些是变量，哪些是常量。 环卫工作人员用了4小时清扫一条街道时，路程、效率、时间中哪些是变量，哪些是常量。函数的三种表达形式：1、列表法 2、解析法 3、图象法函数的概念：一般地,在某个变化过程中,设有两个变量 x, y,如果对于x的每一个确定的值,y都有唯一确定的值, 那么就说y是x的函数,x叫做自变量.
查一查代一代画一画 函数y=_______(k、b为常数，k______)叫做一次函数。当b_____时，函数y=____(k____)叫做正比例函数。★理解一次函数概念应注意下面两点：
⑴、解析式中自变量x的次数是___次，
⑵、比例系数_____。一次函数的概念：kx ＋b≠０ = ０≠０kx1K≠0 1、正比例函数y=kx(k≠0)的图象是过点（_____），(______)的_________。
2、一次函数y=kx+b(k≠0)的图象是过点（0，___),（____，0)的__________。一次函数的性质：0，01，kb 一条直线一条直线3、正比例函数y=kx（k≠0)的性质：
　　⑴当k>0时，图象过______象限；y随x的增大而____。
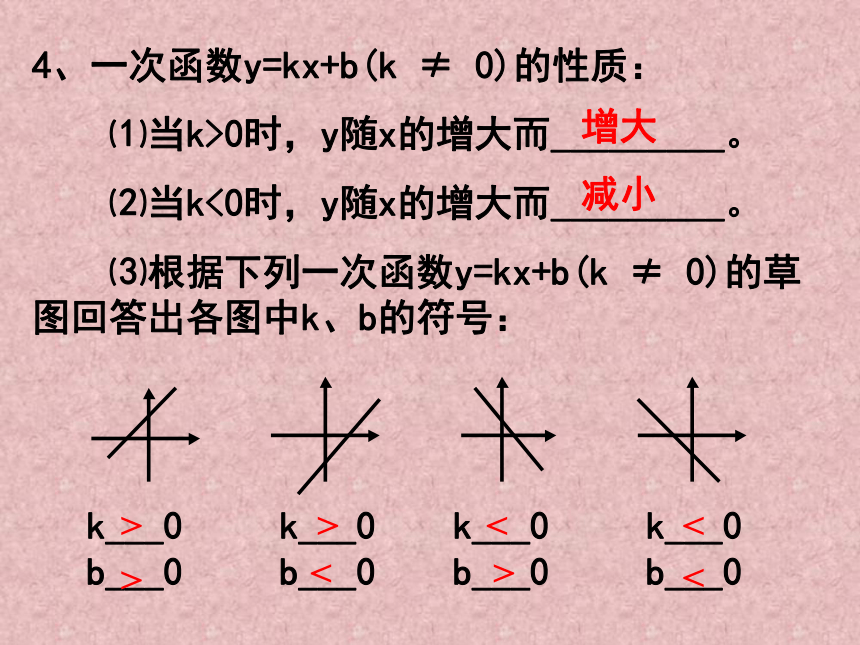
　　⑵当k<0时，图象过______象限；y随x的增大而____。一、三增大二、四减小4、一次函数y=kx+b(k ≠ 0)的性质：
　　⑴当k>0时，y随x的增大而_________。
　　⑵当k<0时，y随x的增大而_________。
　　⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图中k、b的符号：增大减小<<><<>>>例2、填空题：
　　有下列函数：①　　　　　　②　　
③　　　 ④ 。其中过原点的直线是_____；函数y随x的增大而增大的是___________；函数y随x的增大而减小的是______；图象在第一、二、三象限的是_____。④①②④③②例3、已知一次函数y=kx+b(k≠0)在x=1时，y=5，且它的图象与x轴交点的横坐标是６，求这个一次函数的解析式。点评：用待定系数法求一次函数y=kx+b的解析式，可由已知条件给出的两对x、y的值，列出关于k、b的二元一次方程组。由此求出k、b的值，就可以得到所求的一次函数的解析式。例4、已知y-1与x成正比例，且x=－2时，y=4，那么y与x之间的函数关系式为_________________。例5、已知一次函数的图像经过点A（2，－1）
和点B，其中点B是另一条直线
与y轴的交点，求这个一次函数的表达式。例6：直线y=kx+b经过点（-2，5），图象与y轴的交点和直线y=2x+3与y轴的交点关于x轴对称，求这个一次函数的解析式。例7、已知一条直线与直线 y=2x+1的交点的横坐标为2，且与直线y=-x-8的交点坐标为-7，求这条直线的解析式。例8、在平面直角坐标系中，有一条线段的解析式为y=ax+b，其中a≠0，当-2≤x≤6，函数值的取值范围为-11≤y≤9，求这条线段所在直线的解析式。例9、已知一次函数图形与正比例函数图象y=3x平行，且经过点（2，6），求这一次函数的解析式。例10、已知y=kx+b过一、二、三象限，且与x轴、y轴的交点坐标分别是A（t，0），B（0，4），若△AOB的面积是6，求这个一次函数的解析式。直线y=kx+b与坐标轴围
成的三角形面积的计算 例11、已知：函数y = (m+1) x+2 m﹣6
（1）若函数图象过（﹣1 ，2），求此函数的
解析式。
（2）若函数图象与直线 y = 2 x + 5 平行，
求其函数的解析式。
（3）求满足（2）条件的直线与此同时y =
﹣3 x + 1 的交点并求这两条直线 与y 轴所围成
的三角形面积 例12、已知一次函数 y=（6+3m）x+n-4，求:
（1）m为何值时，y随x的增大而减小？
（2）n为何值时，函数图象与y轴交点在x轴的下方？
（3）m, n 分别为何值时，函数图象经过 (0，0).
（4）若m=1，n=9时，当x为何值时，y≥0；
当y为何值时，x＜0例13、 一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h(厘米)与燃烧时间t(时)的函数关系的图象是( ) ACBD例14、某植物t天后的高度为ycm,图中反映了y与t之间的关系，根据图象回答下列问题：(1)植物刚栽的时候多高？9631215182124l2468101214t/天Y cm（2）3天后该植物高度为多少？（3）几天后该植物高度可达 21cm?（4）先写出y与t的关系式，
再计算长到100cm需几天？例15、如图，x 轴：托运行李的重量；y 轴：托运行李的费用，射线AB、CD分别表示甲、乙两航空公司（在相同里程的情况下）托运行李的费用与托运行李的重量之间的函数关系.甲40D15050250A80C0BY（元）X（千克）甲乙你从图象中可以得出哪些信息？（1）设整齐摆放在桌面上饭碗的高度为y (cm),
饭碗数为x (个),求 y与x之间的一次函数
解析式.（2）把这两摞饭碗整齐地摆成一摞时，这摞
饭碗的高度是多少？
例16、相同规格的饭碗整齐地叠放在桌上例17、为迎接校运动会，七年级（2）班的李进同学每天早上都与爸爸一起参加长跑训练，他们沿相同的路线从家里跑到学校，两人所跑的路程s与时间t之间的函数关系如图所示，(假设两人均为匀速运动) 请思考:爸爸追上李进需 要几分钟？李进家到学校 的距离为多少米？李进 跑到学校需要几分钟？ 你能从图象中直接获取哪些信息呢?与周围同学交流一下吧!并展示你的成果.例18、清华大学登山队某队员在攀登念青唐古拉中央峰时，其距离地面的海拔高度s（米）与时间t（小时）之间的函数关系如图所示。(假设往返均为匀速运动)
（1）你能分别求出t≤12和t＞12时s与t的函数关系式吗? S1＝400t（t≤12）
S2＝－600t+12000（t＞12） OA所在的直线是什么函数? AB呢?请解答!（2）一般情况下，人到达海拔3000米左右地区时,就开始出现呼吸频率和心率加快、疲乏、头痛等不良症状，那么运动员在这次登山运动中出现这种症状大约会持续多久?例19、如图，l1、l2分别表示 一种白炽灯和一种节能灯的费用(灯的售价和电费)y(元)与照明时间x(h)的函数图象，假设两种灯的使用寿命都是2000h，照明效果一样。
(1)根据图象分别求出
l1、l2的函数关系式；(2)当照明时间为多少小时时，两种灯的使用寿命相等？例19、如图，l1、l2分别表示 一种白炽灯和
一种节能灯的费用(灯的售价和电费)y
(元)与照明时间x(h)的函数图象，假设两
种灯的使用寿命都是2000h，照明效果一
样。
(3)小明的房间计划
照明2500h，他买了
一个白炽灯和一个
节能灯，请你帮他
设计最省钱的用灯方式。例20、从A、B两水库向甲、乙两地调水，其中甲地需水15万吨，乙地需水13万吨，A、B两地各可调出水14万吨。从A到甲地50千米，到乙地30千米；从B地到甲地60千米，到乙地45千米。设计一个调运方案使水的调运量(单位：万吨·千米)最小。例21、A、B两个商场平时以同样的价格出售相同的商品，在春节期间让利酬宾，A商场所有的商品8折出售；B商场消费金额超过200元后，可在这家商场7折购物。试问如何选择商场来购物更经济？例22、某运输公司根据需要，计划构进大、
中型客车共10辆，大型客车每辆价格25万元，中型客车每辆价格15万元。
(1)若设购买大型客车x辆，购车总费用
为y万元，求y与x之间的函数解析式；
(2)若购车资金为180至200万元(含180和200万元)，在确保交通安全的前提下，
根据客流量的调查结果，大型客车应不少于4辆，此时如何确定购车方案可使运输该公司购车费用最少？例23如图，已知函数 y=ax+b 和 y=kx的图象交于点P, 则根据图象可得，关于的二元一次方程组的解 是 ． 例24、某医药研究所开发了一种新药，在实际验药时发现，如果成人按规定剂量服用，那么每毫升血液中含药量y（毫克）随 时间x（时）的变化情况 如图所示，当成年人按 规定剂量服药后。
（1）服药后______时，
血液中含药量最高，达到每毫升
_______毫克，接着逐步衰弱。
（2）服药5时，血液中含药量为每毫升____毫克。263（3）当x≤2时y与x之间的函数关系式是_________.
（4）当x≥2时y与x之间的函数关系式是___________
（5）如果每毫升血液中含药量3毫克或3毫克以上时，治疗疾病最有效，那么这个有效时间范围是___时。.4y= -x+8y= 3x