7.4一次函数的图象(1)
图片预览




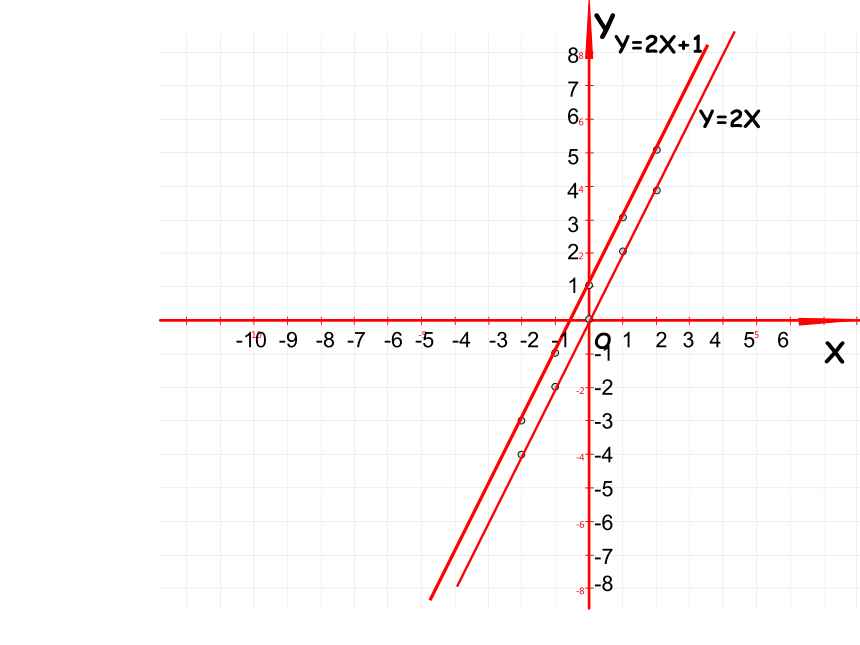

文档简介
课件21张PPT。7.4.1一次函数的图象 若两个变量x,y间的关系式可以表示成y=kx+b(k,b为常数,k不为零)的形式,则称y是x的一次函数 . 其中x为自变量. 特别地,当b=0时,称y是x的正比例函数.1.什么叫一次函数?
2、函数有哪几种表示方式?列表法、解析式法、图象法。解析法:y=5x, y=-2x+3……,表示函数关系的等式;
列表法:
把自变量x的一系列值和函数y的对应值列成一个表;
图象法:如图1, 图象(粗线)表示速度
一定的情况下路程S(米) 与时间t(秒)之
间的函数关系。
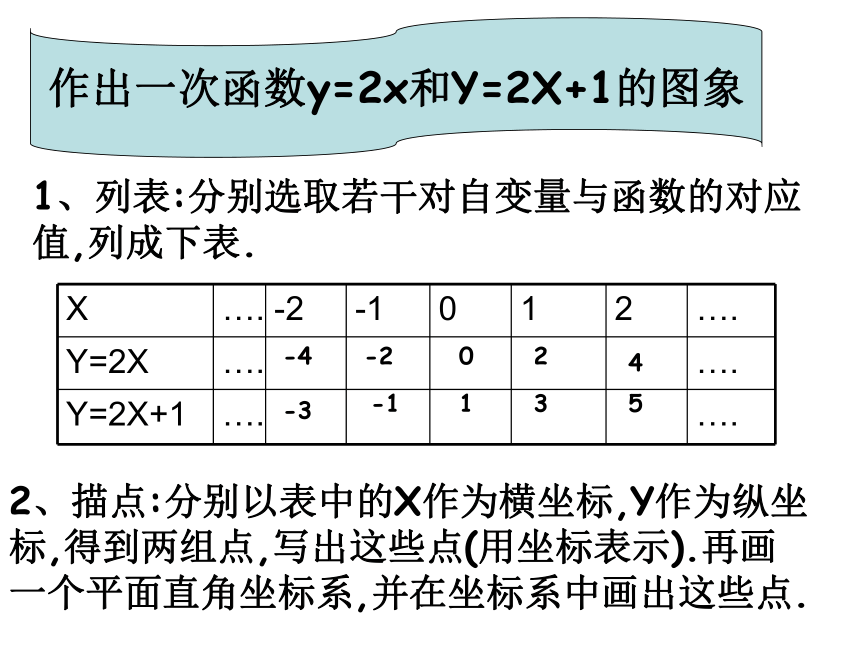
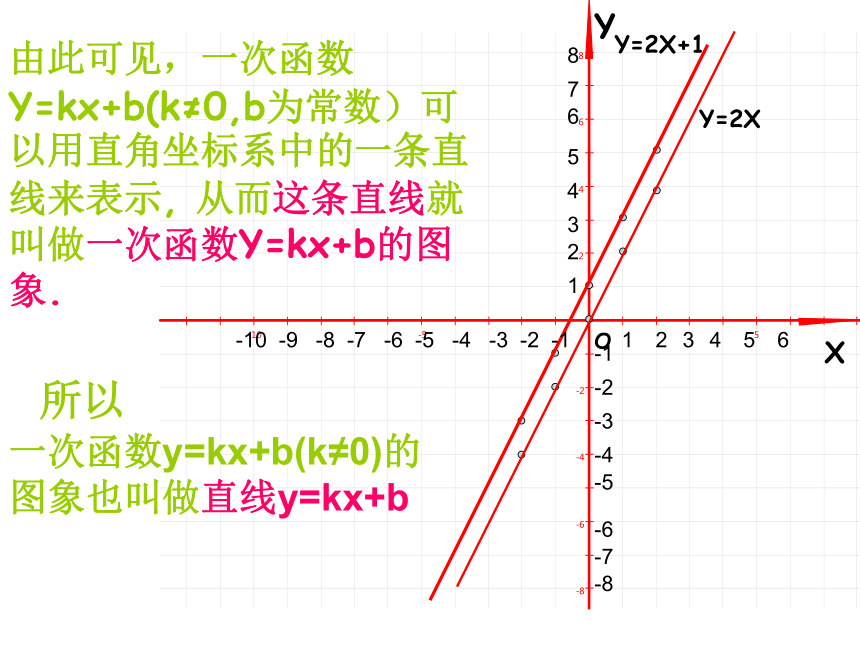
把一个函数的自变量x与对应的函数y的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做函数的图象。 函 数的 图 象作出一次函数y=2x和Y=2X+1的图象1、列表:分别选取若干对自变量与函数的对应值,列成下表.2、描点:分别以表中的X作为横坐标,Y作为纵坐标,得到两组点,写出这些点(用坐标表示).再画一个平面直角坐标系,并在坐标系中画出这些点.-4-3-2-1012345YXOY=2XY=2X+1 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1-1-2-3-4-5-612345612345678-7-8YXOY=2X+12.在你所画的直线上再取几个点,分别找出各点的横坐标和纵坐标,检验一下这些点的坐标是否 满足关系式y=2x+1 ? -10 -9 -8 -7 -6 -5 -4 -3 -2 -1-1-2-3-4-5-612345612345678-7-81.请你再找出另外一些满足一次函数y=2x+1的数对出来,看一看以这些数对为坐标的点在不在所画的直线上?YXOY=2XY=2X+1由此可见,一次函数Y=kx+b(k≠0,b为常数)可以用直角坐标系中的一条直线来表示, 从而这条直线就叫做一次函数Y=kx+b的图象. -10 -9 -8 -7 -6 -5 -4 -3 -2 -1-1-2-3-4-5-612345612345678-7-8一次函数y=kx+b(k≠0)的图象也叫做直线y=kx+b所以例1:在同一坐标系作出下列函数
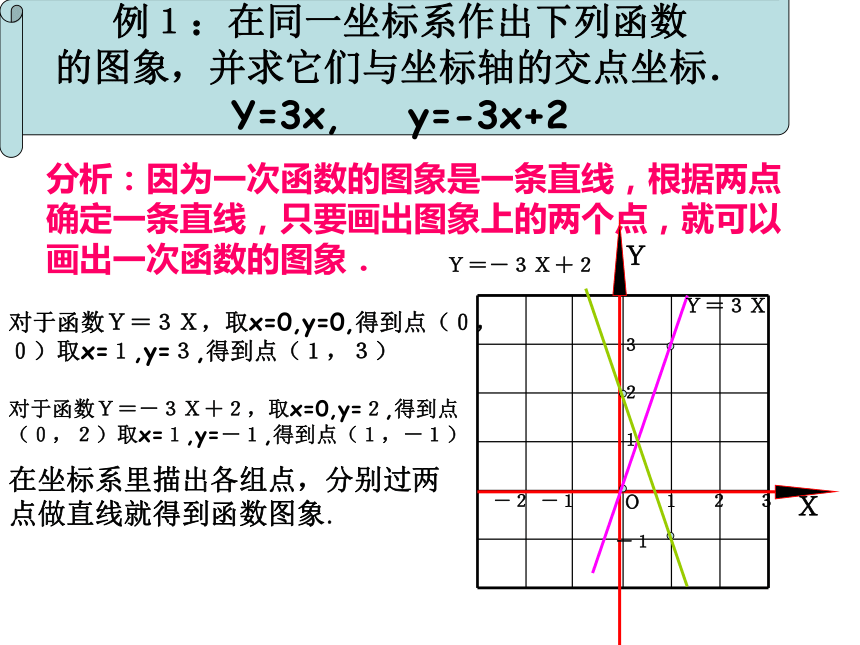
的图象,并求它们与坐标轴的交点坐标.
Y=3x, y=-3x+2分析:因为一次函数的图象是一条直线,根据两点确定一条直线,只要画出图象上的两个点,就可以画出一次函数的图象.对于函数Y=3X,取x=0,y=0,得到点(0,0)取x=1,y=3,得到点(1,3)对于函数Y=-3X+2,取x=0,y=2,得到点(0,2)取x=1,y=-1,得到点(1,-1)在坐标系里描出各组点,分别过两点做直线就得到函数图象.YXO123123-1-1-2Y=3XY=-3X+2归纳: 练 一 练(1(A)(0,3) (B)(1,1)
(C)(2,1) (D)( -1,5)C例2: (1)若点(a,3)在直线y=2x-5上,则a=______(2)若点(2,-3)在直线y=kx+7上,则k=______4-5例3:一次函数的图象过M(3,2),N(-1, - 6)(1)求函数的解析式;(2)试判断点P(2a,4a-4)是否在函数的图象上,并说明理由;思考:一次函数y=2x-5的如象如图所示,你能求出直线y=2x-5与坐标轴的交点坐标吗?求直线与x轴交点坐标:令y=0
求直线与y轴交点坐标:令x=0(2.5,0)(0,-5)例4:已知一次函数y=-2x+6。 (1)求该函数的图象与坐标轴交点的坐标。(2)画出该函数的图象。
例5.已知直线y= -2x+4,它与x轴的交点为A,与y轴的交点为B.
(1).求A, B两点的坐标.
(2).求?AOB的面积. (O为坐标原点)练一练:1.函数y=2x+3的图象是( )
(A)过点(0,3),(0,- 1.5 )的直线
(B)过点(0,- 1.5 ),(1,5)的直线
(C)过点(- 1.5 ,0),(-1,1)的直线
(D)过点(0,3),( 1.5 ,0)的直线
2、已知函数y=-8x+16,求该函数图象与y轴的交点是 ,
与x轴的交点是 ;
3、已知函数 y=-2x+6,则它的图象形状是 ,
图象与坐标轴围成的三角形面积是 .
4、已知函数y=kx-2过点(1,1),则k= .
5、已知点(a,4)在直线y=x-2上,则a= .
6、不论k取何值,直线 y=kx+5一定经过的点是 .C(0 , 16)(2 , 0)一条直线936(0 , 5)注意:
画函数图象时要注意自变量的取值范围.梳理一下吧! 2、函数图象的概念包含两个方面的内容:
(1)满足函数解析式的任意一对x、y的值描出的点一定
在这个函数的图象上。
(2)在函数图象上的点A(x,y)中的x、y一定满足函
数的解析式。1、函数图象的概念: 把一个函数的自变量x与对应的函数y的值分别作
为点的横坐标和纵坐标 , 在直角坐标系内描出它的对 应点 , 所有这些点组成的图形叫做该函数的图象. 3、作函数图象的一般步骤:(1)列表; (2)描点;(3)连线 由此结论可知画一次函数图象的方法可用两点法——一般取满足函数解析式的较方便的两个点,再连成直线即可。6、函数的代数表达式与函数图象是紧密联系着的,“数”用“形”表示,由“形”想到“数”,这是我们数学学习中一个很重要的思想方法——数形结合。 一次函数y=kx+b(k≠0)的图象是一条直线 。
所以一次函数y=kx+b的图象也叫做直线y=kx+b。4、一次函数的图象特征和画法:5、画函数图象时还应特别注意:需考虑自变量的取值范围。
2、函数有哪几种表示方式?列表法、解析式法、图象法。解析法:y=5x, y=-2x+3……,表示函数关系的等式;
列表法:
把自变量x的一系列值和函数y的对应值列成一个表;
图象法:如图1, 图象(粗线)表示速度
一定的情况下路程S(米) 与时间t(秒)之
间的函数关系。
把一个函数的自变量x与对应的函数y的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做函数的图象。 函 数的 图 象作出一次函数y=2x和Y=2X+1的图象1、列表:分别选取若干对自变量与函数的对应值,列成下表.2、描点:分别以表中的X作为横坐标,Y作为纵坐标,得到两组点,写出这些点(用坐标表示).再画一个平面直角坐标系,并在坐标系中画出这些点.-4-3-2-1012345YXOY=2XY=2X+1 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1-1-2-3-4-5-612345612345678-7-8YXOY=2X+12.在你所画的直线上再取几个点,分别找出各点的横坐标和纵坐标,检验一下这些点的坐标是否 满足关系式y=2x+1 ? -10 -9 -8 -7 -6 -5 -4 -3 -2 -1-1-2-3-4-5-612345612345678-7-81.请你再找出另外一些满足一次函数y=2x+1的数对出来,看一看以这些数对为坐标的点在不在所画的直线上?YXOY=2XY=2X+1由此可见,一次函数Y=kx+b(k≠0,b为常数)可以用直角坐标系中的一条直线来表示, 从而这条直线就叫做一次函数Y=kx+b的图象. -10 -9 -8 -7 -6 -5 -4 -3 -2 -1-1-2-3-4-5-612345612345678-7-8一次函数y=kx+b(k≠0)的图象也叫做直线y=kx+b所以例1:在同一坐标系作出下列函数
的图象,并求它们与坐标轴的交点坐标.
Y=3x, y=-3x+2分析:因为一次函数的图象是一条直线,根据两点确定一条直线,只要画出图象上的两个点,就可以画出一次函数的图象.对于函数Y=3X,取x=0,y=0,得到点(0,0)取x=1,y=3,得到点(1,3)对于函数Y=-3X+2,取x=0,y=2,得到点(0,2)取x=1,y=-1,得到点(1,-1)在坐标系里描出各组点,分别过两点做直线就得到函数图象.YXO123123-1-1-2Y=3XY=-3X+2归纳: 练 一 练(1
(C)(2,1) (D)( -1,5)C例2: (1)若点(a,3)在直线y=2x-5上,则a=______(2)若点(2,-3)在直线y=kx+7上,则k=______4-5例3:一次函数的图象过M(3,2),N(-1, - 6)(1)求函数的解析式;(2)试判断点P(2a,4a-4)是否在函数的图象上,并说明理由;思考:一次函数y=2x-5的如象如图所示,你能求出直线y=2x-5与坐标轴的交点坐标吗?求直线与x轴交点坐标:令y=0
求直线与y轴交点坐标:令x=0(2.5,0)(0,-5)例4:已知一次函数y=-2x+6。 (1)求该函数的图象与坐标轴交点的坐标。(2)画出该函数的图象。
例5.已知直线y= -2x+4,它与x轴的交点为A,与y轴的交点为B.
(1).求A, B两点的坐标.
(2).求?AOB的面积. (O为坐标原点)练一练:1.函数y=2x+3的图象是( )
(A)过点(0,3),(0,- 1.5 )的直线
(B)过点(0,- 1.5 ),(1,5)的直线
(C)过点(- 1.5 ,0),(-1,1)的直线
(D)过点(0,3),( 1.5 ,0)的直线
2、已知函数y=-8x+16,求该函数图象与y轴的交点是 ,
与x轴的交点是 ;
3、已知函数 y=-2x+6,则它的图象形状是 ,
图象与坐标轴围成的三角形面积是 .
4、已知函数y=kx-2过点(1,1),则k= .
5、已知点(a,4)在直线y=x-2上,则a= .
6、不论k取何值,直线 y=kx+5一定经过的点是 .C(0 , 16)(2 , 0)一条直线936(0 , 5)注意:
画函数图象时要注意自变量的取值范围.梳理一下吧! 2、函数图象的概念包含两个方面的内容:
(1)满足函数解析式的任意一对x、y的值描出的点一定
在这个函数的图象上。
(2)在函数图象上的点A(x,y)中的x、y一定满足函
数的解析式。1、函数图象的概念: 把一个函数的自变量x与对应的函数y的值分别作
为点的横坐标和纵坐标 , 在直角坐标系内描出它的对 应点 , 所有这些点组成的图形叫做该函数的图象. 3、作函数图象的一般步骤:(1)列表; (2)描点;(3)连线 由此结论可知画一次函数图象的方法可用两点法——一般取满足函数解析式的较方便的两个点,再连成直线即可。6、函数的代数表达式与函数图象是紧密联系着的,“数”用“形”表示,由“形”想到“数”,这是我们数学学习中一个很重要的思想方法——数形结合。 一次函数y=kx+b(k≠0)的图象是一条直线 。
所以一次函数y=kx+b的图象也叫做直线y=kx+b。4、一次函数的图象特征和画法:5、画函数图象时还应特别注意:需考虑自变量的取值范围。
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
