特殊四边形

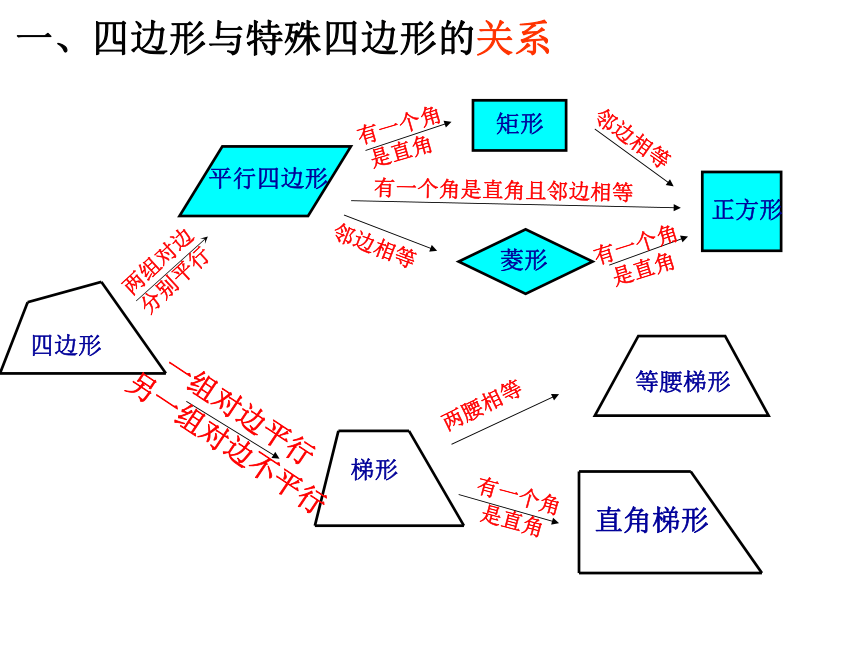
课件107张PPT。特殊四边形一、四边形与特殊四边形的关系　四边形平行四边形矩形菱形正方形梯形等腰梯形直角梯形两组对边
分别平行有一个角
是直角邻边相等邻边相等有一个角
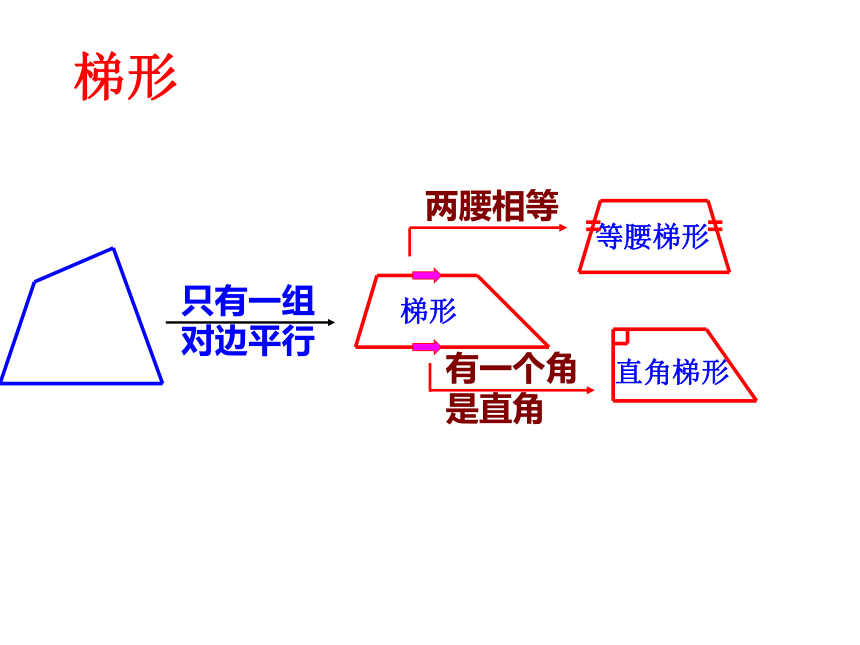
是直角 一组对边平行
另一组对边不平行两腰相等 有一个角
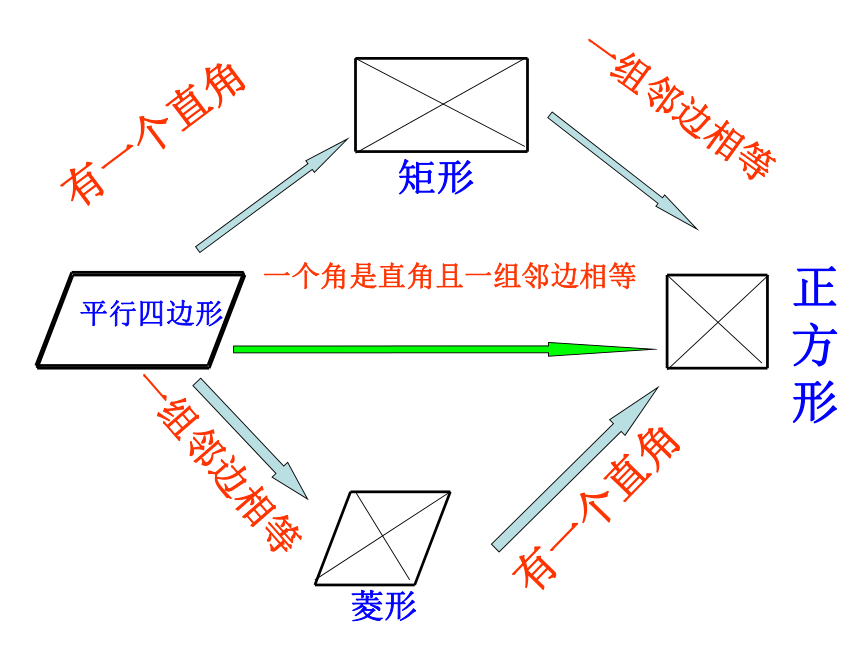
是直角有一个角是直角且邻边相等有一个直角一组邻边相等一组邻边相等有一个直角一个角是直角且一组邻边相等正方形平行四边形矩形菱形只有一组
对边平行两腰相等有一个角
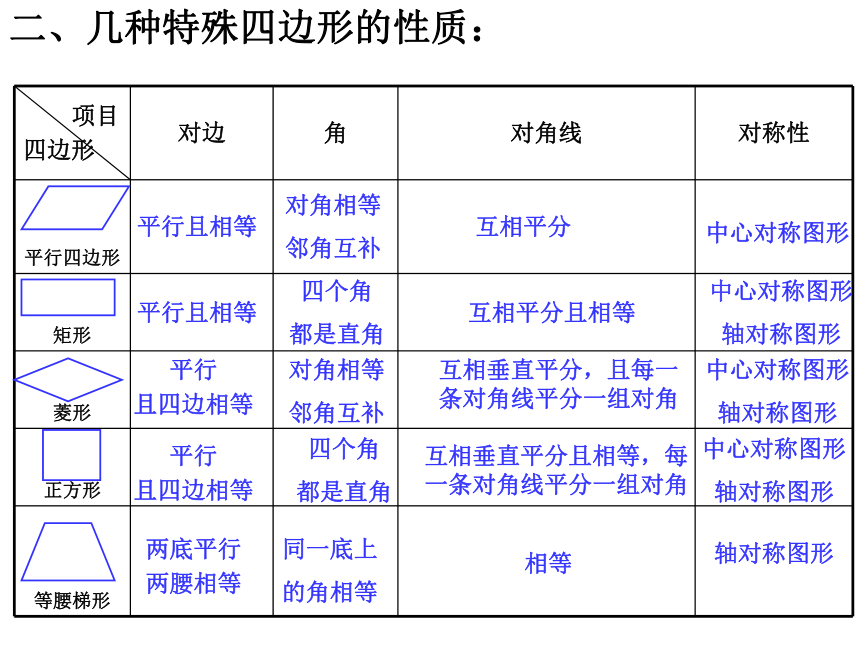
是直角梯形平行且相等平行且相等平行
且四边相等平行
且四边相等两底平行
两腰相等对角相等
邻角互补四个角
都是直角同一底上
的角相等对角相等
邻角互补四个角
都是直角互相平分互相平分且相等互相垂直平分，且每一条对角线平分一组对角相等互相垂直平分且相等，每一条对角线平分一组对角中心对称图形中心对称图形
轴对称图形中心对称图形
轴对称图形中心对称图形
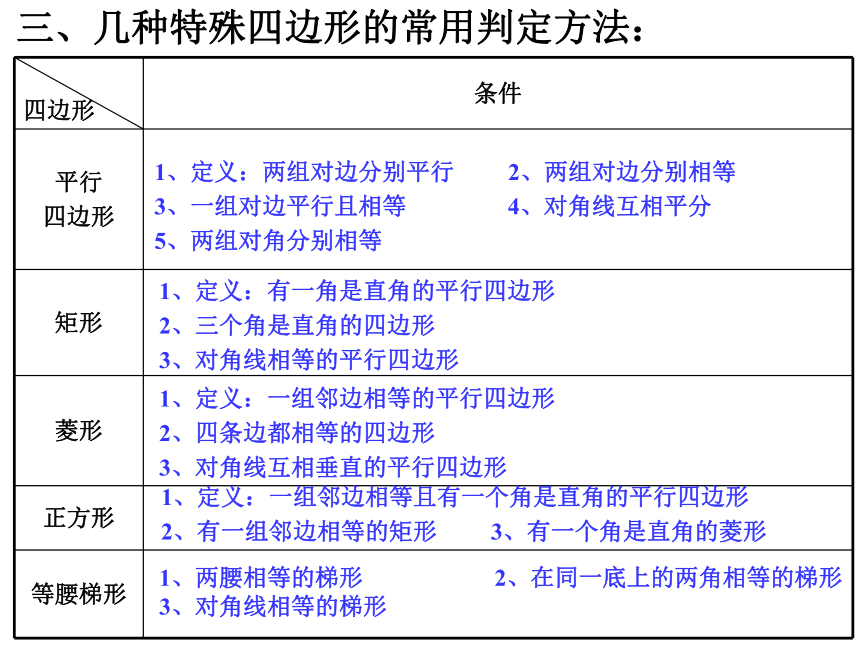
轴对称图形轴对称图形二、几种特殊四边形的性质：三、几种特殊四边形的常用判定方法：1、定义：两组对边分别平行 2、两组对边分别相等
3、一组对边平行且相等 4、对角线互相平分
5、两组对角分别相等1、定义：有一角是直角的平行四边形
2、三个角是直角的四边形
3、对角线相等的平行四边形1、定义：一组邻边相等的平行四边形
2、四条边都相等的四边形
3、对角线互相垂直的平行四边形1、定义：一组邻边相等且有一个角是直角的平行四边形
2、有一组邻边相等的矩形 3、有一个角是直角的菱形
1、两腰相等的梯形 2、在同一底上的两角相等的梯形 3、对角线相等的梯形（四）其它重要定理： 图形 内角和 外角和
三角形：
四边形：
n边形： （2）两条平行线之间的垂线段处处相等

（3）直角三角形斜边上的中线等于斜边的一半。

（1）内角和、外角和定理： 180° 360°
360° 360 °
（n-2）180° 360° 四边形复习课（五）特殊四边形的面积：
（1） S平行四边形 = 底?高
（2） S矩形 = 长?宽
（3） S菱形 = 底?高
（4） S正方形 = 边长2
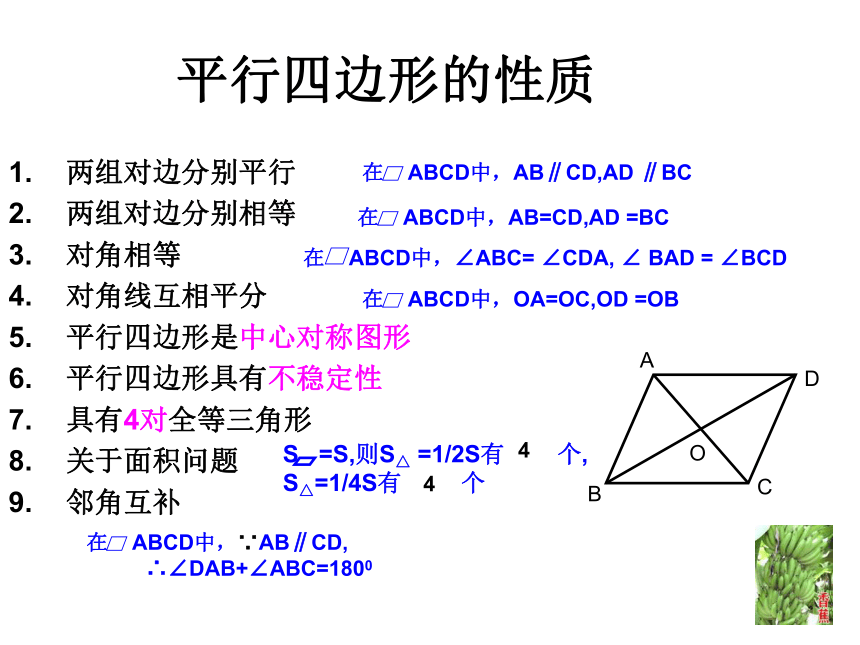
（5） S梯形 =（上底+下底）?高?2= 对角线之积的一半平行四边形的性质两组对边分别平行
两组对边分别相等
对角相等
对角线互相平分
平行四边形是中心对称图形
平行四边形具有不稳定性
具有4对全等三角形
关于面积问题
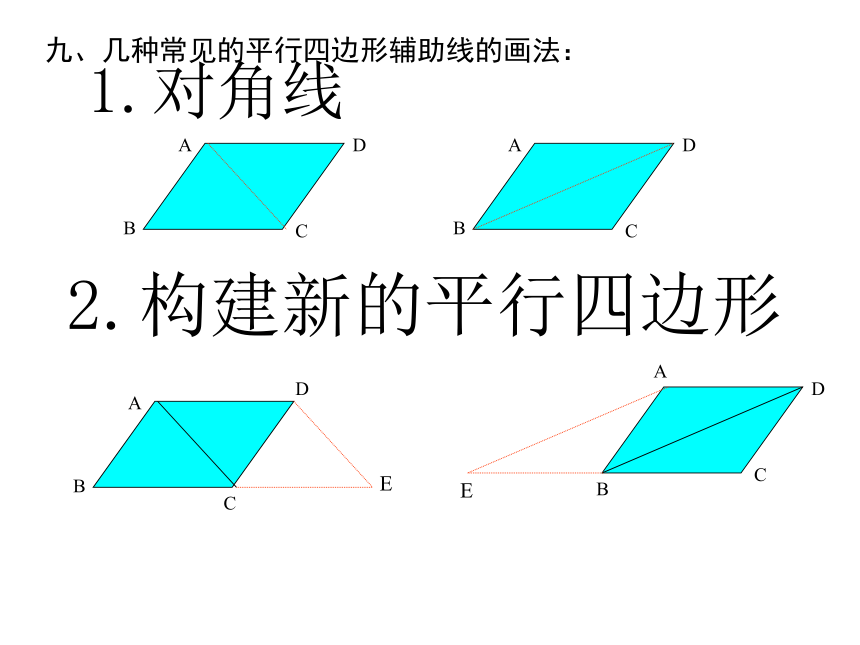
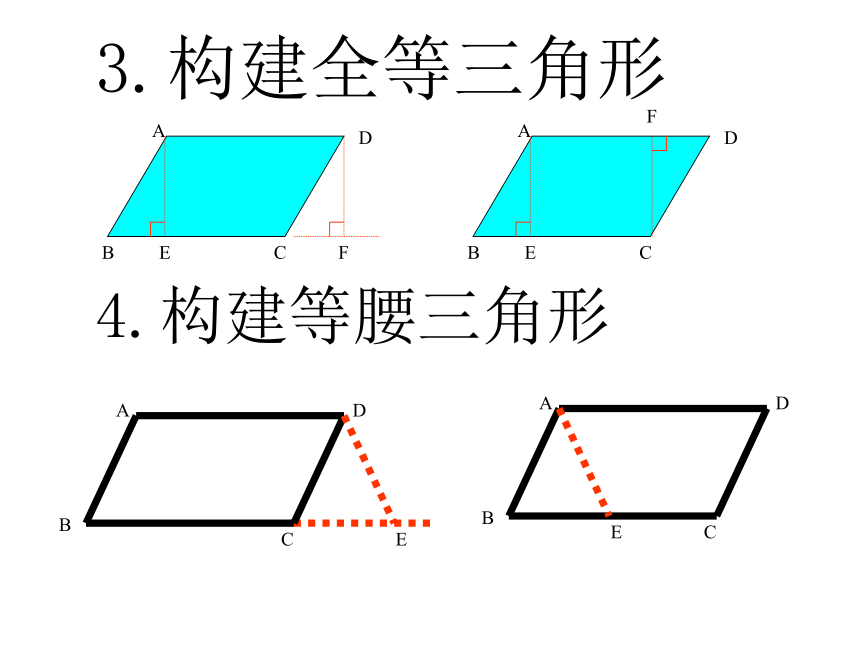
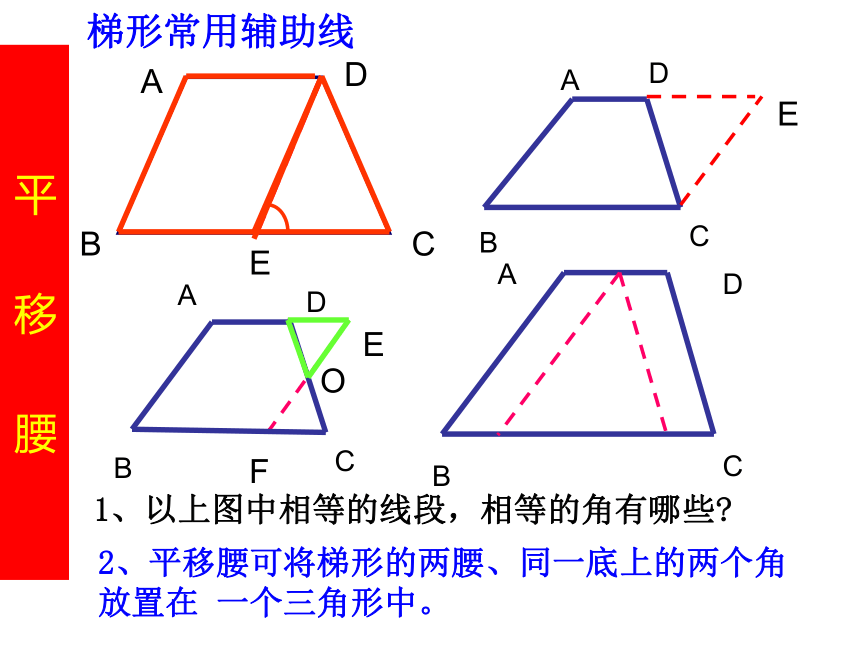
邻角互补44九、几种常见的平行四边形辅助线的画法：1.对角线2.构建新的平行四边形3.构建全等三角形4.构建等腰三角形平 移 腰1、以上图中相等的线段，相等的角有哪些?2、平移腰可将梯形的两腰、同一底上的两个角放置在 一个三角形中。梯形常用辅助线作 高补 三 角 形1、 若梯形ABCD是等腰梯形时，ΔOBC是什么三角形？2、梯形满足什么条件时，ΔOBC是直角三角形？平 移 对 角 线1、当AC⊥BD时，ΔBED是什么三角形？2、当AC=BD时，ΔBED又是什么三角形？3 、ΔBED与梯形ABCD的面积关系如何?其 他 方 法 2.平行四边形的识别方法： （3）∵AD=BC ，AB=DC
∴四边形ABCD是平行四边形 （2）∵AD// BC，AD=BC
∴四边形ABCD是平行四边形 （1）∵AD//BC，AB//CD
∴四边形ABCD是平行四边形
（5）∵OA=OC，0B=0D
∴四边形ABCD是平行四边形
（4）∵∠A=∠C，∠B=∠D
∴四边形ABCD是平行四边形
边的角度角的角度对角线的角度？两组对边分别平行O3、平行四边形的特征： （1）∵四边形ABCD是平行四边形
∴ AD// BC，AB// DC （2）∵四边形ABCD是平行四边形
∴∠ BAD=∠DCB，∠ABC=∠ADC （3）∵四边形ABCD是平行四边形
∴OA=OC，OB=OD 边的角度 角的角度 对角线的角度1、已知：如图，O正方形ABCD的中心，BE平分∠DBC，交DC于点E，延长BC到点F，使CF＝CE，连结DF，交BE的延长线于点G，连结OG．
（1）.求证： OG与BF有什么关系？证明你的结论；
（2）DG＝4－2 ，求：正方形ABCD的面积．解:(1)证△DCF≌ △BCE,得∠CDF= ∠ EBC,可得BG⊥DF,再证△BGF≌ △BGD1、已知：如图，O正方形ABCD的中心，BE平分∠DBC，交DC于点E，延长BC到点F，使CF＝CE，连结DF，交BE的延长线于点G，连结OG．
（1）.求证： OG与BF有什么关系？证明你的结论；
（2）DG＝4－2 ，求：正方形ABCD的面积．解:(2)设BC=x,CF=y.可有x2+y2=(8—4 )2,由BF=BD可得x+y= x注意：运算过程中不要把数据结果算出，到后来可约分。解⑴BE是角平分线（已知）和DG=FG（未知），联想BG⊥DF,故需要证∠FBG=∠FDC（2）设BC=x,CF=y,则有：x2+y2=(8 -- 4 )2,
x+y= x(由BD=BF得来)注意：计算时不能在计算过程中算出结果，保留原有形式可以约分
2．如图，E、F把四边形ABCD的对角线
三等分，DE、DF的延长线分别平分
AB,BC于G,H
求证：四边形ABCD是平行四边形。 D C
E F H
A G B运用中位线定理证明四边形DEBF为平行四边形，从而证出AC和BD互相平分。.3.如图，△ABC中，∠ACB=90°，∠CAD=30°，AC=BC=AD．求证：BD=CD．与第38、39题比较解： 证法一：由300联想定理，构造直角三角形。
如图，过C作CE⊥AD于E，过D作DF⊥BC于F．
∵∠CAD=30°，∴∠ACE=60°，且2CE=AC.
∵AC=AD，∠CAD=30°，∴∠ACD=75°，
∴∠FCD=90°―∠ACD=15°，∠ECD=∠ACD―∠ACE=15°.
∴△CED≌△CFD，
∴2CF=2CE=AC=BC，∴CF=BF．
∴Rt△CDF≌Rt△BDF，
∴BD=CD． 证法二：由等腰直角三角形是正方形的一部分，构造正方形
如图，作正方形AEBC，连结ED．
∵∠BAD=45°―∠CAD=45°―30°=15°
∴∠EAD=∠EAB+∠BAD=60°，
又AD=AC=AE，
∴△ADE是等边三角形，
∴ED=AD=AC=EB，
∴∠DEB=90°―∠AED=30°
∴△ACD≌△EBD，∴CD=BD.3.如图，△ABC中，∠ACB=90°，∠CAD=30°，AC=BC=AD．求证：BD=CD．P解：作正△PCD,可证△PAD ≌ △PAC ≌ △CDB,可证PA=BD,
∠PAD=∠PDA=15°→PA=PD →CD=BD证法三.3.如图，△ABC中，∠ACB=90°，∠CAD=30°，AC=BC=AD．求证：BD=CD．P作△CAD关于AD对称，可证△PAD≌ △CAD, ∠DAB=PAB=15°, △PAC为正三角形，△CDB≌△CDP,BD=PD,CD=BD证法四4、已知：矩形ABCD中，延长BC至E，使BE=BD,F是DE中点，连接AF、CF.
求证：AF⊥CF.QH平行线+中线→构造全等三角形或平行四边形证△ACQ 或△ACH为等腰三角形4、已知：矩形ABCD中，延长BC至E，使BE=BD,F是DE中点，连接AF、CF.
求证：AF⊥CF.联想“三线合一”定理证△ADF≌ △BCF4、已知：矩形ABCD中，延长BC至E，使BE=BD,F是DE中点，连接AF、CF.
求证：AF⊥CF.p运用中位线定理证出PF=AC的一半，可得出结论。5.在正方形ABCD中, M为AB的中点，MN⊥MD，BN平分∠CBE并交MN于N．
试说明：MD=MN．解：AD的中点P，连结PM．从而△MPD≌△NBM，故DM=MN
P6.等腰梯形ABCD中，E为CD的中点，EF⊥AB于F，如果AB=6，EF=5，求梯形ABCD的面积． PQ解：连结AE交BC的延长线于G点，连结BE．先说明△ADE≌△GCE，得到AE=GE， S△ABG=S梯形ABCD=2S△ABE=
2×15=30．7.如图,在□ABCD外有一点E,若AE⊥EC,BE⊥ED.求证：□ABCD是矩形.O证明】连接AC、BD交于点O，连接EO.
∵CDBEAO
四边形ABCD是平行四边形,
∴AO=CO,BO=DO
∵AE⊥EC,
∴∠AEC=90°，∴AC=2EO
又∵BD⊥DE，
∴∠BED=90°，∴BD=2EO
∴AC=BD
∴四边形ABCD是矩形.
8.如图，正方形ABCD中，P是对角线AC上一动点，PE⊥AB，PF⊥BC，垂足分别为E、F小红同学发现：PD⊥EF，且PD=EF，且矩形PEBF的周长不变．不知小红的发现是否正确，请说说你的看法．PFEBACDQ解】小红的发现是正确，其理由如下：
连接BP,延长DP交EF于Q.
（1）∵四边形ABCD是正方形 ∴CB=CD,∠BCP=∠DCP=45°
∴△BCP≌△DCP，∴PD=PB 又∵PE⊥AB，PF⊥BC， ∴∠BEP=∠BFP=∠EBF=90°，∴四边形BEPF是矩形 ∴PB=EF,∴PD=EF
（2）∵PE⊥AB，PF⊥BC，∴△AEP和△CFP均为等腰直角三角形
∴AE=PE,CF=PF
∴矩形PEBF的周长=AB+BC=2AB（为定值）
（3）∵PF∥CD，∴∠FPQ=∠PDC ∵△BCP≌△DCP，∴∠PDC=∠PBF
∵四边形PEBF是矩形,∴∠PBF=∠PEF ∴∠PEF=∠FPQ
又∵∠PEF+∠PFE=90°，∴∠FPQ+∠PFE=90°
∴∠PQF=90°，∴PD⊥EF.
【另证】延长EP交CD于点R,则CFPR为正方形
∴可证△PEF≌△RDF
∴∠PEF=∠PDR 又∵∠DPR=∠EPQ 而∠PDR+∠DPR=90°，∴∠PEF+∠EPQ=90° ∴∠EQP=90°，∴PD⊥EF.
注意：延长FP交AD于点G,也可证
方法一8.如图，正方形ABCD中，P是对角线AC上一动点，PE⊥AB，PF⊥BC，垂足分别为E、F小红同学发现：PD⊥EF，且PD=EF，且矩形PEBF的周长不变．不知小红的发现是否正确，请说说你的看法．PFEBACDQRG9. 如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=2DC,对角线AC⊥BD,垂足为F,过点F作EF∥AB,交AD于点E,CF=4cm.
⑴求证：四边形ABFE是等腰梯形;
⑵求AE的长.G解（1）AB=2CD=2BG→DG是AB的中垂线→DA=DB →∠DAB=∠DBA
（2）利用△ABC为射影图可作10. 如图，等腰梯形ABCD中，AD∥BC，AB=DC，AC⊥BD
若AD=3，BC=7，求梯形ABCD的面积；EF11.已知正方形ABCD的边长为1，G是AB边上任意一点，以BG为一边作如图所示的正方形GBEF，连结AC，FC。则△ＡＣＦ的面积等于多少？ BF∥AC, 可得：S△AFC=S△ABC=0.512．在菱形ABCD中，∠ADC=60°，AD=2，E是AD中点，P是对角线BD上的一个动点。
⑴试探求PA+PE的值是否是一个定值。
解：不是定值
⑵如果不是，试求出它的最小值（只要写出结果，并在图中画出PA+PE的值最小时的P点位置）
解：PA+PE的最小值为，连结CE交BO于P，点P为所求。A13．（湖州05年中考选做题）如图，四边形ABCD和BEFG均为正方形，求ABCDGEFQ解：作DP∥AG， DP=AG连结PF，延长GF交直线BC于Q
∴四边形AGPD为平行四边形PG=AD=AB，PG∥AD∥BC ∴∠PGQ=∠BQG
又∵GQ∥BE ∴∠GQB=∠CBE
∴∠CBE=∠PGQ
又∵∠ABG+∠GBC=90° ∠CBE+∠GBC=90°∴∠ABG=∠CBE
∴∠PGQ=∠ABG
又∵BG=GF
P∴△ABG≌△PGF
∴AG=PF ∠BAG=∠FPG
从而可证△PDF为等腰直角三角形
13．（湖州05年中考选做题）如图，四边形ABCD和BEFG均为正方形，求ABCDGEF 解：平移△ABG到CD， 连结PF，PG,CE
∴四边形AGPD,ECPF,BCPG为平行四边形∴△ABG≌△BCE≌△PGF ≌△PGF
∴PD=PF
∵ ∠BEC= ∠DPC
∠FEC= ∠FPC
∴ ∠DPF= ∠BEF=90°
P13．（湖州05年中考选做题）如图，四边形ABCD和BEFG均为正方形，求ABCDGEF解：作AP∥DF， DP=AG连结PF，PG
∴四边形APFD为平行四边形PF=AD=AB，PF∥AD∥BC ,BH
∥FR
∴四边形BRFH为平行四边形
∴∠GBC=∠HFR
∴∠ABG=∠GFH ∴△ABG≌△PGF
∴AG=PG, ∠AGB=∠PGF
∴∠AGB=∠BGF= 90°
从而可证△AGP为等腰直角三角形
PHR14．如图，在以点O为原点的直角坐标系中，点A的坐标为（0，1），直线x=1交x轴于点B，点P为线段AB上的一动点，作直线PC⊥PO，交直线x=1于点C，过点P作直线MN平行于x轴，交y轴于点M，交直线x=1于点N。⑴当点C在第一象限时，求证△OPM≌△PCN
⑵当点C在第一象限时，设PA=m，四边形POBC的面积为S，请求出S与m之间的函数关系式，并写出自变量m的取值范围。
⑶当P在线段AB上移动时，点C随之在直线x=1上移动，△PBC能否成为等腰三角形？如果能，求出点P的坐标；如果不能，请说明理由。解：⑴利用45°角，可证PN=NB=OM 从而证出△OPM≌△PCNS=SOMNB-2S△POM即 （0≤m＜）（2）⑶①当P与A重合时，PC=BC=OA=1 ∴P（0，1）
②当C在第一象限时，∠PCB>90°

当PC2=BC2时，即 解得 m1=0 m2=m=0时即 P与A重合
m= 不满足0≤m＜


舍去③当P在第四象限时，∠PBC>90°只有PB=CB方法一：PM=CN= BN=PN=1-PB=NB=-m方法二：证明AO=AP更简结，∠APO+ ∠B PC= ∠AOP+ ∠POB=90°→ ∠APO= ∠AOP →AO=AP
综上述，P（0，1）或（解得：m=115．已知正方形ABCD的面积为35cm2,E、F分别为边AB、BC上的点，AF和CE相交于点G，并且△ABF的面积为5cm2，△BCE的面积为14cm2，求四边形BEGF的面积。 ABCDFEMmnpq解：连结AC、BG
∵m+n+p=14 p+Q+n=5
解得n= Q= p=∴SBEGF=p+n== 16．已知P是矩形ABCD内一点，如果PA=3，PB=4，PC=5，求PD的长度。PEFMNxxxyyymmmnnnX2+m2=25……① m2+n2=16……②
Y2+n2=9……③ x2+y2=PD2……④由①+③-—②可得：
x2+y2=PD2=1817，在矩形ABCD中，已知AB=4，BC=8，P、Q分别是BC、CD上的点， ，E、F、G分别为PA、PQ、PC的中点。求四边形EPGF的面积。M解：取BP中点M，连结EM , 设FG=a
则CQ=2a. PM=2a
GM=4
SEPGF=SEFGM-S△EMP

=
= 2a+4—2a
=418.一张重要文件被切割成一些小碎片，每块碎片都是凸多边形，将其重新粘合成原形后，有交结点30个，其中20个点在原矩形的周界上（包括原矩形的四个顶点），其余10个点在矩形内部，在矩形内部有45条粘缝（两个结点之间的线段算是一条粘缝，如图示）。试求该张重要文件所破碎裂成的各种类型（指三角形、四边形、五边形等）的块数。（说明：若凸多边形的周界边上有n个点，就将其看成n边形，如图中的多边形ABCDE要看成五边形）解：设全部碎片中共有三角形a3个，四边形a4个……k边形ak 个（a3,a4,……ak为非负整数）
第一步：从内角考虑，
180°a3+360°a4+……（k-2）180°×ak=10×360°+ 180°×16+360°内部10个点形成10个周角
除4个顶点外，16个角都是平角四个直角顶点之和第二步：从边考虑，
3a3+4a4+……+kak=2×45+20=110…………② ∴a3+2a4+……+（k—2）ak=38…………①内部45条粘缝算了两次矩形周界上有20个点，有20条边第三步：②-①可得
2a3+2a4+……+2ak=110-38=72
即：a3+a4+……+ak=36…………③
①-③可得
a4+2a5+3a6+……+（k-3）ak=2…………④
第四步：由④可得 a6=a7=a8=……ak=0
（ ∵a6有一个，就大于2……）
∴a4+2a5=2
∴a4=2 a5=0
a4=0 a5=1
由③可知，碎片共有36块
∴三角形有34块，四边形有2块
或三角形有35块，五边形有1块19．在直角坐标系中，直线 分别交x轴、y轴于C、A两点，将射线AM绕着点A顺时针旋转45°得到射线AN，点D为AM上的动点，点B为AN上的动点，点C在∠MAN内部。
⑴求线段AC的长。
⑵当AM∥x轴，且四边形ABCD为梯形时，求△BCD的面积。
⑶求△BCD周长的最小值。
⑷当△BCD的周长取得最小值，且BD= ，求△BCD的面积。：⑴A（0,2） C(⑵①当AD∥BC时，
∠ABO=∠MAN=45°
∴OB=OA=2
∴BC=∴S△BCD=②当AB∥CD时，四边形AECD为平行四边形
∴S△ACD= S△BCD=OE=OA=2
∴EC=CO-OE=∴S△ACD==综合上述可得，S△BCD=,0) ∴AC=4MNC1C2DB⑶作C关于AM的对称点C1，作C关于AN的对称点C2，连结C1C2分别交AM、
AN于D、B，则C1C2=C△BCD 由对称关系可知 ∠CAC2=2∠MAN=90°
AC1=AC2=AC=4 在RT△C1AC2中可得，C1C2=⑷由⑶可知，△ADC1≌△ADC△ABC2≌△ABC∴∠BCD=∠ACD+∠ACB=45°+45°=90 设BC=a,CD=b由⑶可得 由勾股定理可得
由①2-②可得 ∴ 2ab= ab=S△BCD=……①……②20.（福建中考）在梯形ABCD中，M、N是两底CD、AB的中点，连接MN,求MN与两腰AD,BC的数量关系E2MN＜ AD+BC21.梯形ABCD中，AB//CD，M、N分别是CD、AB的中点，∠A+∠B=900.求证：MN= （AB-CD）EF22.在六边形ABCDEF中，六个内角都是1200，其连续四边长依次是1、9、9、5厘米，求六边形的周长？ ABCDDEF GHI1995※.(北京竞赛)已知:六边形ABCDEF中, ∠A=∠B=∠C=∠D=∠E=∠F,且AB+BC=11,
FA-CD=3.求BC+DE的长.RPABCDEFQ解1：如图，将六边形ABCDEF的三边AB，CD，EF双向延长，得⊿PQR∵六边 形内角和是720°
∴∠A=∠B=∠C=∠D=∠E=∠F=120°
∴该六边形各外角均为60°
故 ⊿PQR，⊿PCB，⊿DQE，⊿FRA均为等边三角形
∴BC+DE=PQ-CD=PR-CD=FA+AB+BC-CD
=（AB+BC）+（FA-CD）=11+3=14。解2：如图，延长FA，CB交于P，延长FE，CD交于Q，易证四边形FPCQ是平行四边形，⊿ABP和⊿DEQ均是等边三角形。
∵PF=CQ，∴FA+AB=DE+CD
∴DE-AB=FA-CD=3 ①
又 AB+BC=11 ②
①+② 得，DE+BC=3+11=14。FEQAPBCD FEABCDQP还有其它的解法吗？问：如图，若补成等腰梯形来解，
你想试一试吗？23. 如图在四边形ABCD中，AB⊥BC, AD⊥CD, ∠A=1350,BC=6,AD=2 .求四边形ABCD的面积？ABCDE24.如图，在矩形ABCD中，E、F分别是边DC、AD上的点，且EF=EB.EF⊥EB。
求证:AE平分∠BAD?ABCDEFM25.如图甲，在△ABC中，∠ACB为锐角，点D为射线BC上一动点，连接AD，从AD的右侧作正方形ADEF.
(1)如果AB=AC，∠BAC=900,解答下列问题。
①当D在线段BC上时，（与点B不重合）如图乙，线段CF、BD之间的位置关系式________数量关系是_________。垂直CF=BDABDCF25.如图甲，在△ABC中，∠ACB为锐角，点D为射线BC上一动点，连接AD，从AD的右侧作正方形ADEF.
(1)如果AB=AC，∠BAC=900,解答下列问题②当点D在线段BC的延长线上时，如图丙，①中结论是否仍然成立，试说明理由？ABCDEF证明△DAB≌△FAC25.如图甲，在△ABC中，∠ACB为锐角，点D为射线BC上一动点，连接AD，从AD的右侧作正方形ADEF.
（2）如果AB≠AC, ∠BAC≠900.点D在线段BC上运动，试探究。当△ABC满足一个什么条件时，CF⊥BC.(点C、F重合除外)画出相应图形，并说明理由。
ABCDEFG过A作AG⊥AC
证明△AGD≌△AFC
得AG=AC,
故∠ACB=45°26.如图，延长四边形ABCD的边AD，BC相交于E，设H、G分别是BD和AC的中点。求
△EHG的面积与四边形ABCD的面积之比?ABCDEGH S△EGH= S△EAH- S△AGH-S△AGE
= S△ABE--- S△ACH---- S△ACE

= （S△ABE--- S△ACH--- S△ACE）

= （Ｓ△ＡＢＨ＋Ｓ△BCH）＝　　　ＳＡＢＣＤ27.在梯形ABCD中，AB//CD，对角线AC,BD交于点O,三角形COD的面积为S1,三角形AOD的面积为S2,三角形AOB的面积为S3, 三角形BOC的面积为S4.求证:S1×S4=S2×S3ABCDOS1S2S3S428. 四边形ABCD中,对角线AC,BD交于点O,
三角形COD的面积为S1,三角形AOD的面积为S2,
三角形AOB的面积为S3, 三角形BOC的面积为S4.
求证:S1×S4=S2×S3ＢＣＤＡＯＳ１Ｓ２Ｓ３Ｓ４29.四边形ABCD中,点O为对角线AC上任意一点，
连接OD,OB,三角形COD的面积为S1,
三角形AOD的面积为S2,三角形AOB的面积为S3,
三角形BOC的面积为S4.求证:S1×S4=S2×S3ＡＢＣＤＯＳ１Ｓ２Ｓ３Ｓ４30.如图，已知矩形ABCD中，AB=3,BC=8,E是BC中点。
DM⊥AE于M。求DM的长？
ＡＢＣＤＥＭ解：AE=5,S△ADE=3×8÷2=12
DM=2S△ADE÷AE=4.831.如图。正方形ABCD中，∠EBF=450,MB⊥EF与M.
求证：AB=BM
ABCDEFMN解：把△BCF绕点B逆时针旋转90°到△ABN。
证△BEN≌△BEF,由全等三角形的对应高相等可得AB=BM32.正方形ABCD的边长为1，P是BC上一点，
直线PD交AB的延长线于点Q，若PD=PB+BQ,求PD?
ABCDPQT解：作BT=PB→AT=PC→△DAT≌△DCP→DT=DP=TQ→∠CDP=∠PDB=∠ADT=30°,可得PD33.如图，在梯形ABCD的中，AB//CD,且AB=2CD,M、N分别
是对角线AC、BD的中点。设梯形ABCD的周长为a，
四边形CDMN的周长为b，求a与b的关系？
ABCDMNPQR解：延长后可得2PM=2NQ=2MN=CD=AR=BR,四边形BCDR、DMQC、DPNC都是平行四边形，P,M,N,Q,R都是中点，设MN=m,则可得a=2b34.在直角△ABC中，∠BAC=900,AB>AC,
分别以其直角边AB和斜边BC为边做正方形
ABDE和BCFG，使得△ABC落在这两个正方形内部，求证：AG⊥CD
BCDEAGF解; ∠ABG=∠DBC,BG=BC,AB=BD→△ABG≌△DBCH→∠BAG=∠BDC,且∠BAG+∠CAH=90°, ∠BDC+∠CDE=90°,可证∠CAH=∠CDE
35.如图，正方形ABCD中，E为CD中点，F为BC上一点，∠FAE=∠DAE,求证：AF=AD+CFBACDEFG作EG⊥AF→△ADE≌△AGE→DE=EG=CE→△EGF≌△ECF→CF=GF
35.如图，正方形ABCD中，E为CD中点，F为BC上一点，∠FAE=∠DAE,求证：AF=AD+CFQ36. 如图，正方形ABCD中，点E,F分别在BC,
CD上，AF平分∠DAE.求证：AE=BE+DF
分析：作△ADF≌△ABG→∠DAF=BAG→
∠GAF=90°→∠G=∠GAE→AE=EG→
AE=BE+DF
FBCDAEG37.在正方形ABCD中，E是CD的中点，P在BC上，且AP=PC+CD，
求证：AE平分∠DAP。 Q37.解：延长AE交BC的延长线于Q．因为四边
形ABCD是正方形，所以AD=CD，AD∥BQ．又E是CD的中点．因此，△ADE与△ECQ关于点E成中心对称．则有AD＝CQ，∠DAE＝∠EQC．又因为AP＝PC＋CD，所以AP＝PC＋CQ，于是∠PAE＝∠Q． 故∠DAE＝∠PAE，即有AE平分∠DAP．
38.如图，P是正方形ABCD内一点，∠PAD=∠PDA=15°，求证：△PBC为正三角形。
分析：把△APD绕点D沿逆时针方向旋转90°到△DCP1，把△DCP1沿CD作轴对称△DCP2
可得△PDP2为正三角形→∠PP2C=360°-60°-150°=150°→∠PP2C=∠DP2C→△PP2C≌△DP2C→PC=CD或∠PCB=60°
P1P2ABCDP与第3、39题比较39.如图，在直角三角形ABC中，∠BAC=90°，AC=AB,D为△ABC内一点，且
∠DAC=∠DCA=15°,求证：AB=BD
分析：把△ACD绕点A沿逆时针方向旋转90°到△ABE的位置，把△AEB沿AB作轴对称得到△AFB→△ADF为正三角形。
ACBDEF与第38、3题比较40. 如图，在平行四边形ABCD中，E为CD边中点，PA⊥BE于P，求证：DA=DP。
分析：延长BE,AD交于F, △BCE≌△DEF→DF=BC→AD=DF→DP为直角三角形APF斜边上的中线→DA=DP ABCDPEF41.如图，在梯形ABCD中,AD∥BC, ∠ABC=90°,AB=BC=2AD,点P是梯形内任意一点，且PA=1,PB=2,PC=3,求梯形ABCD的面积。
分析：作△APB≌△BCQ→∠BPQ=∠BQP=45°和PQ的长→△PQC为直角三角形→∠APB=∠BQC=135°→A,P,Q三点共线
过C作CM⊥BQ于M→在△CMQ中可求CM和QM的值（CM=QM）→在△CMB中可求CB2的值。
ABCDPQM42.正方形ABCD的对角线AC,BD交于点O，DE平分∠ADB交AC于N，求证：BE=2ON.ABCDOENP作DE的中点P,连接OP→BE=2OP,再证∠OPN=∠OMP(利用外角)43.已知E是矩形ABCD的边CB延长线上一点，CE=CA,F是AE中点，求证：BF⊥FD
分析：隐含一个常见的基本图形：夹在平行线间线段的中点。常见方法是以这个点为中心作中心对称变换。ABCDEF同第四题44. 正方形ABCD内有一点P,且PD:PA:PB=1:2：3求：∠APD的度数
解：将△ABP绕点A沿逆时针方向旋转900成△ADE,连接PE.ABCDPE45.在四边形ABCD中，AD=CD,∠ADC=∠B=900，DE⊥AB于E,若四边形ABCD的面积为16，求DE的长。
解：将△ADE绕点D沿逆时针方向旋转900到△DCF的位置，则DF=DE,证出DEBF为正方形，故DE=4ABCDEF46、正方形ABCD所在的平面上找一点P，连接PA,PB,PC,PD,使△PAB, △PBC, △PCD, △PAD都为等腰三角形，平面内符合条件的点有多少个？
分析：两边的中垂线的交点1个
以四个顶点为圆心，半径为正方形边长的圆与中垂线交点8个
共9个47、等边三角形ABC所在的平面上找一点P,使△PAB, △PBC, △PAC为等腰三角形，平面内符合条件的点有多少个？
分析：中垂线的交点1个
以三个顶点为圆心，半径为三角形边长的圆与中垂线交点9个
共10个48、A,B是平面内的两个定点，在平面内找一点C，使△ABC等腰直角三角形，平面内符合条件的点C有多少个？
分析：以AB为腰的有4个
以AB为斜边的有2个
共6个49.E是CD上一点，AE=CD+CE，F是CD的中点。求证；∠BAE=2∠BAF解：作AG平分∠BAE,GH⊥AE可证ABCDFEHG50．分别以△ABC的边AB,AC为边向△ABC外作正方形ABDE和正方形ACFM.求证：△AME的中线AN与△ABC的高线AG位于同一直线。ABCGDEMFQNP分析：先确定AG为高线，延长GA交EM于N,再证AN为
中线。即证△MPA≌△AGC, △EQA≌△AGB,从而可证AG=PM=EQ方法一50．分别以△ABC的边AB,AC为边向△ABC外作正方形ABDE和正方形ACFM.求证：△AME的中线AN与△ABC的高线AG位于同一直线。ABCGDEMFNP分析：先确定N是EM中点，AG是高线，把△AEM绕点A顺时针旋转90°到△AE1C,可证B,A,E1三点共线→A是BE1中点→AN1是△BE1C的中位线→,AN1∥BC,且AG ⊥BC → AN1∥AG,且AN⊥AN1→ N,A,G三点共线方法二N1E151.如图，A为线段BC外一动点，以AB,AC为边向外侧作正方形ABDE和正方形ACFM,不论A的位置在BC同侧如何变化。求证：（1）D,F到直线BC的距离之和为定值。（2）线段DF的中点为定点。ABCDEFMD1F1A1PP1（1）作AA1⊥BC,可证DD1=BA1,FF1=A1C（2）取DF中点为P作PP1⊥BC→PP1为梯形DD1F1F的中位线→
BC=DD1+FF1=2PP1→P为以BC为斜边的等腰直角三角形的直角顶点（定点）52、如图，在直角梯形ABCD中，AD//BC,∠B=900 ,BC=CD且AD>BC,
（1）试以DC所在直线为对称轴，画出梯形ABCD的对称图形A1B1CD,并判断三条直线AB,A1B1、CD是否经过同一个点（记作O）
（2）在(1)问中，设BB1与直线CD交于点E，试说明E是△AA1O的内切圆圆心。ABDCB1A1O解（1）方法一：设直线AB与直线DC交于点O，直线A1B1与直线DC交于点O1。
∵∠OCB=∠O1CB1,BC=B1C, ∠OBC=∠O1B1C=90°,
∴△OCB≌△O1CB1
∴OC=O1C, ∴C与C1重合
∴AB,A1B1,CD经过同一个点O(O1)方法二：可利用相似做52、如图，在直角梯形ABCD中，AD//BC,∠B=900 ,BC=CD且AD>BC,
（1）试以DC所在直线为对称轴，画出梯形ABCD的对称图形A1B1CD,并判断三条直线AB,A1B1、CD是否经过同一个点（记作O）
（2）在(1)问中，设BB1与直线CD交于点E，试说明E是△AA1O的内切圆圆心。ABDCB1A1O解：连接AE,BD, ∵ AD//BC, ∴∠CBD= ∠ADB, ∵BC=CD, ∴∠CBD= ∠CDB, ∴∠CDB= ∠ADB且∠BAD=∠BED=90°,BD=BD
∴△BAD≌ △BED, ∴BA=BE
∴ ∠BAE= ∠BEA, ∵BE∥AA1
∴ ∠EAA1= ∠BEA, ∴ ∠EAA1= ∠BAE,
∵由（1）得∠AOE= ∠EOB1,
∴E是△AA1O的内切圆圆心。
(O1)E53.如图，□ABCD中，EF//BC，GH//AB，EF，
GH的交点P在BD上，图中面积相等的四边形
有_________对F54.已知梯形上、下底的长分别为6、8，一腰长为7，则另一个腰a的范围是( )
5＜a＜9
55.　如图1-4，□ABCD中，BE、DF分别平分∠ABD、∠CDB，DC=DB。求证：DE=CF。证明：△ABE≌△DBE→AE=DE
△ABE≌△CDF→AE=CF
DE=CF
54.如图E、F分别为AC、BD的中点，
，E、F不都是对角线交点。
求证：2EF>CD－AB
ABCDG56.有7×6的方格纸型的棋盘，以棋盘上竖线和横线为边，以棋盘中各交叉点为顶点的正方形有 ___个.你愿意把得到上述结论的探究方法与他人交流吗？在小组中选一个代表简要的讲出你们的探究过程。112BxyCAD57、如图，在第一象限内找一点D，使四边形ABCD是平行四边形，那么点D的坐标是 . （2，2）如图，在直角坐标系内找一点D，使四边形ABCD是平行四边形，那么点D的坐标是 . （-4，2）（2，-2）（2，2）2.如图(2),若AB与CD不平行时,(1)式是否成立?3.如图(3),若AB与CD相交于点O时,问S△DMC与S△DAC、S△DBC有何种相等关系?试证明你的结论.58．如图（１）AB,CD是两条线段,M是AB的中点,S△DMC, S△DAC和S△DBC分别表示△DMC, △DAC, △DBC的面积.
1.当AB∥CD时,证明S△DMC =　 (S△DAC +S△DBC).解（3）2S△DMC=S△DBC -—S△DAC59、如图，AB⊥BC，DC⊥BC，垂足分别为B，C. 当AB=4,DC=1,BC=4时，在线段BC上是否存在点P，使AP⊥PD？如果存在，求出线段BP的长；如果不存在，请说明理由；
设AB=a，DC=b，BC=c,那么当a，b，c之间满足什么关系时，在直线BC上存在点P，使AP⊥PD?