1.1锐角三角形(1)

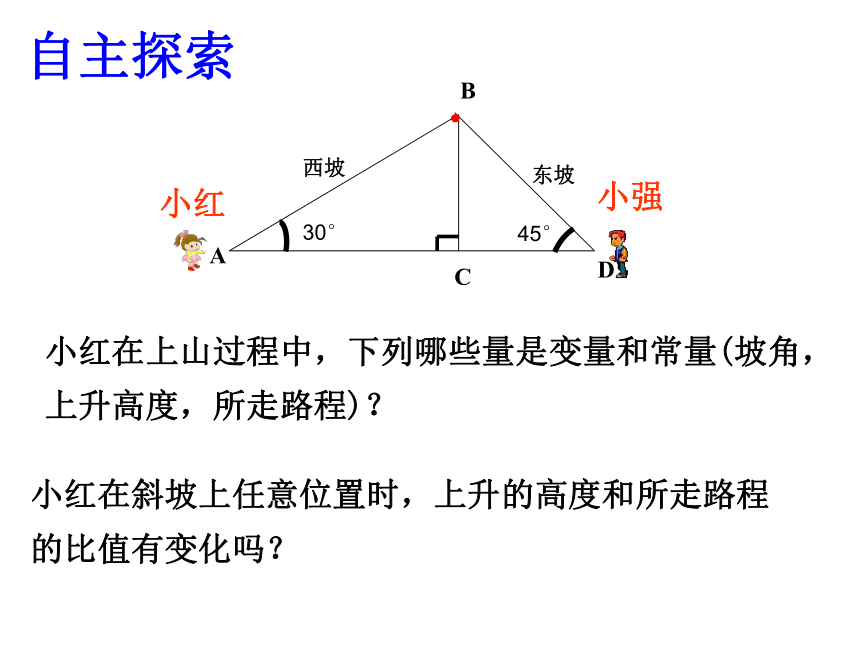
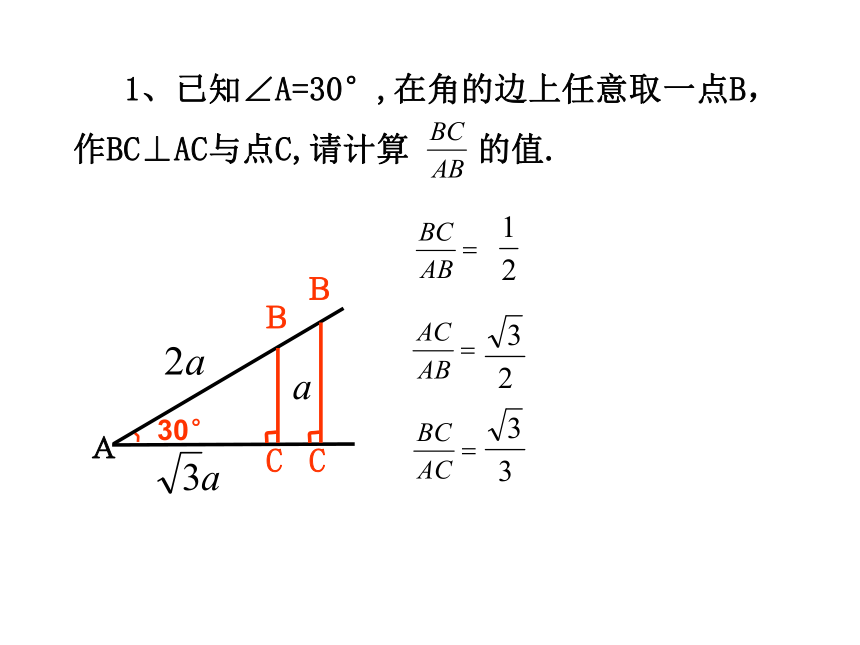
课件19张PPT。1.1锐角三角函数(1)小红出发地小强出发地情景引入 AB C D西坡东坡小红小强小红在上山过程中，下列哪些量是变量和常量(坡角，上升高度，所走路程)？自主探索小红在斜坡上任意位置时，上升的高度和所走路程的比值有变化吗？30°45° 1、已知∠A=30°,在角的边上任意取一点B，
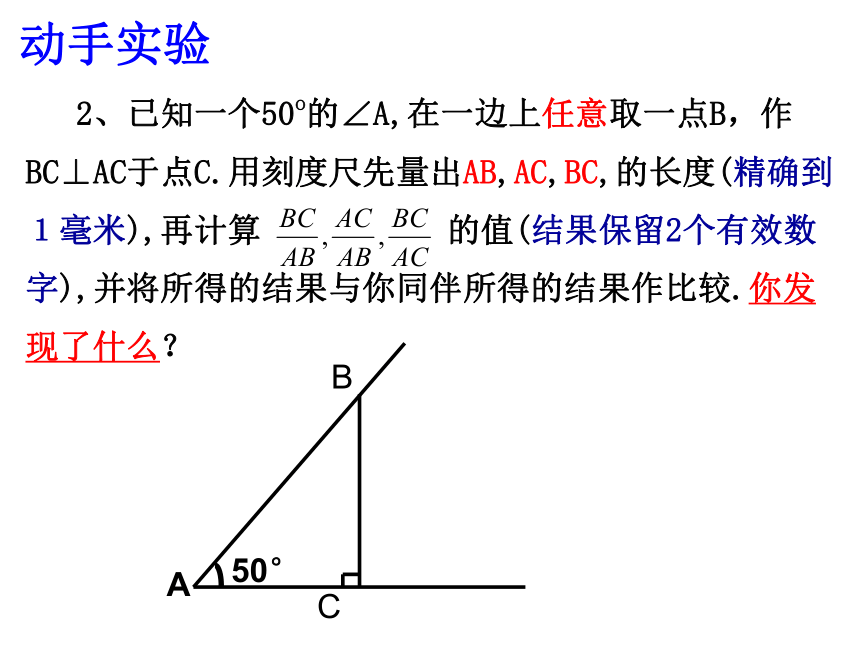
作BC⊥AC与点C,请计算 的值. 动手实验 2、已知一个50o的∠A,在一边上任意取一点B，作BC⊥AC于点C.用刻度尺先量出AB,AC,BC,的长度(精确到１毫米),再计算 的值(结果保留2个有效数字),并将所得的结果与你同伴所得的结果作比较.你发现了什么？50°BC寻找规律角度不变，比值不变
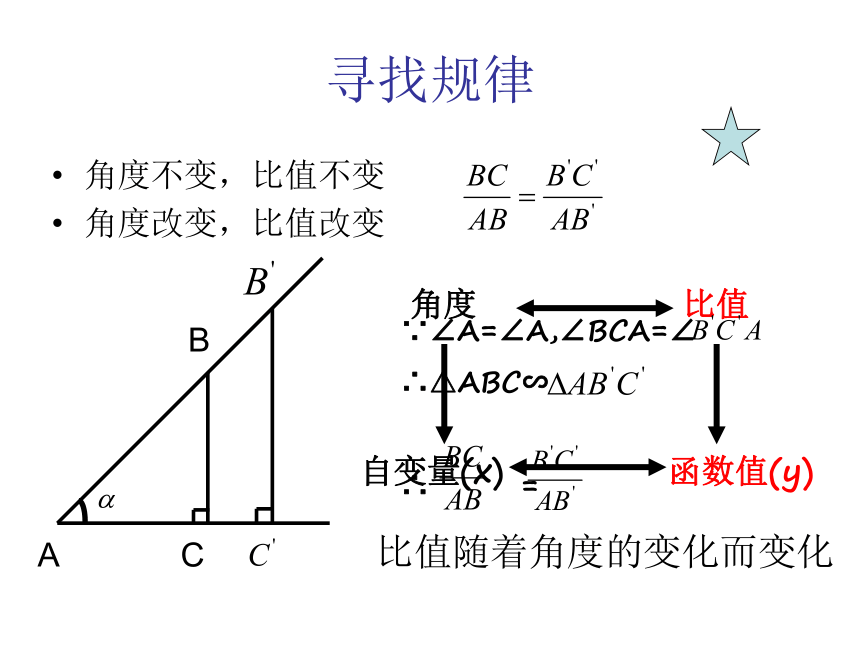
角度改变，比值改变 比值随着角度的变化而变化 ∵∠A=∠A,∠BCA=∠
∴△ABC∽
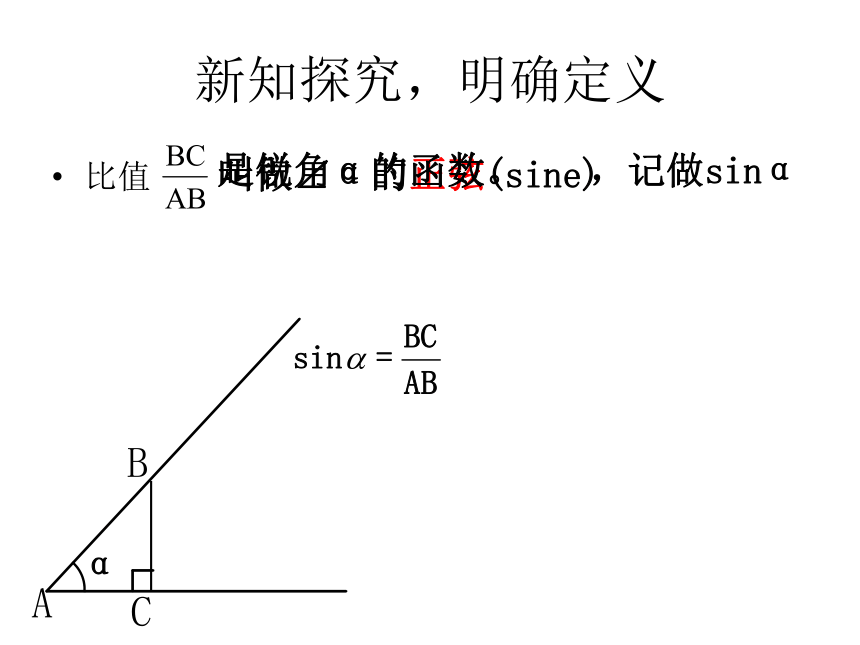
∴ = ACB新知探究，明确定义 比值叫做∠α的正弦(sine)是锐角α的函数。，记做sinαAα BC
比值
比值新知探究，明确定义比值A BC 叫做∠α的余弦(cosine)，记做cosα叫做∠α的正切(tangent)，记做tanα锐角α的正弦、余弦、正切
统称为∠α的三角函数 叫做∠α的正弦(sine)，记做sinα新知探究，明确定义如图，在Rt△ABC中，∠C=Rt∠ ∠A
的
对
边∠A的邻边斜边练习拓展，层层递进例1.在Rt⊿ABC中，∠C=Rt∠，AB=5，BC=3，求锐角∠A的正弦、余弦、正切.变式1
在Rt⊿ABC中，∠C=Rt∠，AC：BC=1：2，求锐角∠B的各三角函数的值.解：设AC=k，BC=2k，得AB=变式2在Rt⊿ABC中，∠C=Rt∠，
求锐角∠A的余弦 .例1.在Rt△ABC中，∠C=Rt∠，AB=5，BC=3，求锐角∠A的正弦、余弦、正切。ABC观察表中的计算结果，你发现了什么？请说明理由.如图:在等腰△ABC中,AB=AC=5,BC=6.则下列结论正确的是（ ） B．sinB= C.以上结论都不正确
C选一选：A．sinB=提示:过点A作AD垂直于BC于D.小明在解决某一数学问题时，算得 ，你觉得他算对吗？为什么？想一想：0< <10< <1反馈练习： 根据本节“合作学习”中的第1题探索 结果，说出30°角的正弦、余弦、正切的值.探索45°，60°的正弦、余弦、正切的值.拓展探索：如图，一根3m长的竹竿AB斜靠在墙上，当端点A离地面的高度AC长为1m时，竹竿AB的倾斜角α的正切tanα的值是多少？当端点A位于D，离地面的高度CD为2m时，倾斜角β的正切tanβ的值是多少？tanα的值可以大于100吗？请求出锐角α的正切函数的范围。归纳小结，反思提高sinAcosAtanA∠A的正弦∠A的余弦∠A的正切00我来说作业：1、完成数学作业本。
2、课本P6：A组。