2.3一元二次方程的应用（第一课时）

课件13张PPT。2.3一元二次方程的应用①在一次义卖活动中，某同学带上家中
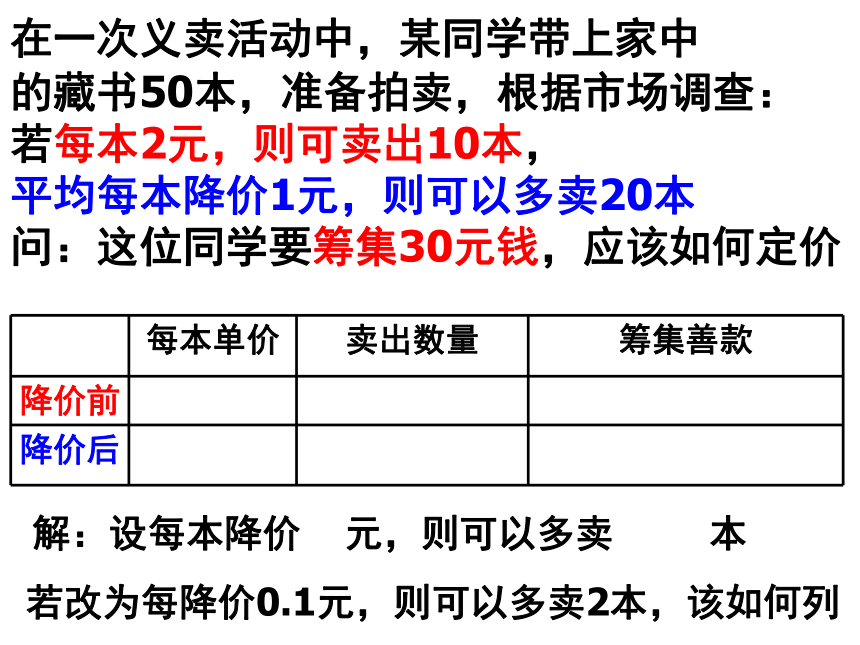
的藏书50本，准备拍卖，根据市场调查：
若每本2元，则可卖出10本，
平均每本降价1元，则可以多卖20本
问：这位同学要筹集30元钱，应该如何定价解：设每本降价 x 元，则可以多卖 20x 本 若改为每降价0.1元，则可以多卖2本，该如何列 某花圃用花盆培育某种花苗,经过实验发现
每盆的盈利与每盆的株数构成一定的关系.
每盆植入3株时,平均单株盈利3元;
以同样的栽培条件,若每盆每增加1株,
平均单株盈利就减少0.5元.
要使每盆的盈利达到10元,
每盆应该植多少株? 例11.义卖现场A同学看准商机，果断买下一个3元的u盘，加价x%，则卖价为 ,
B同学买下后，再加价x%，
则卖价为 ,3(1+x%)2 倒卖问题3(1+x%) 二次增长后的值为设基数为a，平均增长率为x，
则一次增长后的值为增长率问题 问题:截止到2000年12月31日，我国的上网计算机总数为892万台；截止到2002年12月31日，我国的上网计算机总数已达2083万台.
（1）求2000年12月31日至2002年12月31日我国的上网计算机台数的年平均增长率（精确到0.1%）. 基数×(1＋增长率)2 =新数 例2问题: （2）上网计算机总数2001年12月31日至2003年12月31日的年平均增长率与2000年12月31日至2002年12月31日的年平均增长率相比，哪段时间年平均增长率较大？基数×(1＋增长率)2 =新数 1、2次增长、降低率问题的有关公式 ：
原有量╳(1+增加的百分数)2 =后来的量
原有量╳(1-减少的百分数)2 =后来的量
2、解这类问题的方程，用直接开平方法做简便。 知识点导学： 2.某校坚持对学生进行近视眼的防治,近视学生人数逐年减少.据统计,今年的近视学生人数是前年人数的75℅,那么这两年平均每年近视学生人数降低的百分率是多少(精确到1℅)?课内练习(1-x)2=0.75 提示：增长率问题中若基数不明确，
通常设为“1”,或设为a等设为“1”更常用. 已知两个连续正奇数的积等于63,求这两个数.课内练习 经检验,x1=7,x2=－9,是方程的解,
但x2=－9不合题意,舍去 道路设计：40m26mxx144m2??道路设计：40m26mxx144m2??1.某市进行环境绿化，计划两年内把绿化
面积增加44%，问平均每年增长的百分率是多少？2.某公司计划经过两年把某种商品的生产成本降低19%，那么平均每年需降低百分之几? 某商厦今年一月份销售额为60万元，二月份由于某种原因，销售额下降了10%，以后改进管理，大大激发了全体员工的积极性，月销售额大幅上升，到四月份销售额猛增到96万元，求三、四月份平均每月增长的百分率是多少？（精确到0.1%） 解：设三、四月份平均每月增长率为x，依题意，得： 60（1-10%）（1+x）2=96 解得： 由于增长率不能为负数，故 不合题意，舍去。 所以 答（略）实践与应用：