1.1认识三角形

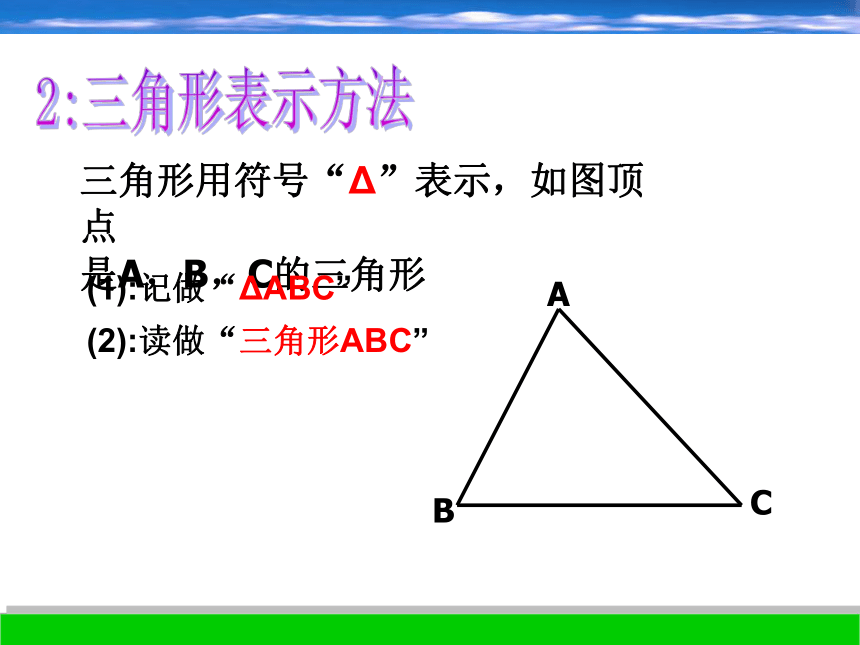
课件20张PPT。1.1　三角形那么,怎样的图形叫做三角形呢?1:三角形定义:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形ABC三角形用符号“Δ”表示，如图顶点
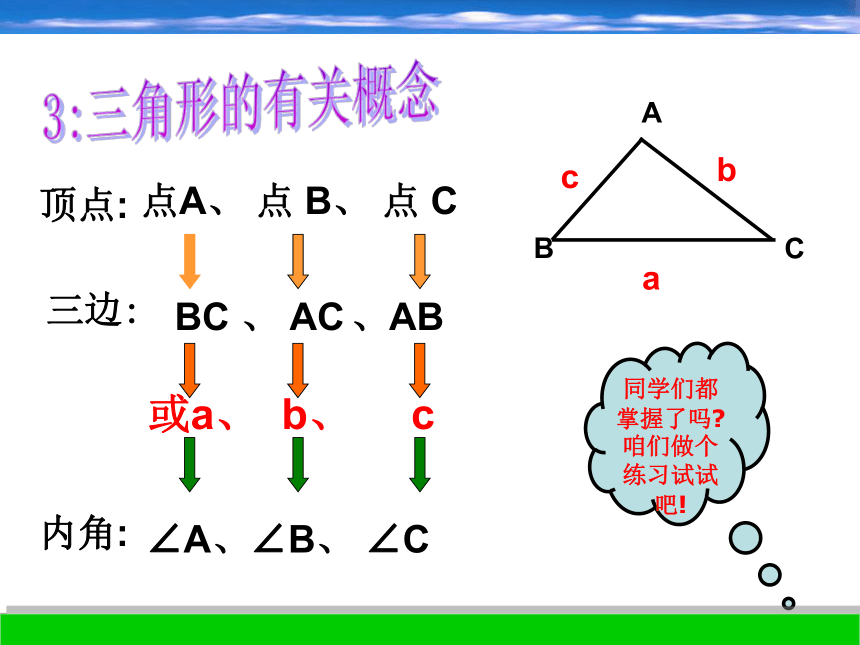
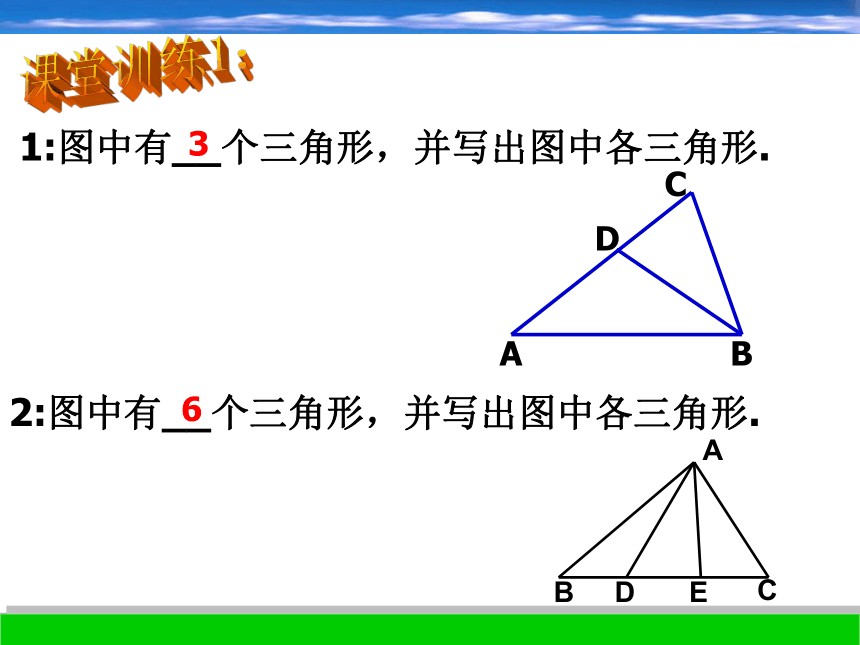
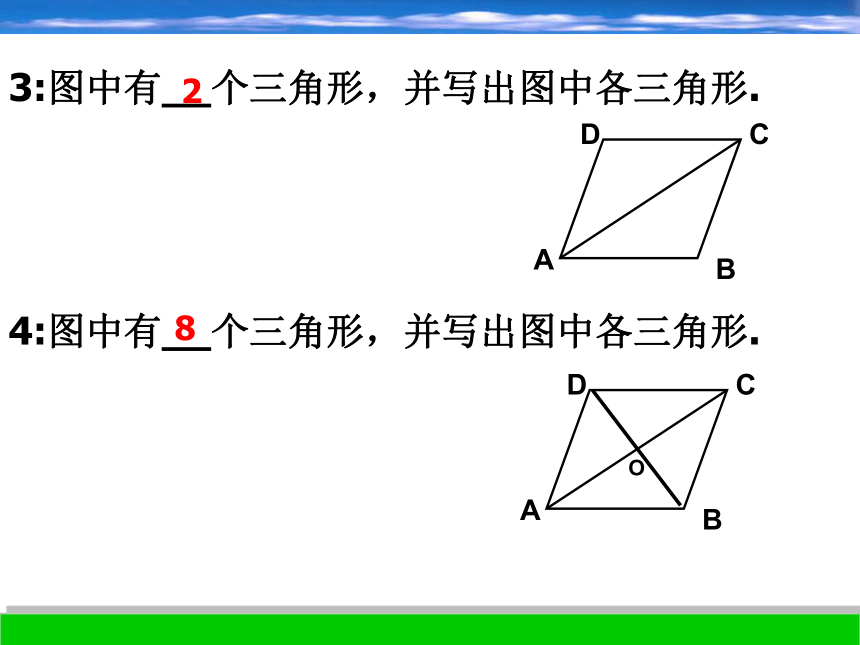
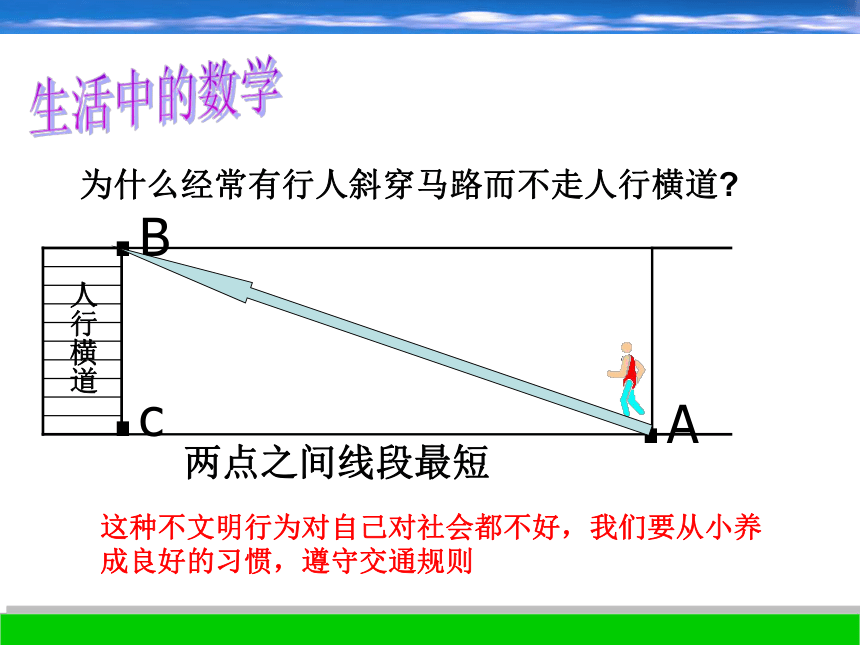
是A，B，C的三角形2:三角形表示方法(1):记做“ΔABC”(2):读做“三角形ABC”ABCBC 、 AC 、AB内角: ∠A、∠B、 ∠C点A、 点 B、 点 Cacb或a、 b、 c 三边:顶点:3:三角形的有关概念同学们都掌握了吗?咱们做个练习试试吧!ABCD1:图中有__个三角形，并写出图中各三角形.32:图中有__个三角形，并写出图中各三角形.6课堂训练1：3:图中有__个三角形，并写出图中各三角形.24:图中有__个三角形，并写出图中各三角形.8人行横道.A.B两点之间线段最短这种不文明行为对自己对社会都不好，我们要从小养
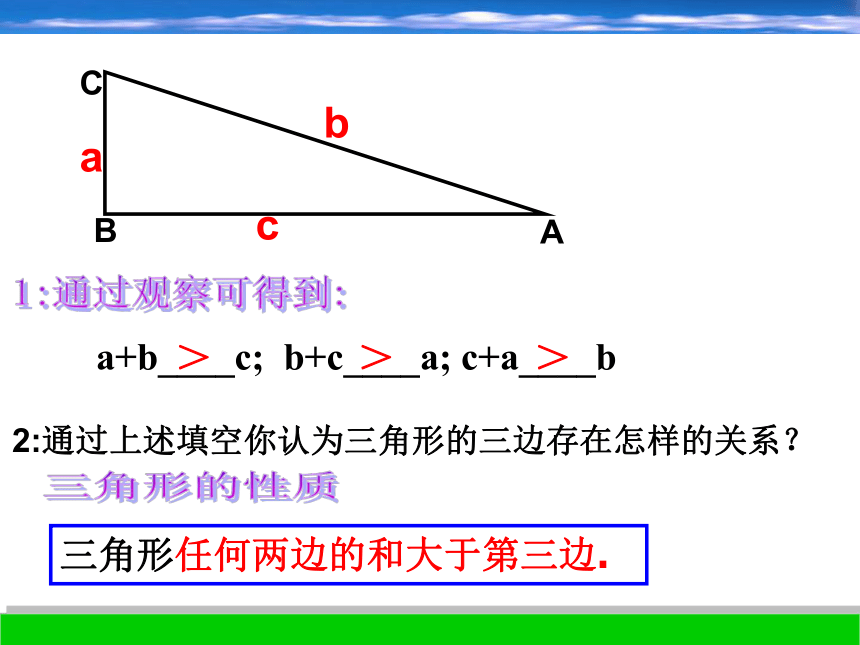
成良好的习惯，遵守交通规则.c生活中的数学 为什么经常有行人斜穿马路而不走人行横道?ABCabc1:通过观察可得到: a+b____c; b+c____a; c+a____b＞＞＞2:通过上述填空你认为三角形的三边存在怎样的关系？三角形任何两边的和大于第三边.三角形的性质三角形的三边关系:三角形的任何两边之和大于第三边a+b>cb+c>ac+a>b任何反之：在三条线段中若任两线段之和大于第三线段则这三条线段能构成一个三角形。理一理:长度为6cm, 4cm, 3cm三条线段能否组成三角形？解:∵6+4=10>3
6+3=9>4
4+3=7>6
∴能组成三角形这样判断需要三个条件，你一定希望有更好的判
断方法吧.想想看!解: ∵最长线段是6cm

4+3>6
∴能组成三角形学以致用只要满足较小的两条线段之和大于最长线 段，便可构成三角形;判断下列各组线段中，哪些能组成三角形，哪些不能组成三角形，并说明理由
1: a＝2.5cm，b＝3cm，c＝5cm；
2: e=6.3cm，f=6.3cm，g=12.6cm典型例题分析1:只要满足较小的两条线段之和大于最长线 段，便可构成三角形;判断方法：（1）找出最长线段。（2）比较大小：较短两边之和与最长线段的大小（3）判断能否组成三角形。由下列长度的三条线段能组成三角形吗?
请说明理由.(1): 1cm，2cm，3.5cm(2): 4cm，5cm，9cm(3): 6cm，8cm，13cm不能不能能课堂训练1：(4): (k+1)cm， (k+2)cm ， (2k+2)cm
其中k是正整数
a-b____c; b-c____a; a-c____b＜＜＜三角形任何两边的差小于第三边.三角形的性质三角形的任何两边之和大于第三边推广 2、一个三角形有两边相等,已知其中一边是5cm，另一边是9cm，则这个三角形的周长是______________ 1、一个三角形有两边相等,已知其中一边是3cm，另一边是9cm，则这个三角形的周长是______________21cm19cm或23cm遇到这类问题，我们通常要考虑两种情况，然后判断是否都能构成三角形课堂训练3：注意点:典型例题分析2:已知三角形的两边,如何求第三边的取值范围?两边之差?第三边?两边之和例2: 如图,如果要构成三角形,求AC的取值范围.41.若AC为整数，那么△ABC的周长= ________________________;
2.若周长为奇数，那么AC= ____________;
3.若周长为偶数，那么AC=_______;　　6或815或16或17或18或195或7或9课堂训练4：1