1.1认识三角形2

课件16张PPT。1.1 认识三角形(2)课堂测试:1:下列各组数不可能是一个三角形的边长的是（ ）C两边之差<第三边<两边之和注意:三角形三个内角的和等于1:观察与思考:根据下面的折叠,你发现在△ABC中, ∠A+∠B+∠C等于多少度?2:三角形内角和的性质:例1：1:在△ABC中，∠A＝45。， ∠B=30。， 求∠C的度数∠C= 105。定义1：有一个内角是钝角的三角形叫做钝角三角形BAC2:在△ABC中，已知∠ A=45°,
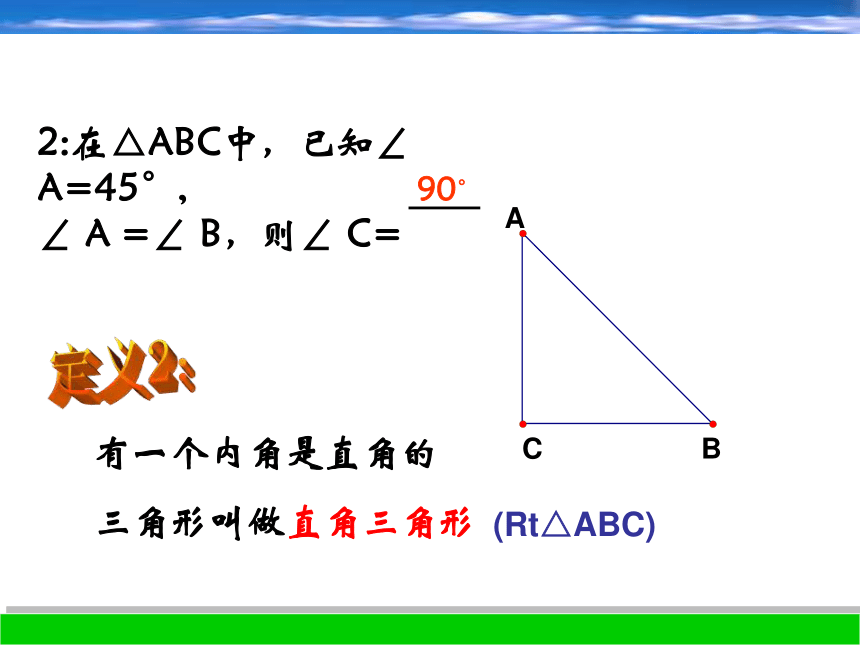
∠ A =∠ B，则∠ C= 90。有一个内角是直角的
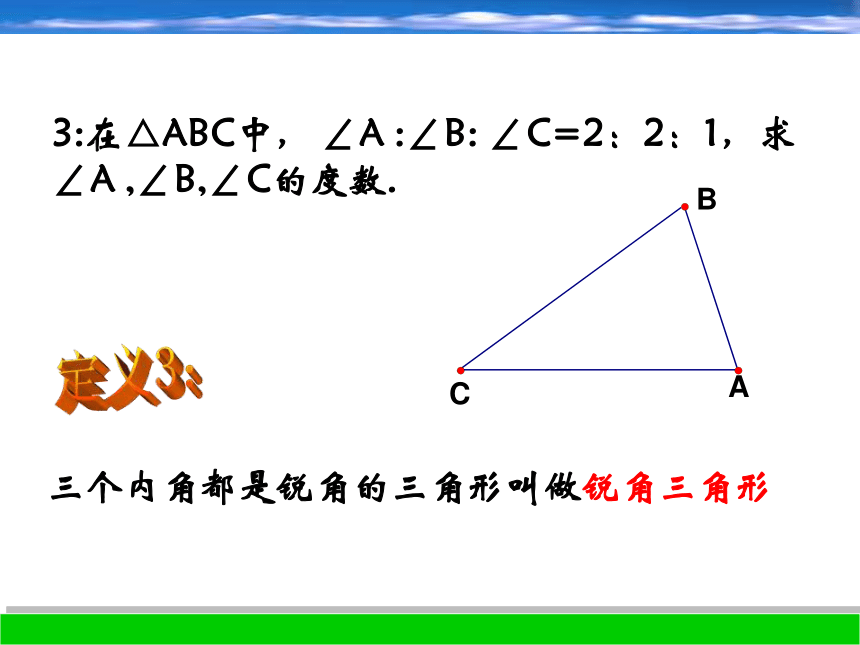
三角形叫做直角三角形定义2：(Rt△ABC)三个内角都是锐角的三角形叫做锐角三角形定义3：3:在△ABC中， ∠A :∠B: ∠C=2：2：1，求
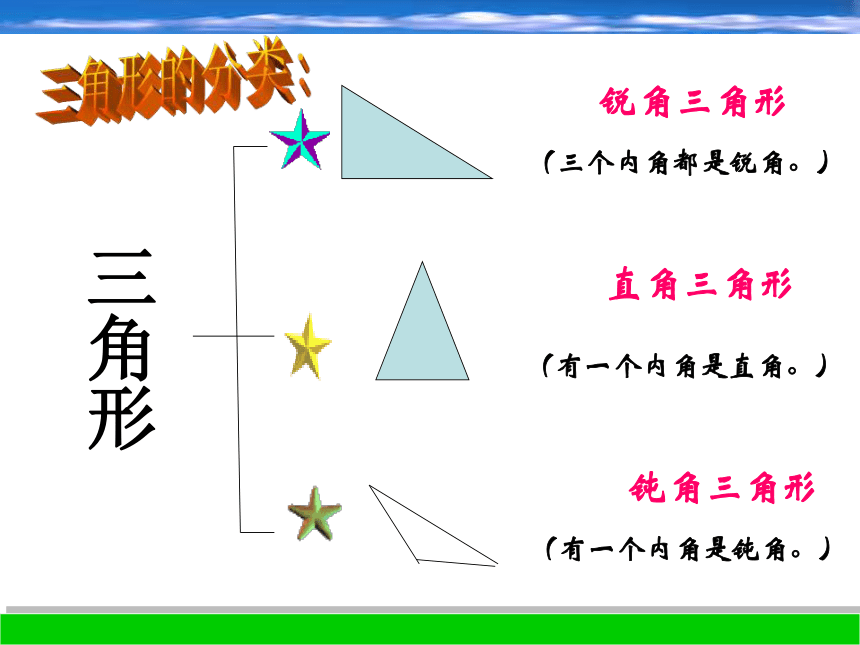
∠A ,∠B,∠C的度数.BCA锐角三角形直角三角形钝角三角形（三个内角都是锐角。）（有一个内角是直角。）（有一个内角是钝角。）三角形三角形的分类:锐角三角形直角三角形钝角三角形⑦②①③④⑤⑥①②③④⑤⑥⑦请将下列三角形分类:DBAC不相邻内角1234 ．观 察1:让我们再来认识一下与三角形的内角相关的另外一种角：三角形的外角外角与相邻内角有什么特殊关系？∠3+∠4=180°想一想：（2）∠2是______的外角，如图：∠1△ADC（1）△BCD的外角是_____1BC2DAE课堂训练1:（3） △ AEC的外角是 _____ △ADE∠AED又是______的外角观 察2 ：探索，猜想：1: ∠4=∠1+∠2 2: ∠4﹥∠1 , ∠4﹥∠2 DBAC不相邻内角1234 ． 外角与不相邻内角有什么关系？并说明理由.归纳与总结:1:三角形的一个外角等于与它不相邻的两个内角的和。三角形外角的性质：2:三角形的一个外角大于任何一个与它 不相邻的内角。
在△ABC中,已知∠A =∠B,
∠ 1=100°,求 ∠A 的度数。典型例题分析1:课堂训练2:1:如图, ∠A =25°, ∠B =40°, ∠ BFE=93°,求∠D的度数.AEBCFD2:如图,在△ABC中,∠C是直角,D是BC上的一点 .已知∠1= ∠2, ∠B =25°,求 ∠BAD 的度数。BCDA123:如图,点D在BC上，点E在AD上比较 ∠B与∠1的大小。并说明你的理由？ABCED∴ ∠1﹥∠B1∴∠EDC﹥∠B∵∠EDC是△ABD的外角解:4:如图, 已知∠ABO =20°, ∠ACO=40°, ∠BOC= 2∠A,求∠A的度数.思路:通过添加辅助线,构造运用三角形的性质的条件,并运用此性质求角的度数.