2.3 二次函数的性质
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
2.3二次函数的性质(教案)
教学目标
知识目标 从具体函数的图象中认识二次函数的基础性质,学会确定二次函数的增减性,学会确定二次函数的最大值及最小值,学会判定二次函数的值何时为零、何时为正、何时为负。
能力目标 培养学生用五点法画二次函数草图的能力,培养学生观察、分析、归纳、总结的能力。
情感目标 让学生体会数形结合的数学思想方法的教育,向学生渗透事物间互相联系,以及运动、变化的辨证唯物主义思想。
教学重点难点
重点 二次函数的最大值、最小值及增减性的理解和求法;五点法画二次函数的大致图象。
难点 二次函数性质的应用。
课堂教与学互动设计
创设情境,引入新课
同学们,你们看过《喜羊羊与灰太狼》这部动画片吗?那对红太狼拿锅砸灰太狼这一幕一定不陌生吧!假如灰太狼被砸后飞过的路线看作是一条抛物线,它究竟被抛了多高?抛了多远?你们想知道吗?那就一起走进今天的课堂。(板书课题)
合作交流,探究新知
今天,老师将与同学们一起来当一回导演,让我们来续写一集《喜羊羊与灰太狼》。故事是这样的:
新的一天开始了,灰太狼先生又开始了它的抓羊历程。这一次,它想挖一口陷阱来抓羊。所挖陷阱的横截面的外边缘是抛物线y=2x2-4x-6的一部分。请你帮它设计图纸。
画二次函数y=2x2-4x-6的图象.
1、填一填。
x … -2 -1 0 1 2 3 4 …
y … …
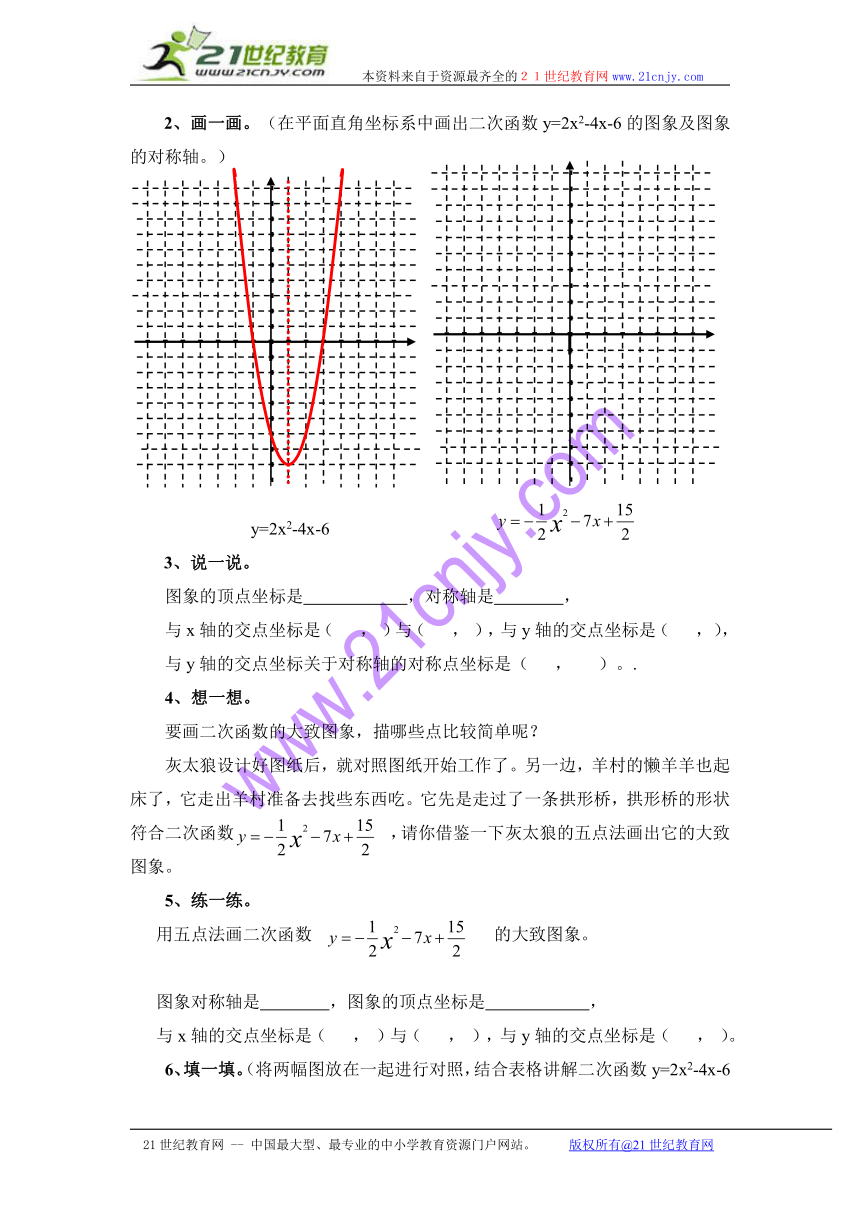
2、画一画。(在平面直角坐标系中画出二次函数y=2x2-4x-6的图象及图象的对称轴。)
y=2x2-4x-6
3、说一说。
图象的顶点坐标是 ,对称轴是 ,
与x轴的交点坐标是( , )与( , ),与y轴的交点坐标是( , ),与y轴的交点坐标关于对称轴的对称点坐标是( , )。.
4、想一想。
要画二次函数的大致图象,描哪些点比较简单呢?
灰太狼设计好图纸后,就对照图纸开始工作了。另一边,羊村的懒羊羊也起床了,它走出羊村准备去找些东西吃。它先是走过了一条拱形桥,拱形桥的形状符合二次函数 ,请你借鉴一下灰太狼的五点法画出它的大致图象。
5、练一练。
用五点法画二次函数 的大致图象。
图象对称轴是 ,图象的顶点坐标是 ,
与x轴的交点坐标是( , )与( , ),与y轴的交点坐标是( , )。
6、填一填。(将两幅图放在一起进行对照,结合表格讲解二次函数y=2x2-4x-6的增减性)
(1)对于函数y=2x2-4x-6,当x 时,y随x的增大而减小;
当x 时,y随x的增大而增大;当x 时,函数y有最小值是 。
(2)对于函数 ,当x 时,y随x的增大而增大;
当x 时,y随x的增大而减小;当x 时,函数y有最大值是 。
归纳总结
灰太狼挖好了陷阱躲在附近的草丛中等待着羊掉进去,懒羊羊睡眼朦胧的走过了拱形桥,继续前进着,一不小心掉进了陷阱。灰太狼得意极了,抓起它就往家赶,不料正撞上了锻炼回来的喜羊羊,喜羊羊不让它带走懒羊羊,经过协商,最后它们决定进行一场智力比赛,如果灰太狼胜利了它可以连同喜羊羊一起带走,如果败了,则要放了懒羊羊。
7、比一比(第一回合)
已知函数: 1、 y=-x2+3x 2、 y=3x2-2x+1 3、 y=x2-2x+1
(1)求一、二两个函数的最大值(或最小值)和对应自变量的值。
(2)它们与x轴是否有交点,若有求出图象与x轴的交点坐标。
比一比(第二回合)
已知(-1,y1), (-2,y2), (-4,y3)是抛物线 y=-2x2-8x +6上的点,则 ( )
(A) y1<y2 < y3 (B) y3 < y2 < y1
(C) y2>y1 > y3 (D) y2 > y3 > y1
思考:(1)若把抛物线改为y=-2x2-8x +m,结果会如何呢?
(2)若把抛物线改为y=-2ax2-8ax +m,结果又会如何呢?
比赛结束了,灰太狼还是输给了喜羊羊,它只能遵守诺言放了懒羊羊灰溜溜的回家了。大家想一想家里等待着它的会是什么呢?(红太狼的一击)回到课开始提出的问题。
8、用一用。
灰太狼被拍出后飞行的高度y(m)与飞行时间x(s)的关系满足y= -x2+6x.,
(1)经过多长时间,灰太狼达到它的最高点 最高点的高度是多少
(2)经过多长时间,灰太狼掉到地上
课堂小结(数学日记形式)
今天的数学课,我们与古城中学来的朱老师进行了合作,合作中,我们一起续写了动画片《喜羊羊与灰太狼》。
在这个过程中,我学到了……等数学知识,我对……还存在着疑惑。
今天与老师的合作让我觉得……
老师寄语
同学们,今天我们在续写《喜羊羊与灰太狼》的过程中,学习了二次函数的性质。希望同学们在以后的学习过程能向喜羊羊一样的灵活变通,同时拿出灰太狼这种永不言弃的精神,创造出辉煌的成绩!
布置作业
★ 书本42页课内练习;、
★ ★ 书本42页课内练习;42、43页作业题;
★ ★ ★ 书本42页课内练习;42、43页作业题;
提高:
1、已知抛物线y=ax2经过点(-2,2).
(1)求这条抛物线的解析式.
(2)求出这个二次函数的最大值或最小值.
(3)在此抛物线上有两点A(x1,y1),B(x2,y2),且x1>x2>0,试比较y1与y2的大小.
2、已知函数y= x2 -2x -3
(1)写出函数图象的顶点、图象与坐标轴的交点,以及图象与 y 轴的交点关于图象对称轴的对称点。然后画出函数图象的草图;
(2)求图象与坐标轴交点构成的三角形的面积:
(3)根据第(1)题的图象草图,说 出 x 取哪些值时,
① y=0; ② y<0; ③ y>0.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
2.3二次函数的性质(教案)
教学目标
知识目标 从具体函数的图象中认识二次函数的基础性质,学会确定二次函数的增减性,学会确定二次函数的最大值及最小值,学会判定二次函数的值何时为零、何时为正、何时为负。
能力目标 培养学生用五点法画二次函数草图的能力,培养学生观察、分析、归纳、总结的能力。
情感目标 让学生体会数形结合的数学思想方法的教育,向学生渗透事物间互相联系,以及运动、变化的辨证唯物主义思想。
教学重点难点
重点 二次函数的最大值、最小值及增减性的理解和求法;五点法画二次函数的大致图象。
难点 二次函数性质的应用。
课堂教与学互动设计
创设情境,引入新课
同学们,你们看过《喜羊羊与灰太狼》这部动画片吗?那对红太狼拿锅砸灰太狼这一幕一定不陌生吧!假如灰太狼被砸后飞过的路线看作是一条抛物线,它究竟被抛了多高?抛了多远?你们想知道吗?那就一起走进今天的课堂。(板书课题)
合作交流,探究新知
今天,老师将与同学们一起来当一回导演,让我们来续写一集《喜羊羊与灰太狼》。故事是这样的:
新的一天开始了,灰太狼先生又开始了它的抓羊历程。这一次,它想挖一口陷阱来抓羊。所挖陷阱的横截面的外边缘是抛物线y=2x2-4x-6的一部分。请你帮它设计图纸。
画二次函数y=2x2-4x-6的图象.
1、填一填。
x … -2 -1 0 1 2 3 4 …
y … …
2、画一画。(在平面直角坐标系中画出二次函数y=2x2-4x-6的图象及图象的对称轴。)
y=2x2-4x-6
3、说一说。
图象的顶点坐标是 ,对称轴是 ,
与x轴的交点坐标是( , )与( , ),与y轴的交点坐标是( , ),与y轴的交点坐标关于对称轴的对称点坐标是( , )。.
4、想一想。
要画二次函数的大致图象,描哪些点比较简单呢?
灰太狼设计好图纸后,就对照图纸开始工作了。另一边,羊村的懒羊羊也起床了,它走出羊村准备去找些东西吃。它先是走过了一条拱形桥,拱形桥的形状符合二次函数 ,请你借鉴一下灰太狼的五点法画出它的大致图象。
5、练一练。
用五点法画二次函数 的大致图象。
图象对称轴是 ,图象的顶点坐标是 ,
与x轴的交点坐标是( , )与( , ),与y轴的交点坐标是( , )。
6、填一填。(将两幅图放在一起进行对照,结合表格讲解二次函数y=2x2-4x-6的增减性)
(1)对于函数y=2x2-4x-6,当x 时,y随x的增大而减小;
当x 时,y随x的增大而增大;当x 时,函数y有最小值是 。
(2)对于函数 ,当x 时,y随x的增大而增大;
当x 时,y随x的增大而减小;当x 时,函数y有最大值是 。
归纳总结
灰太狼挖好了陷阱躲在附近的草丛中等待着羊掉进去,懒羊羊睡眼朦胧的走过了拱形桥,继续前进着,一不小心掉进了陷阱。灰太狼得意极了,抓起它就往家赶,不料正撞上了锻炼回来的喜羊羊,喜羊羊不让它带走懒羊羊,经过协商,最后它们决定进行一场智力比赛,如果灰太狼胜利了它可以连同喜羊羊一起带走,如果败了,则要放了懒羊羊。
7、比一比(第一回合)
已知函数: 1、 y=-x2+3x 2、 y=3x2-2x+1 3、 y=x2-2x+1
(1)求一、二两个函数的最大值(或最小值)和对应自变量的值。
(2)它们与x轴是否有交点,若有求出图象与x轴的交点坐标。
比一比(第二回合)
已知(-1,y1), (-2,y2), (-4,y3)是抛物线 y=-2x2-8x +6上的点,则 ( )
(A) y1<y2 < y3 (B) y3 < y2 < y1
(C) y2>y1 > y3 (D) y2 > y3 > y1
思考:(1)若把抛物线改为y=-2x2-8x +m,结果会如何呢?
(2)若把抛物线改为y=-2ax2-8ax +m,结果又会如何呢?
比赛结束了,灰太狼还是输给了喜羊羊,它只能遵守诺言放了懒羊羊灰溜溜的回家了。大家想一想家里等待着它的会是什么呢?(红太狼的一击)回到课开始提出的问题。
8、用一用。
灰太狼被拍出后飞行的高度y(m)与飞行时间x(s)的关系满足y= -x2+6x.,
(1)经过多长时间,灰太狼达到它的最高点 最高点的高度是多少
(2)经过多长时间,灰太狼掉到地上
课堂小结(数学日记形式)
今天的数学课,我们与古城中学来的朱老师进行了合作,合作中,我们一起续写了动画片《喜羊羊与灰太狼》。
在这个过程中,我学到了……等数学知识,我对……还存在着疑惑。
今天与老师的合作让我觉得……
老师寄语
同学们,今天我们在续写《喜羊羊与灰太狼》的过程中,学习了二次函数的性质。希望同学们在以后的学习过程能向喜羊羊一样的灵活变通,同时拿出灰太狼这种永不言弃的精神,创造出辉煌的成绩!
布置作业
★ 书本42页课内练习;、
★ ★ 书本42页课内练习;42、43页作业题;
★ ★ ★ 书本42页课内练习;42、43页作业题;
提高:
1、已知抛物线y=ax2经过点(-2,2).
(1)求这条抛物线的解析式.
(2)求出这个二次函数的最大值或最小值.
(3)在此抛物线上有两点A(x1,y1),B(x2,y2),且x1>x2>0,试比较y1与y2的大小.
2、已知函数y= x2 -2x -3
(1)写出函数图象的顶点、图象与坐标轴的交点,以及图象与 y 轴的交点关于图象对称轴的对称点。然后画出函数图象的草图;
(2)求图象与坐标轴交点构成的三角形的面积:
(3)根据第(1)题的图象草图,说 出 x 取哪些值时,
① y=0; ② y<0; ③ y>0.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
