3.2三角形的内切圆
图片预览


文档简介
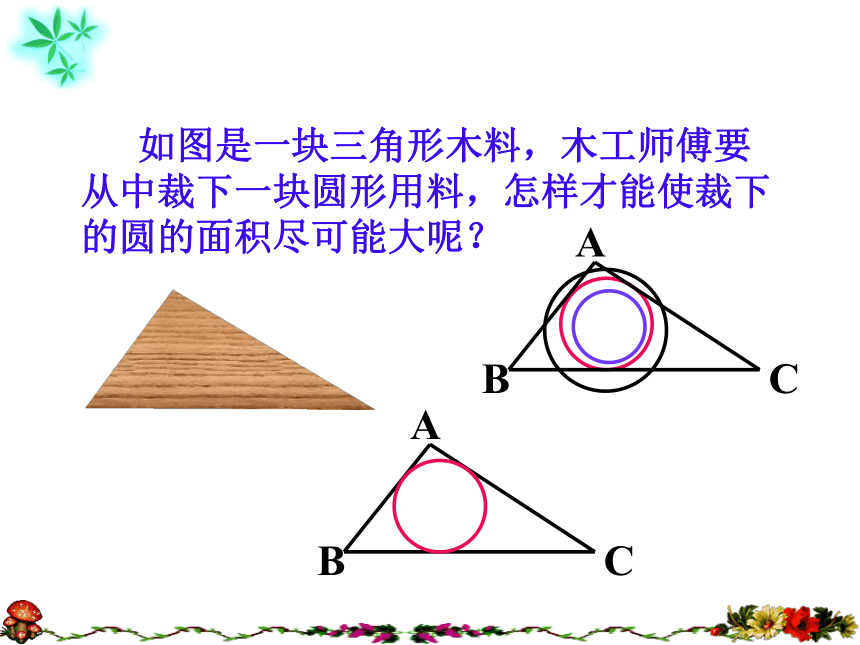
课件15张PPT。3.2 三角形的内切圆 如图是一块三角形木料,木工师傅要从中裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?已知: △ABC(如图)
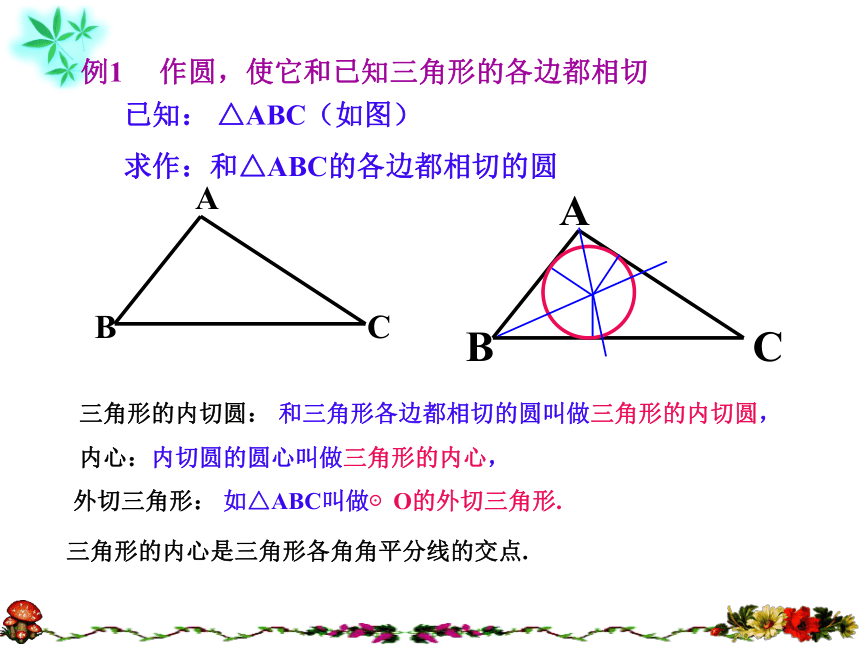
求作:和△ABC的各边都相切的圆例1 作圆,使它和已知三角形的各边都相切 三角形的内切圆: 和三角形各边都相切的圆叫做三角形的内切圆,
内心:内切圆的圆心叫做三角形的内心,
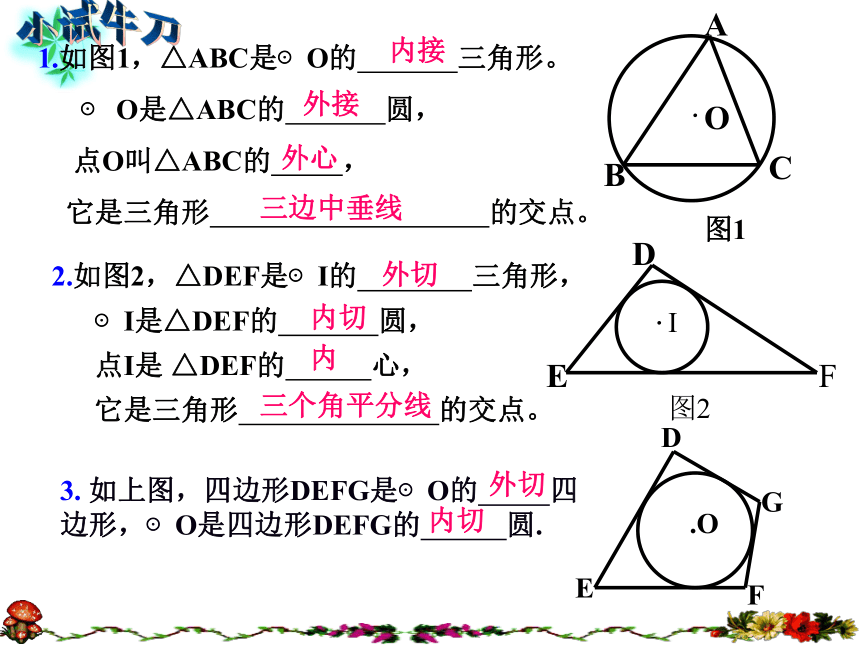
外切三角形: 如△ABC叫做⊙O的外切三角形.三角形的内心是三角形各角角平分线的交点. 1.如图1,△ABC是⊙O的 三角形。
⊙ O是△ABC的 圆,
点O叫△ABC的 ,
它是三角形 的交点。外接内接外心三边中垂线2.如图2,△DEF是⊙I的 三角形,
⊙I是△DEF的 圆,
点I是 △DEF的 心,
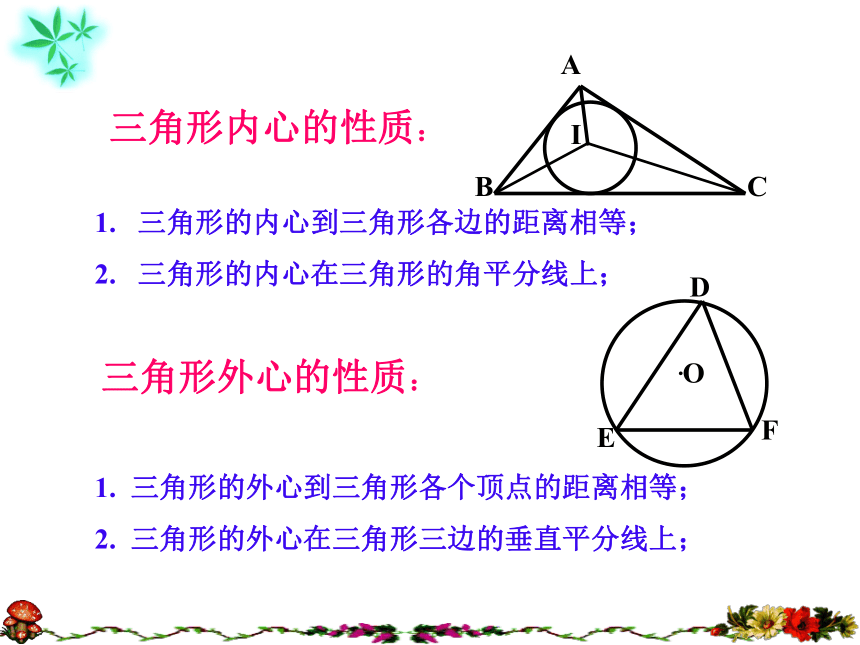
它是三角形 的交点。外切内切内三个角平分线3. 如上图,四边形DEFG是⊙O的 四边形,⊙O是四边形DEFG的 圆.内切外切小试牛刀三角形内心的性质:1. 三角形的内心到三角形各边的距离相等;
2. 三角形的内心在三角形的角平分线上; 1. 三角形的外心到三角形各个顶点的距离相等;
2. 三角形的外心在三角形三边的垂直平分线上; 三角形外心的性质:1. 三角形的内心到三角形各个顶点的距离相等( )
2. 三角形的外心到三角形各边的距离相等 ( )
3. 等边三角形的内心和外心重合; ( )
4. 三角形的内心一定在三角形的内部( )
5. 菱形一定有内切圆( )
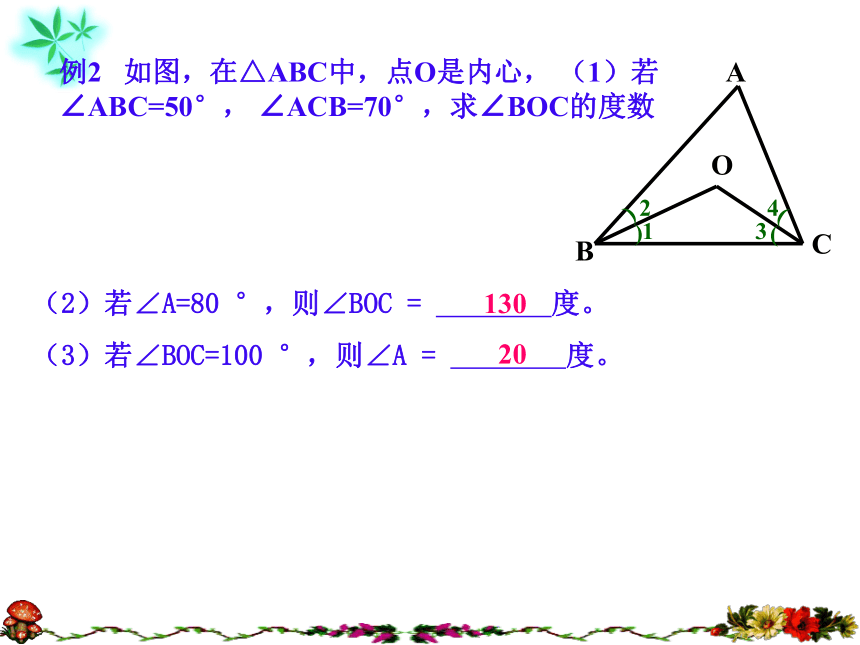
6. 矩形一定有内切圆( )错错对对 错 对判断题:(2)若∠A=80 °,则∠BOC = 度。
(3)若∠BOC=100 °,则∠A = 度。13020理由: ∵点O是△ABC的内心,∴ ∠1+ ∠3 = (∠ABC+ ∠ACB)∴ ∠1= ∠ABC, ∠3= ∠ACB= 180 °-( 90 ° - ∠A )= (180 ° - ∠A )= 90 °+ ∠A= 90 ° - ∠A答: ∠BOC =90 ° + ∠A(4)试探索: ∠A与∠BOC之间存在怎样的数量关系?请说明理由。在△OBC中,∠BOC =180 °-( ∠1+ ∠3 ) 如图,O是△ABC的内心, ∠BAC与∠BOC有何数量关系? 试着作一推导.探讨1:
结论:D例3、如图,一个木模的上部是圆柱,下部是底面为等边三角形的直棱柱.圆柱的下底面圆是直三棱柱上底面等边三角形的内切圆.已知直三棱柱的底面等边三角形边长为3cm,求圆柱底面的半径。探讨2:
设△ABC 的内切圆的半径为r,△ABC 的各边长之和为L,△ABC 的面积S,我们会有什么结论?DEF三角形面积
(L为三角形周长,r为内切圆半径)r?OBA? 探讨3:
设△ABC是直角三角形,∠C=90°,它
的内切圆的半径为r,△ABC 的各边长分别为a、b、c,试探讨r与a、b、c的关系.
C┛cbaFEDr结论:例 3:已知:如图,⊙O是△ABC的内切圆,切点分别为D,E,F.
设△ABC的周长为 。求证:AE+BC=ABCFDE.O已知:在△ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F,求AF、BD和CE的长。ABCFDExx13-x13-x9-x9-x结论:AF=4
BD=9
CE=5 1. 三角形内切圆的作法 .
2. 三角形的外接圆与圆的内接三角形
三角形的内切圆与圆的外切三角形
多边形的内切圆与圆的外切多边形
3. 学习时要明确“接”和“切”的含义、弄清“内心”与
“外心”的区别,
4. 利用三角形内心的性质解题时,要注意整体思想的运
用。课堂小结:
求作:和△ABC的各边都相切的圆例1 作圆,使它和已知三角形的各边都相切 三角形的内切圆: 和三角形各边都相切的圆叫做三角形的内切圆,
内心:内切圆的圆心叫做三角形的内心,
外切三角形: 如△ABC叫做⊙O的外切三角形.三角形的内心是三角形各角角平分线的交点. 1.如图1,△ABC是⊙O的 三角形。
⊙ O是△ABC的 圆,
点O叫△ABC的 ,
它是三角形 的交点。外接内接外心三边中垂线2.如图2,△DEF是⊙I的 三角形,
⊙I是△DEF的 圆,
点I是 △DEF的 心,
它是三角形 的交点。外切内切内三个角平分线3. 如上图,四边形DEFG是⊙O的 四边形,⊙O是四边形DEFG的 圆.内切外切小试牛刀三角形内心的性质:1. 三角形的内心到三角形各边的距离相等;
2. 三角形的内心在三角形的角平分线上; 1. 三角形的外心到三角形各个顶点的距离相等;
2. 三角形的外心在三角形三边的垂直平分线上; 三角形外心的性质:1. 三角形的内心到三角形各个顶点的距离相等( )
2. 三角形的外心到三角形各边的距离相等 ( )
3. 等边三角形的内心和外心重合; ( )
4. 三角形的内心一定在三角形的内部( )
5. 菱形一定有内切圆( )
6. 矩形一定有内切圆( )错错对对 错 对判断题:(2)若∠A=80 °,则∠BOC = 度。
(3)若∠BOC=100 °,则∠A = 度。13020理由: ∵点O是△ABC的内心,∴ ∠1+ ∠3 = (∠ABC+ ∠ACB)∴ ∠1= ∠ABC, ∠3= ∠ACB= 180 °-( 90 ° - ∠A )= (180 ° - ∠A )= 90 °+ ∠A= 90 ° - ∠A答: ∠BOC =90 ° + ∠A(4)试探索: ∠A与∠BOC之间存在怎样的数量关系?请说明理由。在△OBC中,∠BOC =180 °-( ∠1+ ∠3 ) 如图,O是△ABC的内心, ∠BAC与∠BOC有何数量关系? 试着作一推导.探讨1:
结论:D例3、如图,一个木模的上部是圆柱,下部是底面为等边三角形的直棱柱.圆柱的下底面圆是直三棱柱上底面等边三角形的内切圆.已知直三棱柱的底面等边三角形边长为3cm,求圆柱底面的半径。探讨2:
设△ABC 的内切圆的半径为r,△ABC 的各边长之和为L,△ABC 的面积S,我们会有什么结论?DEF三角形面积
(L为三角形周长,r为内切圆半径)r?OBA? 探讨3:
设△ABC是直角三角形,∠C=90°,它
的内切圆的半径为r,△ABC 的各边长分别为a、b、c,试探讨r与a、b、c的关系.
C┛cbaFEDr结论:例 3:已知:如图,⊙O是△ABC的内切圆,切点分别为D,E,F.
设△ABC的周长为 。求证:AE+BC=ABCFDE.O已知:在△ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F,求AF、BD和CE的长。ABCFDExx13-x13-x9-x9-x结论:AF=4
BD=9
CE=5 1. 三角形内切圆的作法 .
2. 三角形的外接圆与圆的内接三角形
三角形的内切圆与圆的外切三角形
多边形的内切圆与圆的外切多边形
3. 学习时要明确“接”和“切”的含义、弄清“内心”与
“外心”的区别,
4. 利用三角形内心的性质解题时,要注意整体思想的运
用。课堂小结:
