5.2平行四边形

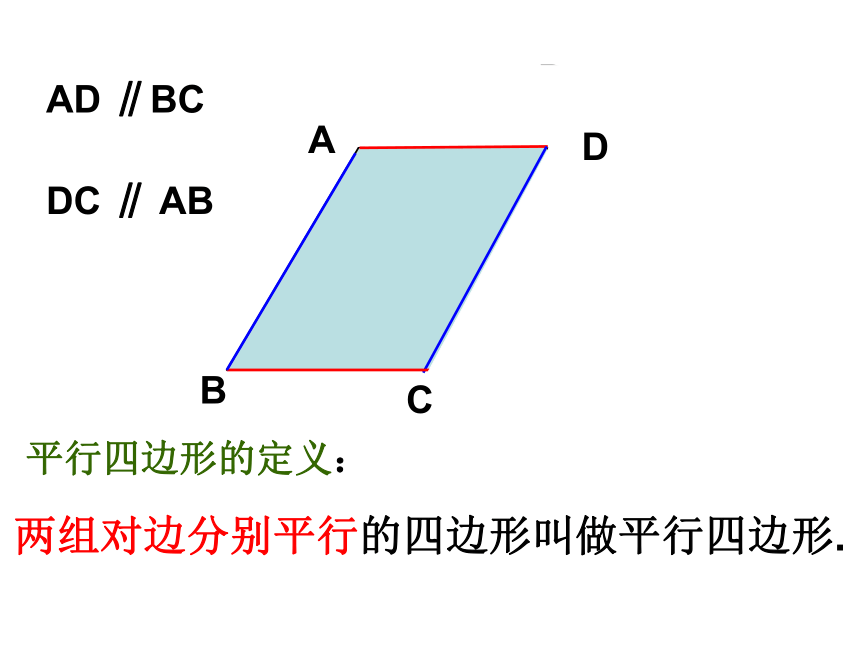
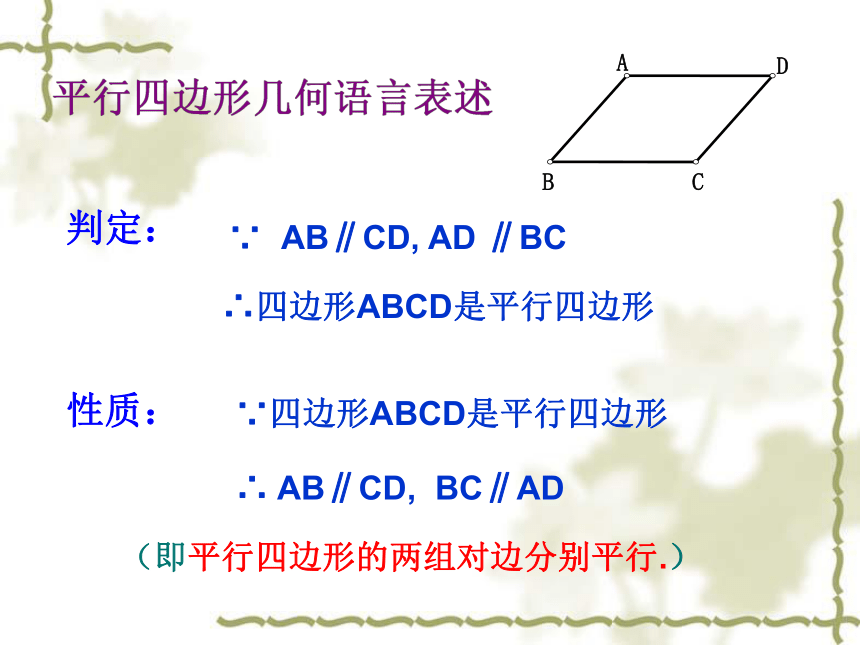
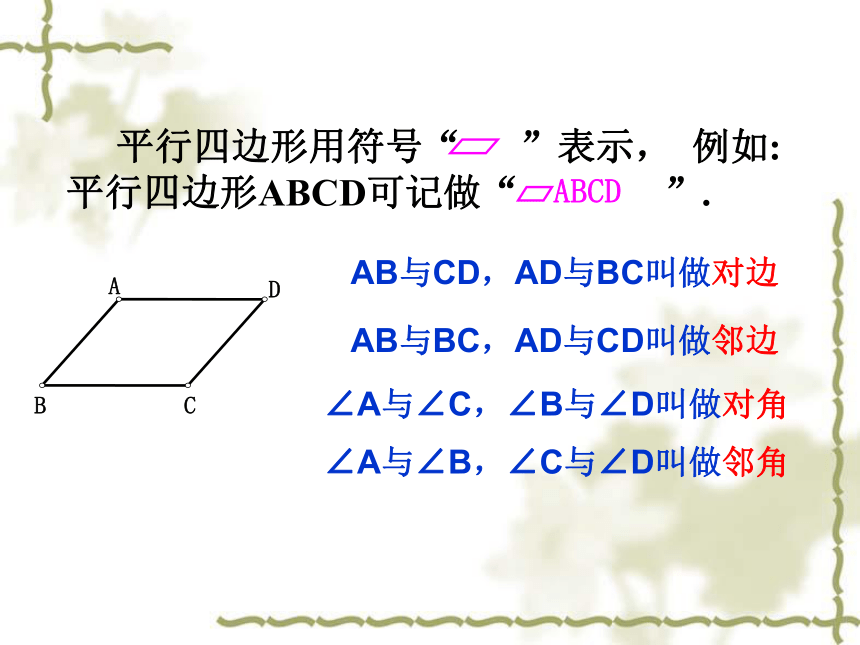
课件20张PPT。5.2 平行四边形 两组对边分别平行的四边形叫做平行四边形.平行四边形的定义：AD ∥BCDC ∥ AB∴四边形ABCD是平行四边形∴ AB∥CD, BC∥AD判定：∵ AB∥CD, AD ∥BC性质：∵四边形ABCD是平行四边形（即平行四边形的两组对边分别平行.）∠A与∠C，∠B与∠D叫做对角AB与CD，AD与BC叫做对边∠A与∠B，∠C与∠D叫做邻角AB与BC，AD与CD叫做邻边 有两块形状和大小完全相同的直角三角板，你能拼出平行四边形吗？试试看.
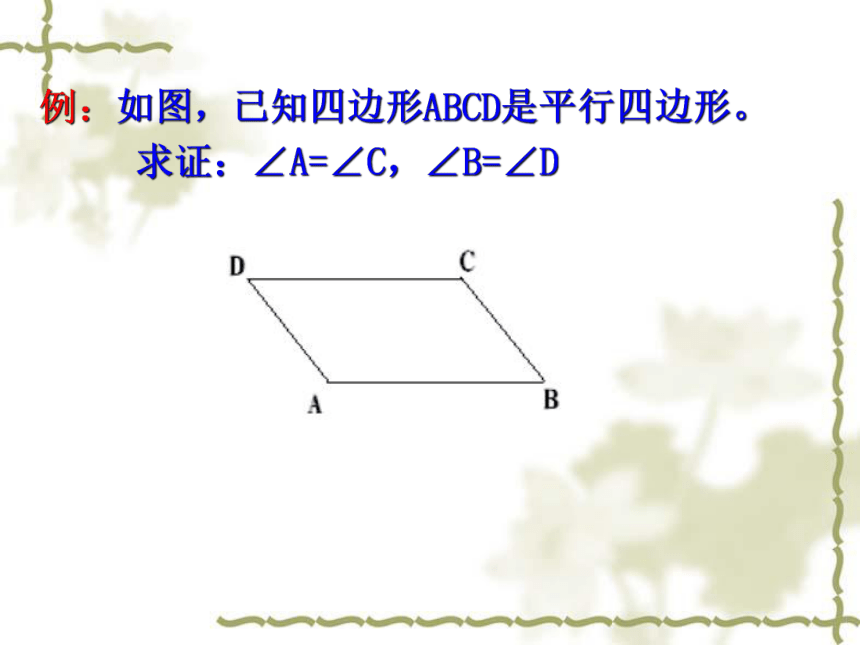
拼一拼例：如图，已知四边形ABCD是平行四边形。
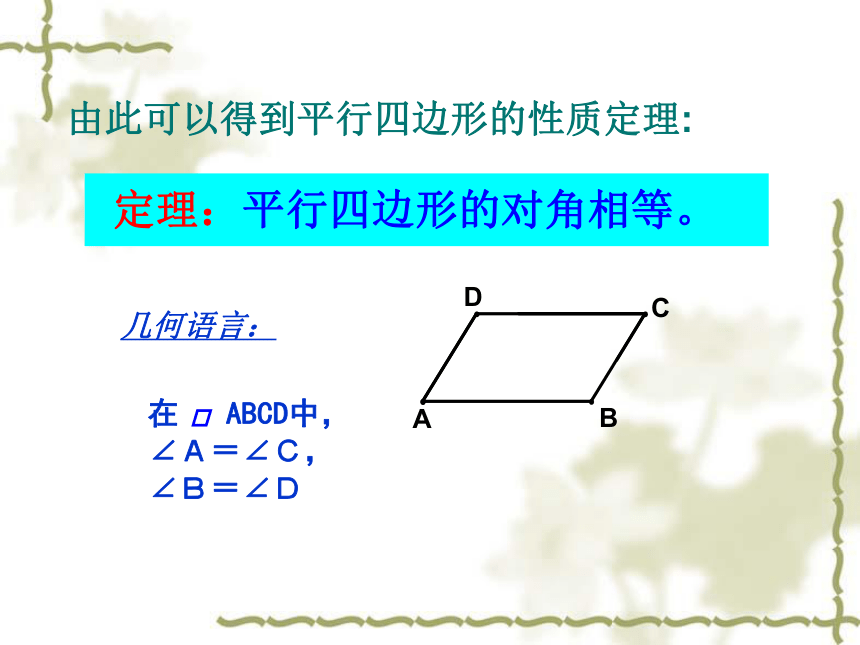
求证：∠A=∠C，∠B=∠D几何语言： 定理：平行四边形的对角相等。由此可以得到平行四边形的性质定理:2、已知平行四边形相邻两个角的度数之比为3:2,则平行四边形的各个内角的度数分别为
___________________ .125o55o125o108o、72o、108o、72o3、已知平行四边形的最大角比最小角大100o ,那么平行四边形的各个内角的度数分别为
___________________ .40o、140o、40o、140o你能举例生活中平行四边形的应用吗？请你来帮忙！ 学校买了四棵树，准备栽在花园里，已经栽了三棵（如图），现在学校希望这四棵树能组成一个平行四边形，你觉得第四棵树应该栽在哪里？课内练习方案设计：若你手中只有卷尺这一样工具，你能设计一个满足上述条件的方案吗，使得道路AECF的两条边AF、CE分别平分□ ABCD的两个对角？1、平行四边形的定义：两组对边分别平行 的四边形. 2、平行四边形的对角相等.3、平行四边形的不稳定性在实际生活中的应用.小结知识点：重要的数学思想方法：转化小结特殊到一般布置作业1、课后作业题
2、作业本（2）谢谢