5.1多边形（3）

课件37张PPT。义务教育课程标准实验教科书　
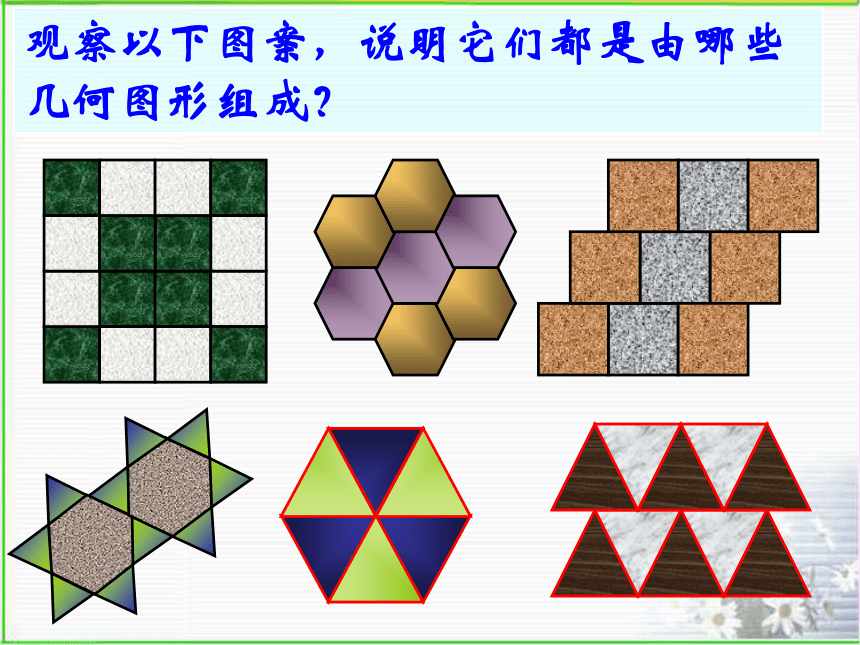
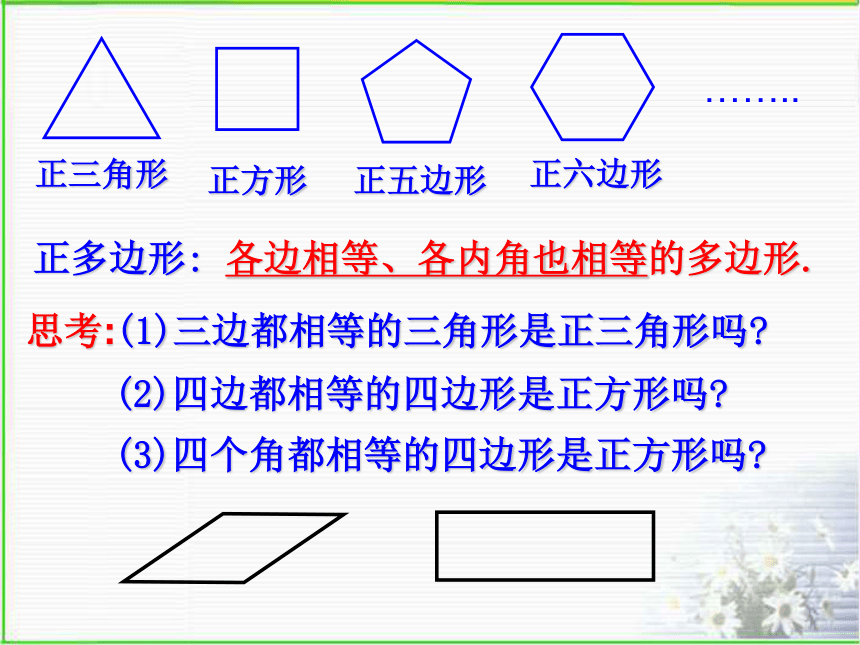
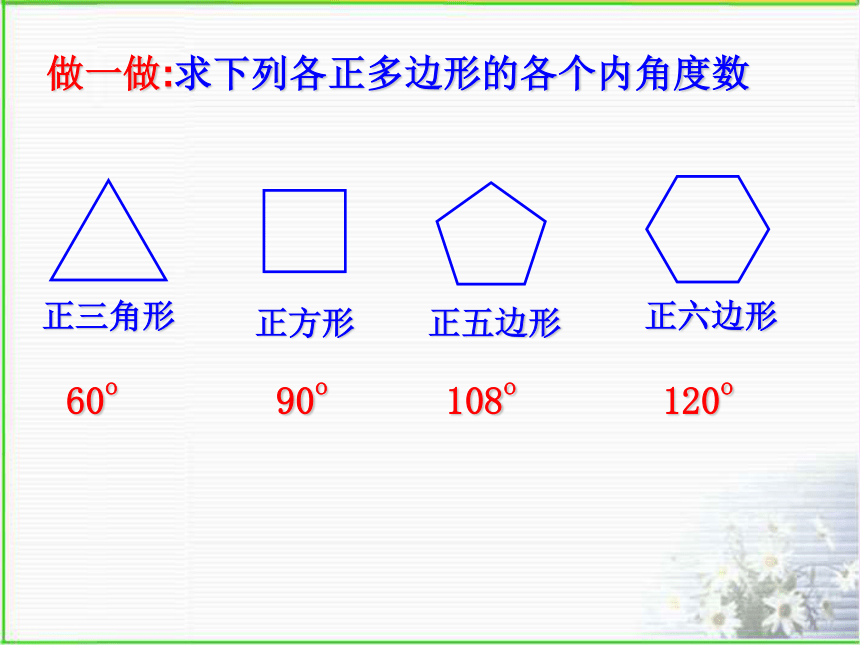
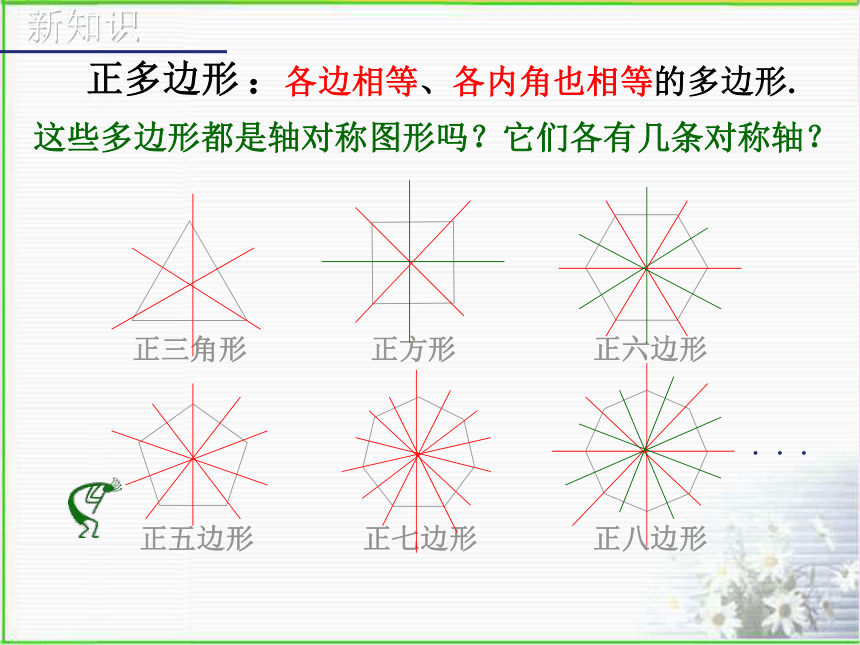
浙江版《数学》八年级下册5.1 多边形(3)请你欣赏观察以下图案，说明它们都是由哪些几何图形组成？正多边形:各边相等、各内角也相等的多边形.思考:(1)三边都相等的三角形是正三角形吗?(2)四边都相等的四边形是正方形吗?(3)四个角都相等的四边形是正方形吗?做一做:求下列各正多边形的各个内角度数60o90o108o120o新知识正三角形正方形正六边形正五边形正七边形正八边形正多边形：各边相等、各内角也相等的多边形.这些多边形都是轴对称图形吗？它们各有几条对称轴？．．．练一练:(1)正十边形的每个内角为_____度144(2)一个正多边形的内角和为1260o,那么这个正多边形有______条边,它的一个外角是_____度.940想一想:
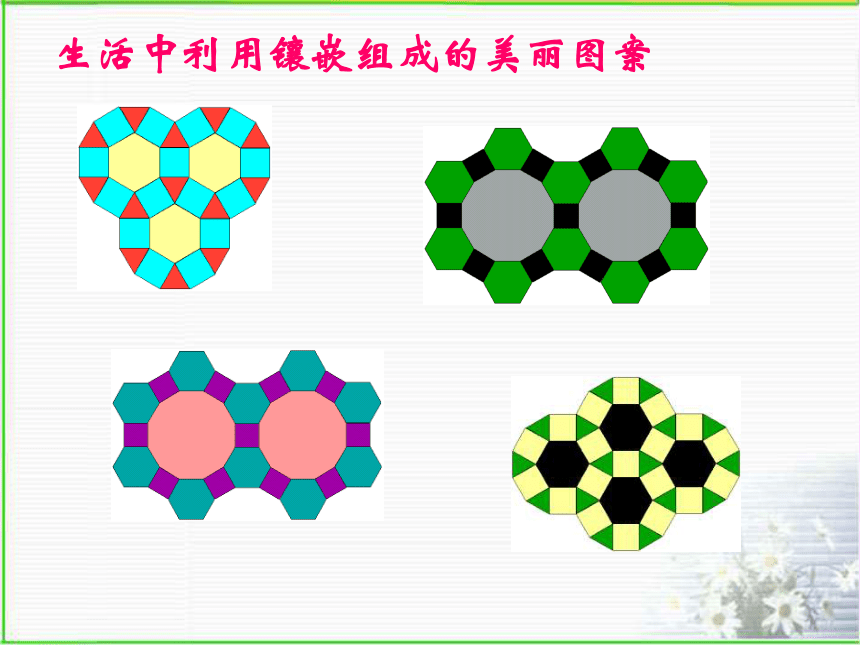
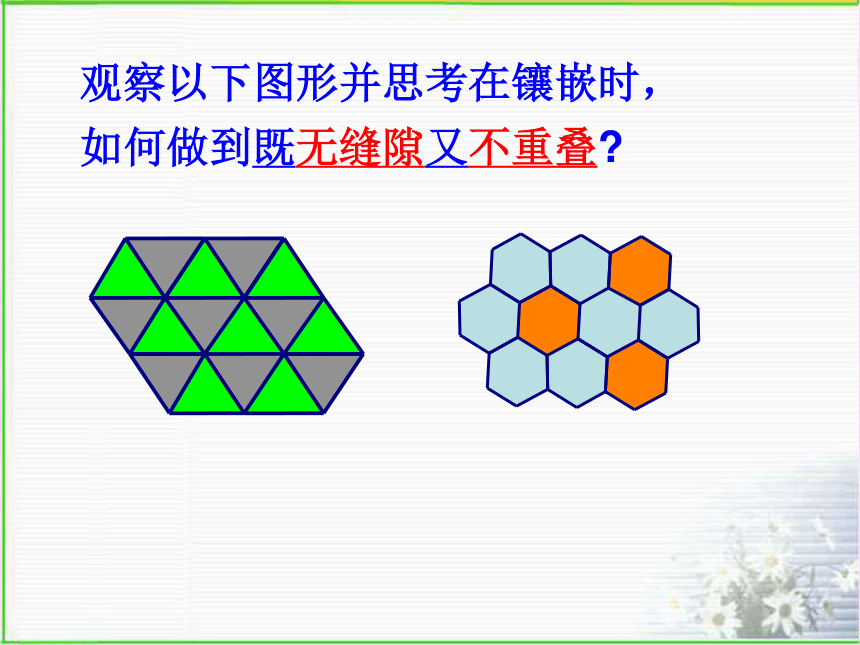
利用刻度尺和量角器你能画正三角形，正方形，正五边形，正六形，正八边形吗？用一种或几种多边形进行拼接,彼此之间不留缝隙,也不重叠地铺成一片,叫做平面图形的镶嵌.生活中利用镶嵌组成的美丽图案 你注意到地砖的形状一般都是几边形吗？有没有正五边形地砖？你知道为什么吗？ 分别用若干个正三角形、正方形、正五边形、正六边形的纸片,在一张桌面上尝试镶嵌.你发现这几种正多边形中,哪些能单独镶嵌平面，哪些不能?你能说明其中的原因吗? 合作学习:观察以下图形并思考在镶嵌时，如何做到既无缝隙又不重叠?正三角形为什么能镶嵌？正方形为什么能镶嵌？123∠1+∠2+∠3=?正五边形可以镶嵌吗？原来拼不了！为什么?正五边形不能密铺!正六边形为什么能镶嵌？正多边形能否镶嵌平面,关键是拼接点处的几个内角和能否构成360°.还有其他的正多边形可以进行镶嵌吗？正多边形能镶嵌平面的数学原理：　用正多边形来镶嵌平面，共顶点的各角之和必须是３６０度；能能能正三角形正方形正五边形正六边形643不能能单独镶嵌平面的正多边形只有3种，即正三角形、正方形、正六边形.综合上述研究，可得出以下结论：1.三角形可以作平面镶嵌吗? 若能，三角形将如何镶嵌呢?探究：普通多边形的镶嵌 形状、大小完全相同的任意 三角形可以镶嵌平面吗？如图,四边形ABCD中,因为∠A+∠B+∠C+ ∠D = 360°,所以四边形也可以作平面镶嵌.2.四边形呢?探究：普通多边形的镶嵌 形状、大小完全相同的任意四边形 可以镶嵌平面吗？ 从而发现： 形状、大小完全相同的平面图形 能够镶嵌平面的有： 任意三角形、任意四边形、正六边形.探究多种正多边形的组合镶嵌平面解：因为正八边形的内角为135o， 正方形的内角为90o，根据： 135o×2+90o＝360o，可知： 两个正八边形和一个正方形 能拼成一幅镶嵌图.例:用边长相同的正四边形和正八边形做平面密铺，有几种可能？为什么？在公共的顶点处各正多边形的内角和等于360°探究活动 请选择两种能镶嵌平面的正多边形，动手试一试，组成一幅镶嵌图，然后完成以下工作：
⑴ 说明你选择的两种正多边形能镶嵌平面的数学原理；
⑵ 画出你选择的两种正多边形镶嵌平面的图形（示意图）.小结与反思1.镶嵌的要求：无缝隙，不重叠2.多边形能否镶嵌的条件：每个顶点处几个角的和为360°请你欣赏：正方形和正三角形的组合镶嵌正六边形和正三角形的组合镶嵌正六边形和正三角形的组合镶嵌正方形、正八边形的组合镶嵌正三角形、正方形、正六边形的组合镶嵌正三角形、正十二边形的组合镶嵌作业布置
（１）见作业本
（２）试试看:请你用两种或两种以上的多边形设计镶嵌图案.练习一1. 形状、大小完全相同的任意三角形、四边形 能否单独作镶嵌 ( )
2. 用任意三角形镶嵌平面时,同一顶点处应摆放 ( )个三角形;用任意四边形镶嵌平面时， 同一顶点处应摆放( )个四边形.
3.下面四种正多边形中,用同一种图形不能平面 镶嵌的是( ). 能64C