5.4中心对称

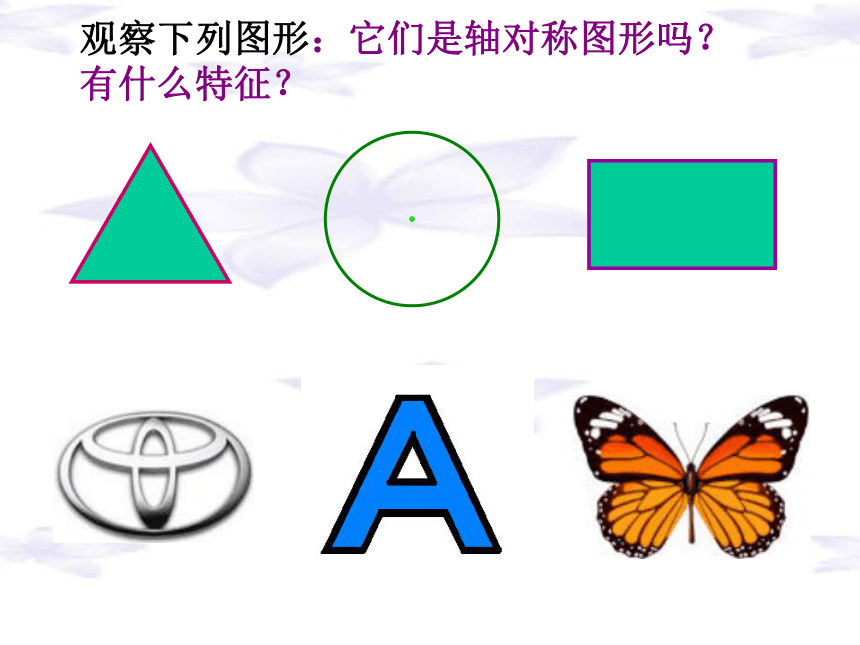
课件27张PPT。5.4 中心对称回顾与思考我们已学过哪些图形变换？轴对称变换、平移变换、旋转变换、相似变换。这幅图案有哪些变换？90°、180°、270°。观察下列图形：它们是轴对称图形吗？有什么特征？合作学习、探索新知。
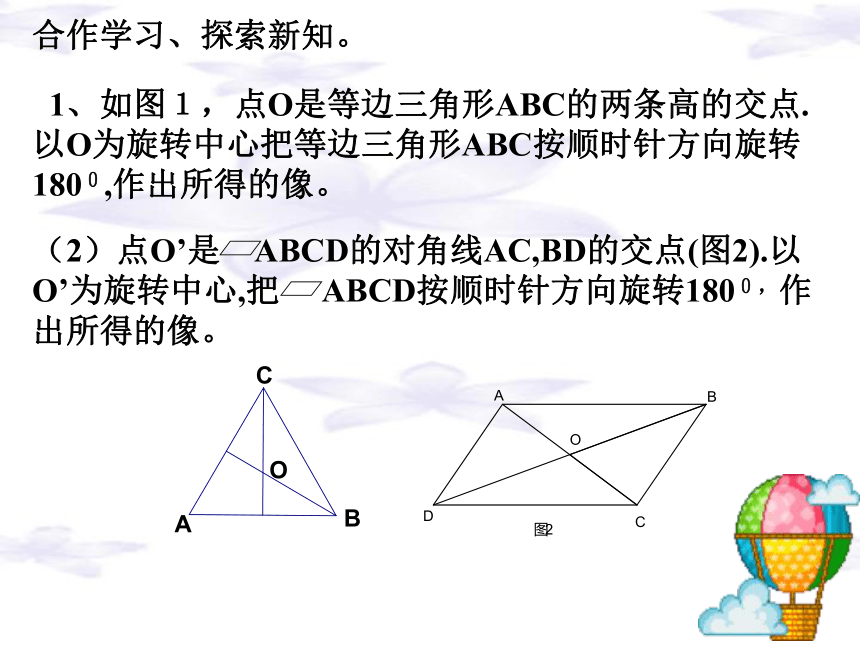
1、如图１，点O是等边三角形ABC的两条高的交点. 以O为旋转中心把等边三角形ABC按顺时针方向旋转180０,作出所得的像。
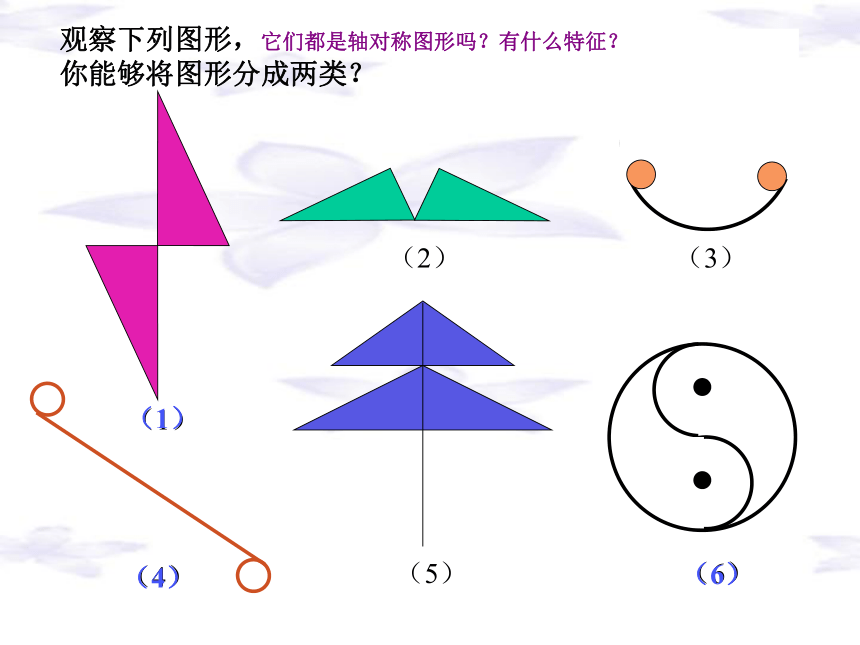
（2）点O’是　ABCD的对角线AC,BD的交点(图2).以O’为旋转中心,把 　ABCD按顺时针方向旋转180０，作出所得的像。观察下列图形，它们都是轴对称图形吗？有什么特征？
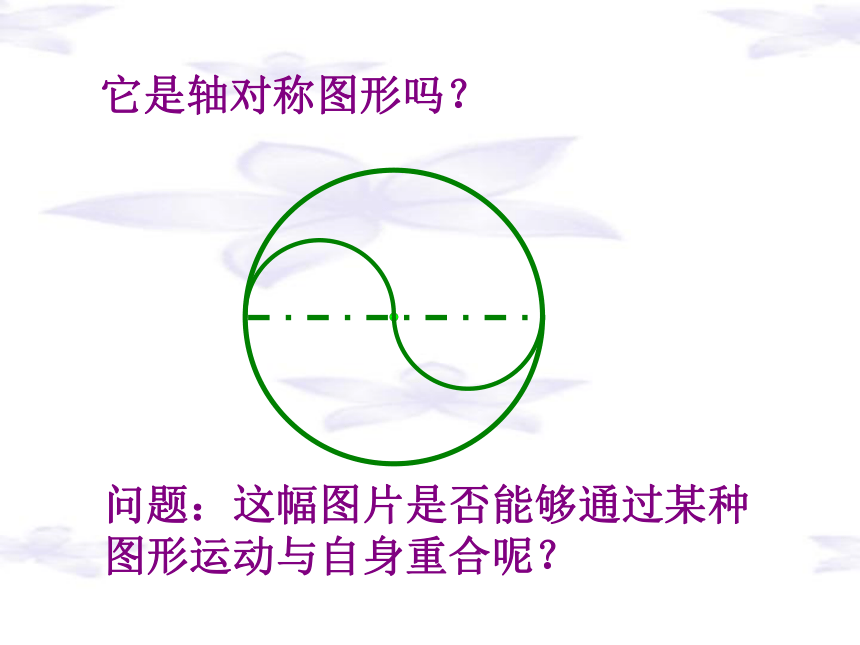
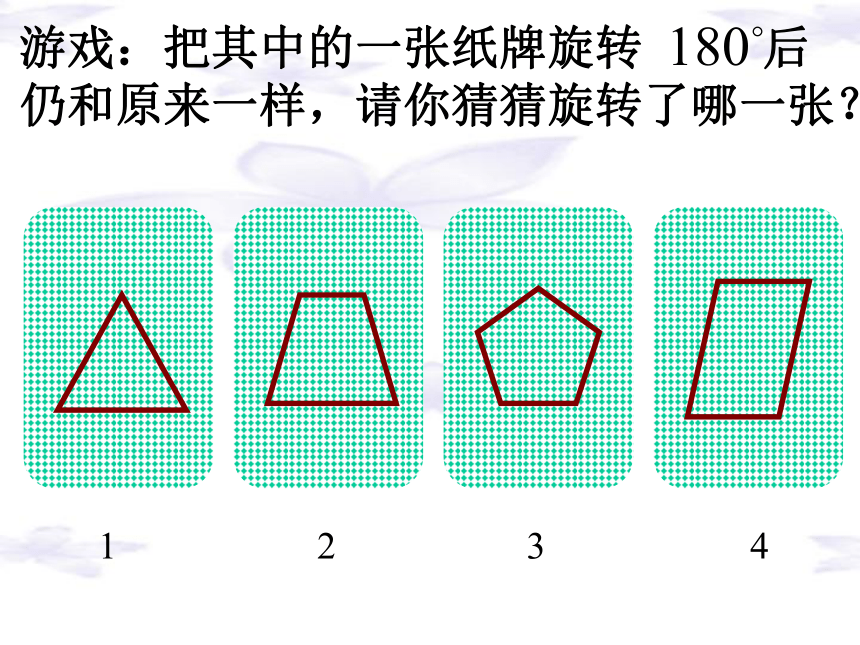
你能够将图形分成两类？（1）（6）（5）（3）（2）（4）（4）（6）（1）它是轴对称图形吗？问题：这幅图片是否能够通过某种图形运动与自身重合呢？ 如果一个图形绕着一个点旋转180o后，所得到的图形能够和原来的图形互相重合，那么这个图形叫做中心对称图形，这个点叫做它的对称中心。你能给“中心对称图形”下一个定义吗？1234游戏：把其中的一张纸牌旋转 后
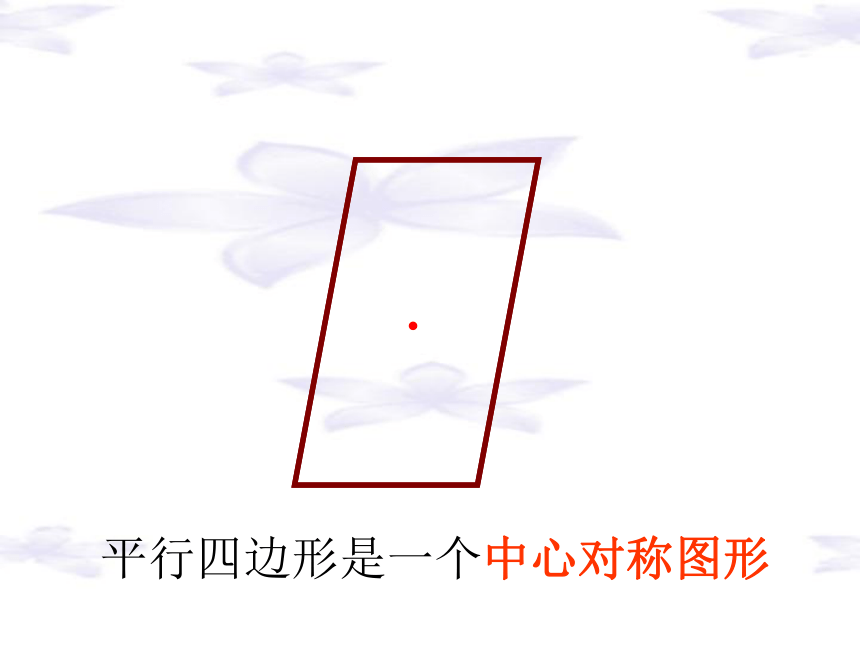
仍和原来一样，请你猜猜旋转了哪一张？平行四边形是一个中心对称图形练习
如图，在平行四边形ABCD中，AC与BD交于点O，过点O的两条直线，分别交各边与点E、H、F、G，则A、E、D、G关于O的对称点分别是 ——、——、——、—— DGFABHECOHFBC做一做：下列哪些图形是中心对称图形？（１）（２）（３）（４） 如果一个图形绕着一个点O旋转1800后,能够和另外一个图形互相重合,我们就称这两个图形关于点O成中心对称 ，这个点O叫做对称中心，能够互相重合的一对点叫做对称点。中心对称的两个图形是全等形。O中心对称中心对称图形的性质：
对称中心平分连结两个对称点的线段如下图，若A、B关于点O成中心对称，
∴点O是A、B的对称中心。
∴OA=OBEF经过点O，分别交AB、CD于E、F。解： ∵平行四边形是中心对称图形，O是对称中心∴点E、F是关于点O的对称点。
∴OE=OF。中心对称的作图AOA'连结OA，并延长到A’，使OA’=OA，例1、已知A点和O点，画出点A关于点O的对称点A'则A’是所求的点例2、已知线段AB和O点，画出线段AB关于点O的
对称线段A’B’OA'B'AB连结AO并延长到A’，使OA’＝OA，
则得A的对称点A’连结BO并延长到B’，使OB’＝OB，
则得B的对称点B’连结A’B’，则线段A’B’是所画线段例3、已知△ABC和点O，作△ A′B′C′，使△A′B′C′与△ABC关于点O成中心对称。．OＡＣＢ轴对称图形中心对称图形123翻转前后的图形完全重合旋转前后的图形完全重合中心对称图形与轴对称图形有什么区别与联系？议一议4对应点的连线被对称轴垂直平分对称中心平分连结两个对称点的线段规律：过两个中心对称图形的中心画出一条直线即可画一画动手画一画 你能画一条直线，将以下正方形分成形状大小完全相同的两部分吗?动手找一找转一转，想一想·A·Ａ′·O动手摆一摆一、填空1.如图, ABCD的对角线AC、BD交于O
C点B点线段CB平行四边形CDAB练习1) A点关于O点的对称点是 ；2) D点关于O点的对称点是 ；3)线段AD关于O点的对称线段是
；4) ABCD关于O点的对称图形是 。O