3.5弧长与扇形的面积(1)

课件22张PPT。铅球场地纸扇计时器台秤3.5 与浙教版九年级上册第3章圆的基本性质扇形的面积弧长一、教学目标：知识与技能目标：
①使学生认清弧与扇形概念上的本质差异性，以及相互之间的关联；
②掌握弧长与扇形面积的计算公式，并会简单应用公式解决问题；过程性（程序性）目标：
①让学生在经历探索弧长与扇形面积公式的过程中，引导学生运用归纳、类比的方法，使学生感受知识的生成过程；
②把多媒体有机的融入课堂，巧妙借用多媒体的直观性，激发师生、生生互动，培养学生的具象思维能力，从而培养空间感；情感与价值观目标：
①使学生在经历数学观察、归纳探索、类比、生成的过程中培养学生科学的学习态度；
②使学生领会运用数（如：弧长与扇形公式的生成规律）的方法去研究、揭示图形变化规律。二、教学重点与难点：
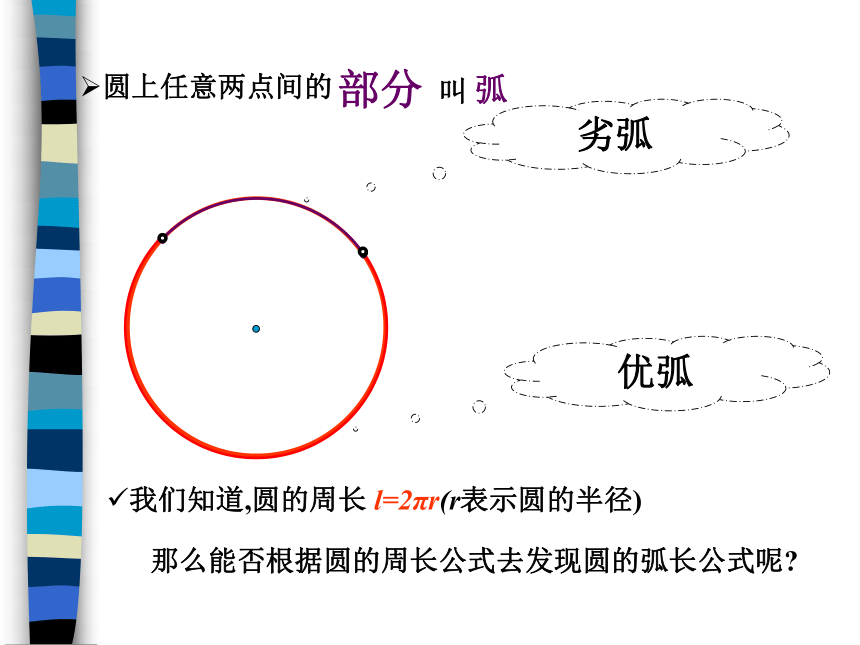
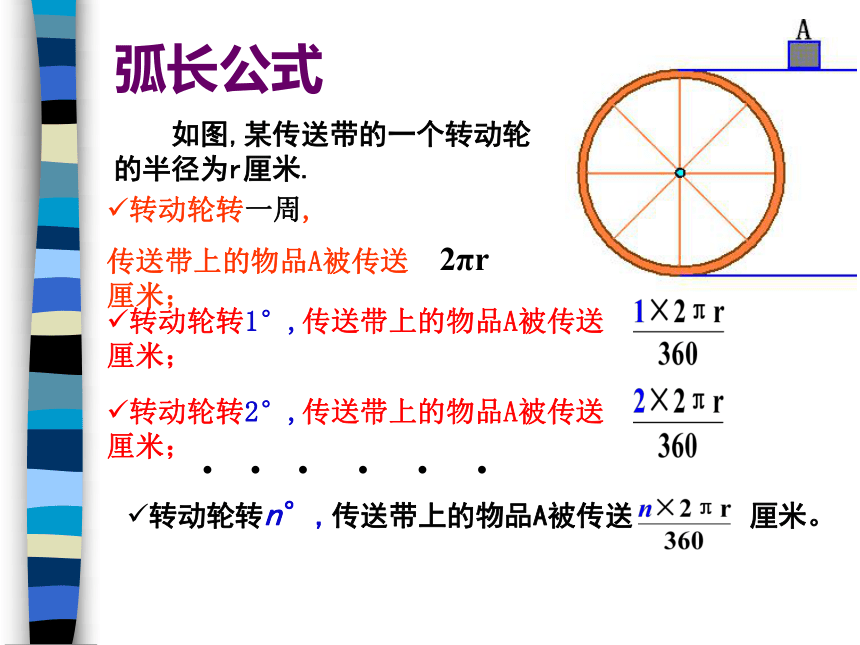
弧长与扇形面积的计算公式，及应用圆上任意两点间的部分叫 弧劣弧优弧我们知道,圆的周长 l=2πr(r表示圆的半径)那么能否根据圆的周长公式去发现圆的弧长公式呢? 如图,某传送带的一个转动轮的半径为r厘米.转动轮转1°,传送带上的物品A被传送 厘米；转动轮转n°,传送带上的物品A被传送 厘米。转动轮转一周,
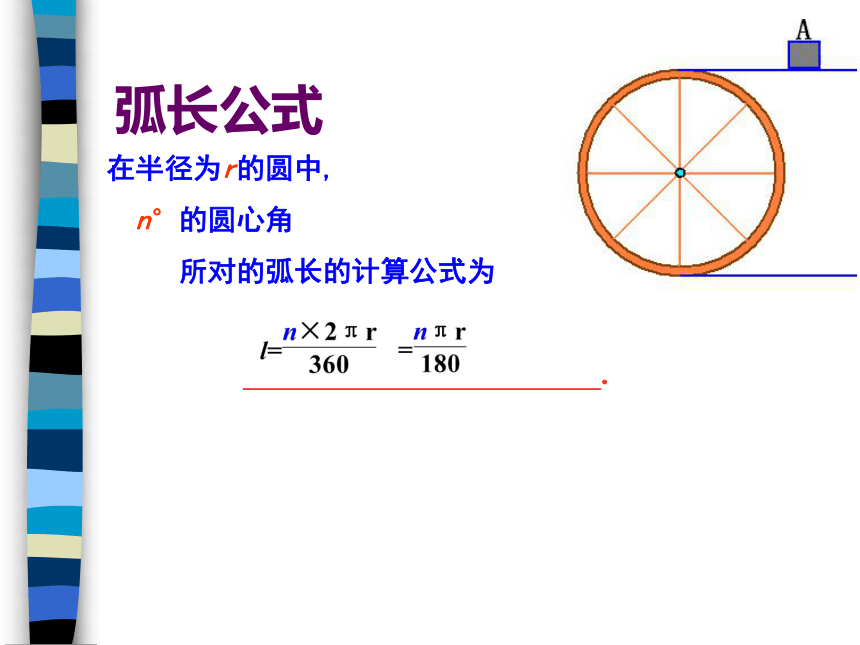
传送带上的物品A被传送 厘米；弧长公式2πr转动轮转2°,传送带上的物品A被传送 厘米；. . . . . . 在半径为r的圆中,
n°的圆心角
所对的弧长的计算公式为
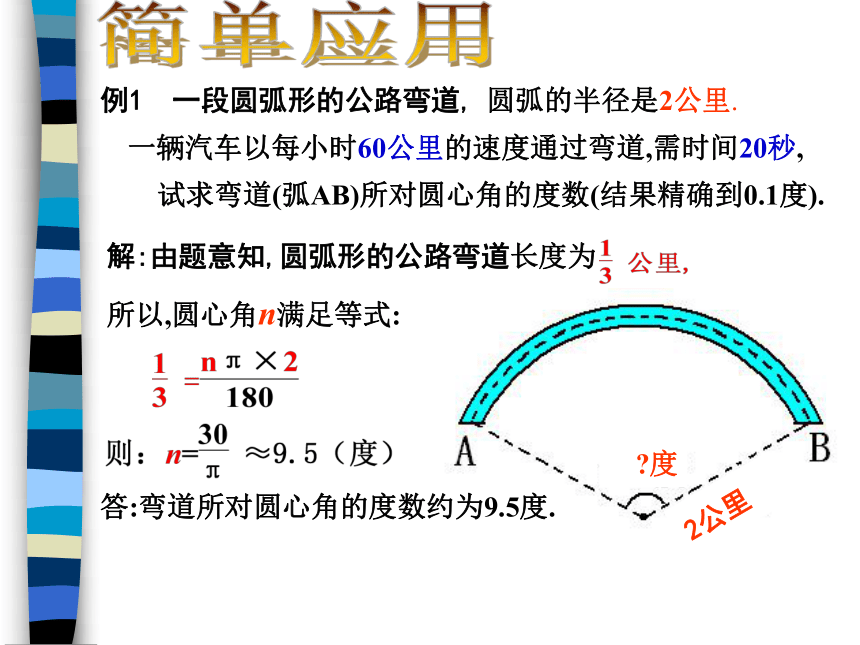
.弧长公式例1 一段圆弧形的公路弯道,简单应用解:由题意知,圆弧形的公路弯道长度为2公里?度试求弯道(弧AB)所对圆心角的度数(结果精确到0.1度).一辆汽车以每小时60公里的速度通过弯道,需时间20秒, 圆弧的半径是2公里.所以,圆心角n满足等式:答:弯道所对圆心角的度数约为9.5度.趣味题在一块空旷的草地上有一根柱子,柱子上拴着一条长3m的绳子,
绳子的另一端拴着一只狗.问:这只狗的最大活动区域有多大?如果这只狗只能绕柱子转过 ,
那么它的最大活动
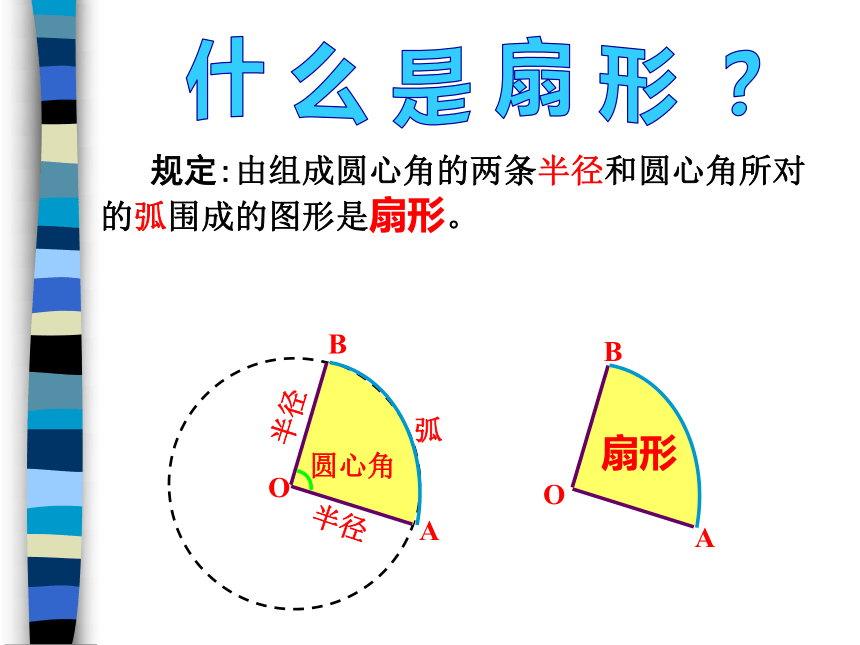
区域有多大?n°角什 么 是 扇 形 ？ 规定:由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。OBA圆心角如 何 求 扇 形 的 面 积 ？想 一 想 ：圆心角是 的扇形面积是多少？360018009002700发现：增大。圆心角是10的扇形面积是圆面积的 圆心角是n0的扇形面积是圆面积的 结 论 ：若字母 S 表示扇形的面积，n表示圆心角度数，r 表示圆半径，
则计算扇形面积的公式为：. . . . . . no小 练 习CCB例 题 剖 析例2 求图中红色部分的面积。（单位：cm， π 取3.14，结果保留整数）解二 （间接求法） S扇形＝S大圆－S小扇形r=15cm ,n=360o－72o=288o≈565（cm2）解一 （直接用扇形面积公式计算）例 题 剖 析例3:如图,有一把折扇和一把团扇.解:设折扇的骨柄长为2r，而S团扇＝πr2∴两把扇子扇面的面积一样大；答：两把扇子扇面的面积一样大。已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度
是骨柄长的一半,问那一把扇子扇面的面积大? 由于折扇扇面面积为两个扇形面积之 ，差1200折扇张开的角度为120O,当圆心角确定时，弧长与圆的 有关扇形的面积与圆的 有关周长扇形的面积弧长与面积探究:
当圆心角确定时,S扇形与l弧之间满足的数量关系？观察下列两个公式:拓展与运用1.扇形AOB的半径为1米, ∠AOB=45°,
求 的长和扇形AOB的面积？（结果保留π）拓展与运用2.某引水工程的主干线输水管的半径为1米，如果水管截面中水面面积如图所示，其中∠AOB=45°,已知，设计每秒流量为12.4米3，试求输水管中水的流速应达到每秒几米？可设输水管中水的流速应达到每秒x米,所以，x=4.00（米）答：该输水管中水的
流速应达到每秒4.00米再见