5.6三角形的中位线

课件19张PPT。链接说明:1.在第四张幻灯片上的”区分”有个链接;
2.在第五张幻灯片上”方法一、二、三、四”上有链接5.6三角形的中位线义务教育课程标准实验教科书　
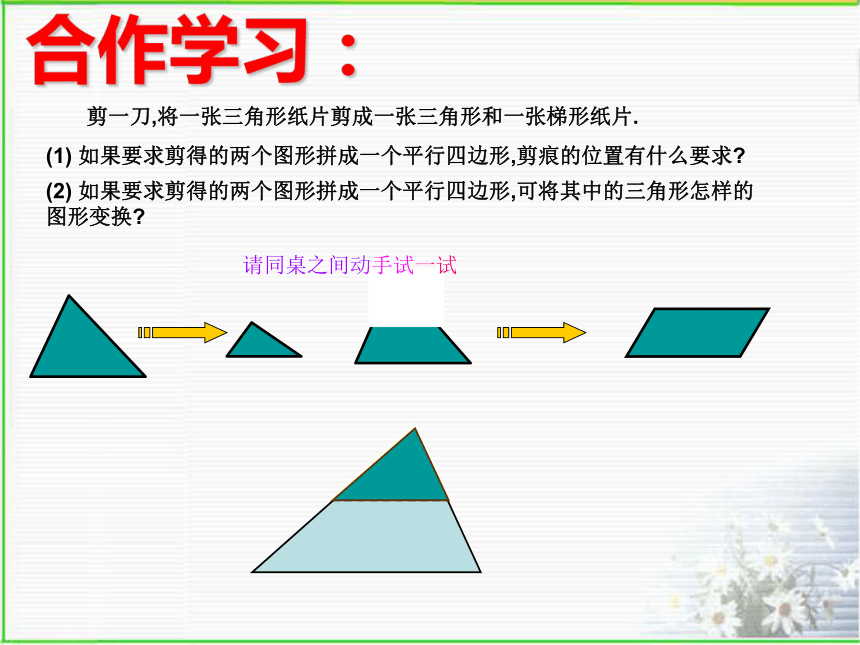
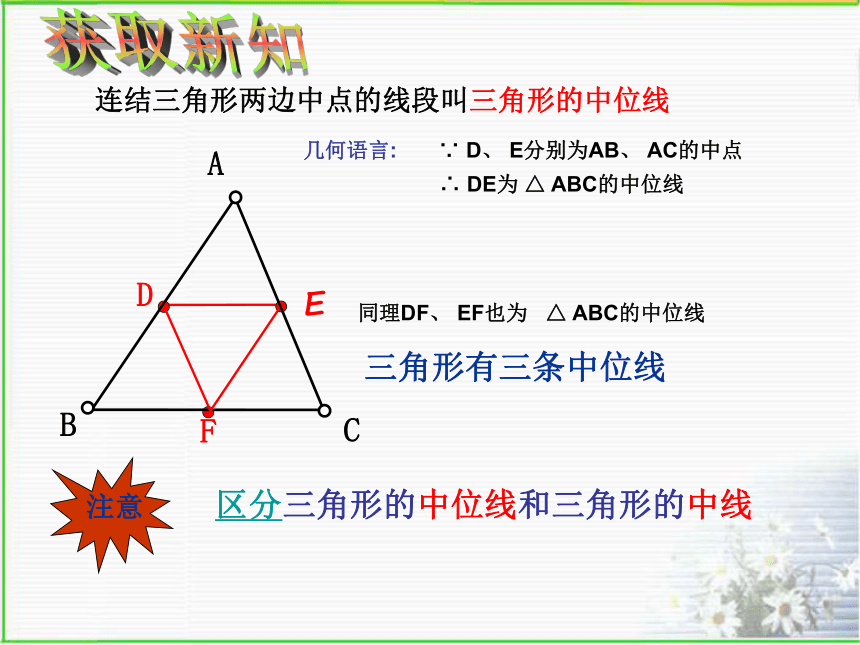
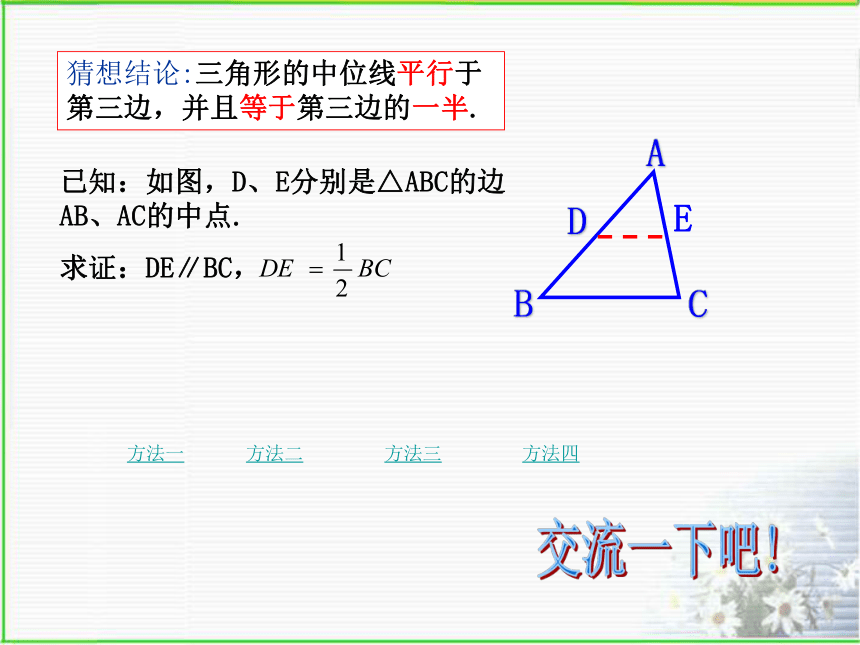
浙江版《数学》八年级下册5.6三角形的中位线合作学习：剪一刀,将一张三角形纸片剪成一张三角形和一张梯形纸片.(1) 如果要求剪得的两个图形拼成一个平行四边形,剪痕的位置有什么要求?(2) 如果要求剪得的两个图形拼成一个平行四边形,可将其中的三角形怎样的 图形变换?请同桌之间动手试一试获取新知连结三角形两边中点的线段叫三角形的中位线三角形有三条中位线区分三角形的中位线和三角形的中线 EDF几何语言:∵ D、 E分别为AB、 AC的中点∴ DE为 △ ABC的中位线同理DF、 EF也为 △ ABC的中位线猜想:中位线DE与第三边BC有什么位置关系? 有什么大小关系?猜想结论:三角形的中位线平行于第三边，并且等于第三边的一半.已知：如图，D、E分别是△ABC的边AB、AC的中点.
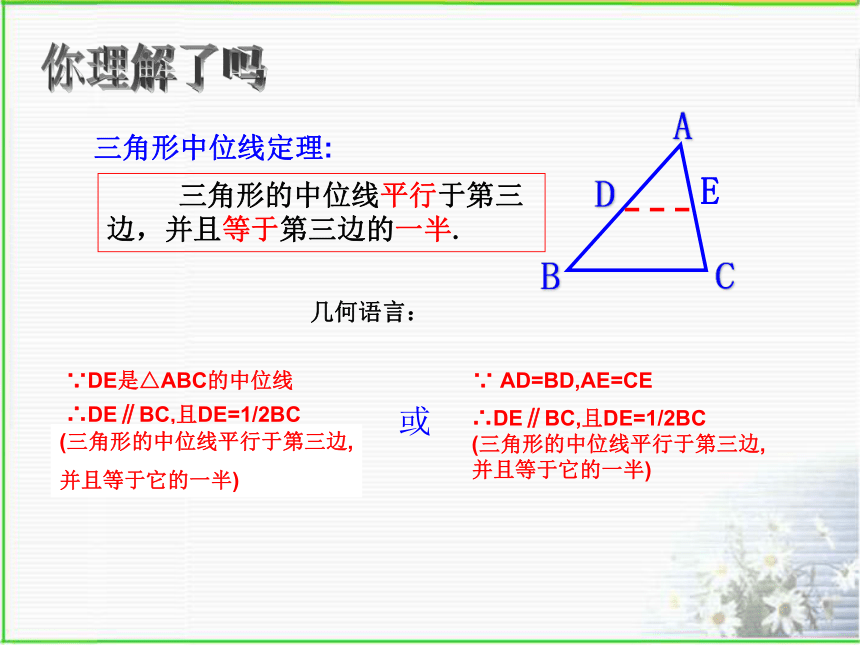
求证：DE∥BC，交流一下吧!你理解了吗 三角形的中位线平行于第三边，并且等于第三边的一半.三角形中位线定理:几何语言：∵DE是△ABC的中位线(三角形的中位线平行于第三边,
并且等于它的一半)或∵ AD=BD,AE=CE∴DE∥BC,且DE=1/2BC
(三角形的中位线平行于第三边,
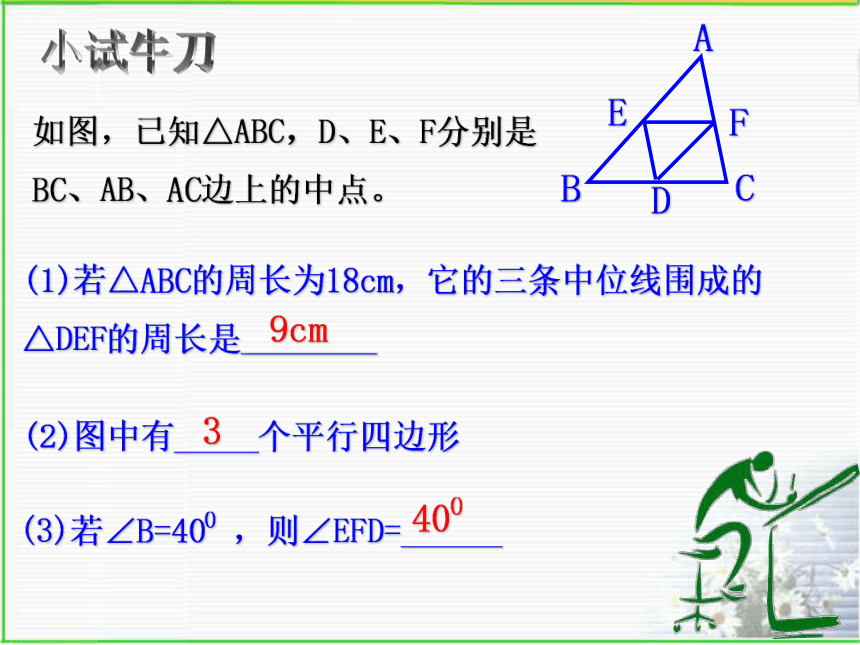
并且等于它的一半)(3)若∠B=40O ，则∠EFD=______如图，已知△ABC，D、E、F分别是BC、AB、AC边上的中点。(1)若△ABC的周长为18cm，它的三条中位线围成的△DEF的周长是________4009cm(2)图中有_____个平行四边形3小试牛刀 要测量B,C两地的距离,小明想出一个方法:在池塘外取点A,得到线段AB,AC.并取AB,AC的中点D,E,连结DE.只要测出DE的长,就可以求得B,C两地的距离.你认为这个方法正确吗?请说明理由.你能告诉大家吗?正确。理由：∵DE是△ABC的中位线(三角形的中位线平行于第三边,
并且等于它的一半)所以只要量出D,E两地的距离,就可以求出B,C两地的距离了.例1:已知：如图，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点.求证：四边形EFGH是平行四边形.新知应用证明:如图,连结AC∵EF是△ABC的中位线,∴EF∥1/2AC且EF=1/2AC(三角形的中位线平行于第三边,
并且等于它的一半)同理,HG ∥1/2AC且HG=1/2AC∴EF ∥HG且EF=HG∴四边形EFGH是平行四边形(一组对边平行且相等的四边形是平行四边形)由例题你能得到什么结论吗?顺次连接四边形各边中点的线段组成一个平行四边形.例2:已知：如图，△ABC是锐角三角形。分别以AB，AC为边向外侧作等边三角形ABM和等边三角形CAN。D，E，F分别是MB，BC，CN的中点，连结DE，EF。
求证：DE=EF你能行!1.已知: 如图,DE,EF是⊿ABC的两条中位线。
求证：四边形BFED是平行四边形。考考你!2、如图,DE是△ABC的中位线,AF是BC边上的中线,DE和AF交于点O.求证:DE与AF互相平分.考考你!体会.分享说能出你这节课的收获和体验让大家与你分享吗？谢谢!ABCDEAD是△ABC的中线DE是△ABC的中位线要 注 意 区 分 呀 !返回CEDFBA返回
你还有不同的方法加以证明吗?证明：如图，以点E为旋转中心，把⊿ADE绕点E，按顺时针方向旋转180゜，得到⊿CFE，则D，E，F同在一直线上DE=EF，且⊿ADE≌⊿CFE。∴∠ADE=∠F，AD=CF，∴AB∥CF。又∵BD=AD=CF，∴四边形BCFD是平行四边形（一组对边平行且相等的四边形是平行四边形），∴DF∥BC（根据什么？），(平行四边形的对边互相平行)CEDFBA返回ABCEDF返回ACEDFGB返回