九年级数学上册3.1圆（1）课件

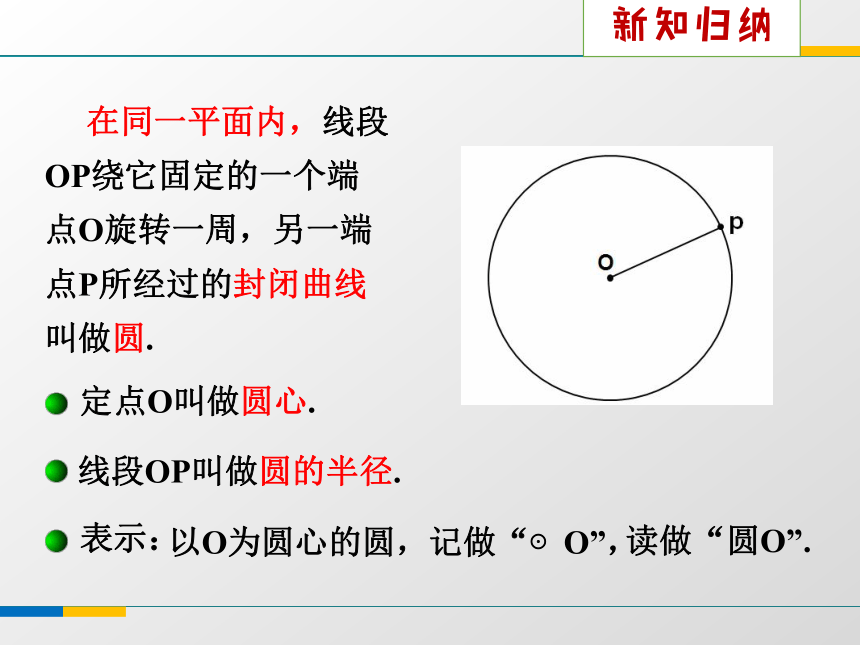
课件20张PPT。3.1 圆（1）圆是生活中常见的图形，许多物体都给我们以圆的形象.探究新知月亮请在白纸上画一个半径为2cm的圆． 若要在平坦的操场上画一个半径为3m的圆,你有什么办法?画一画 在同一平面内，线段OP绕它固定的一个端点O旋转一周，另一端点P所经过的封闭曲线叫做圆.定点O叫做圆心.线段OP叫做圆的半径.新知归纳圆上任意两点间的部分叫做圆弧, 简称弧.直径将圆分成两部分, 每一部分都叫做半圆
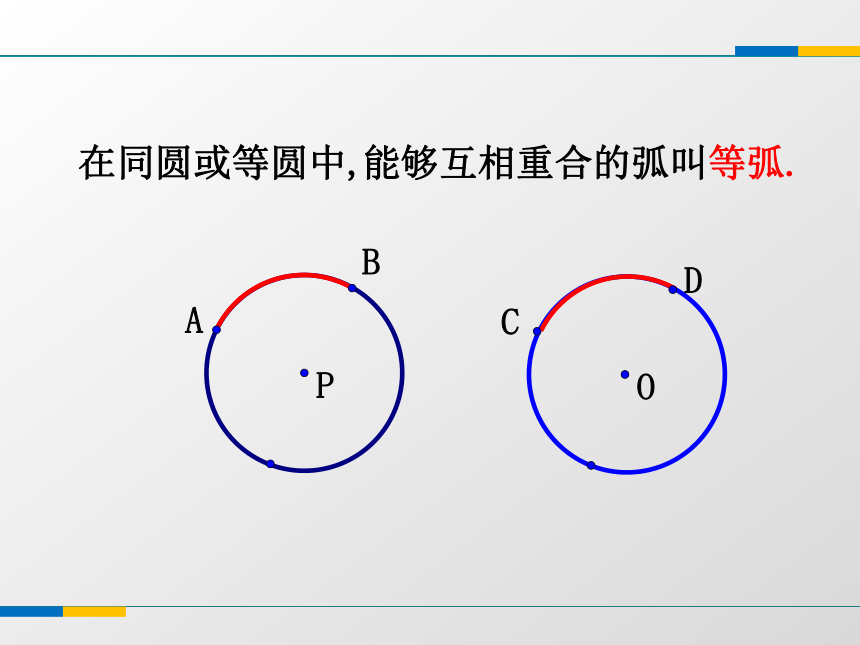
(如弧ABC).连接圆上任意两点间的线段叫做弦 (如弦AB).经过圆心的弦叫做直径(如直径AC). 请将自己所画的圆与同伴所画的圆进行比较， 它们是否能够完全重合？并思考什么情况下两个圆能够完全重合？半径相等的两个圆叫做等圆.POABCD能够互相重合的弧叫等弧.在同圆或等圆中,1、请写出图中所有的弦；2、请任选一条弦，写出这条弦所对的弧；做一做OABC ⊙O的半径为r =3m.若A，B，C三位同学分别站在如图所示的位置.A，B，C三点与圆的位置关系是什么？继续探究O 如图，设⊙O的半径为r，点到圆心的距离为d.d＝r若点A在圆上，则：若点C在圆外，则：d＞r若点B在圆内，则：d＜rABC如图，设⊙O的半径为r，A点在圆内，B点在圆上，
C点在圆外，那么OA＜r， OB＝r， OC＞r．反过来也成立，即点的位置可以确定该点到圆心的距离与半径的关系， 反过来，已知点到圆心的距离与半径的关系可以确定该点到圆的位置关系.已知⊙O的面积为25π.（1）若PO=5.5，则点P在 ；（2）若PO=4，则点P在 ；（3）若PO= ，则点P在圆上.圆外圆内5做一做例1 如图，在A地正北80m的Ｂ处有一幢民房，正西100m的C处有一变电设施，在BC的中点D处是一古建筑.因施工需要，必须在A处进行一次爆破.为使民房、变电设施、古建筑都不遭到破坏，问爆破影响面的半径应控制在什么范围内？例题探究解：连接AD
由题意我们可知答：爆破影响面的半径应小于课堂练习1、在直角三角形ABC中，∠C=Rt∠，AC=3cm，AB=5cm. 若以点C为圆心，画一个半径为3cm的圆，试判断点A，点B和⊙C的相互位置关系.2、如图，已知矩形ABCD的边
AB=3厘米，AD=4厘米.
（1）以点A为圆心，4厘米为半径作圆A，则点B、C、D与圆A的位置关系如何？
（2）若以A点为圆心作圆A，使B、C、D三点中至少有一个点在圆内，且至少有一个点在圆外，则圆A的半径r的取值范围是什么？3、如图，在A岛附近，半径约250km的范围内是一暗礁区，往北300km有一灯塔Ｂ，往西400km有一灯塔C.现有一渔船沿CB航行，问渔船会进入暗礁区吗？D课堂小结1、圆、弦和弧的概念及其表示方法； 2、同一平面内点与圆的位置关系及其判定.1. 课内练习
2. 课后作业题A组课后作业