九年级数学上册3.3垂径定理(1)课件
图片预览




文档简介
课件19张PPT。3.3 垂径定理(1)1.圆是什么对称图形?你是如何验证的?(1)圆是中心对称图形,圆心是它的对称中心;
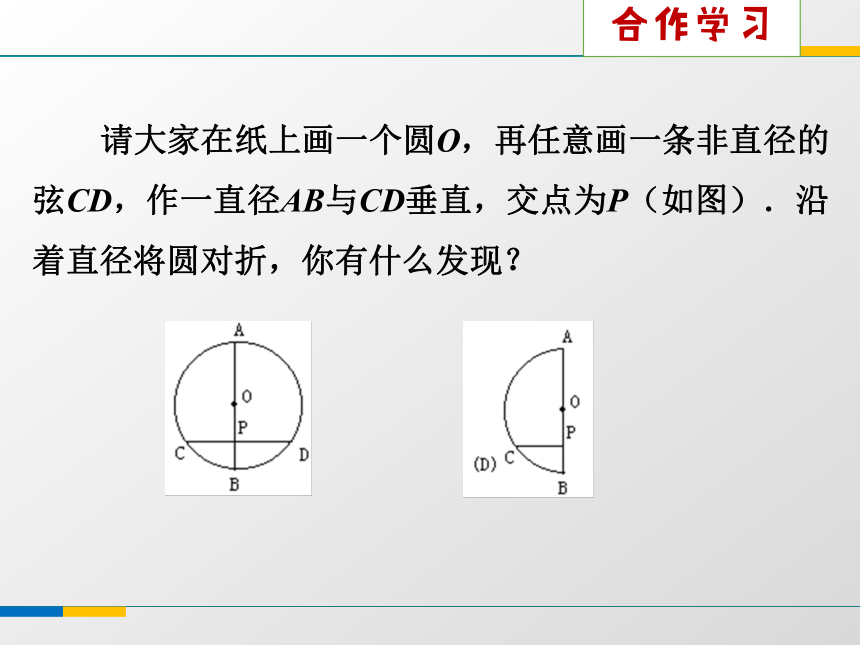
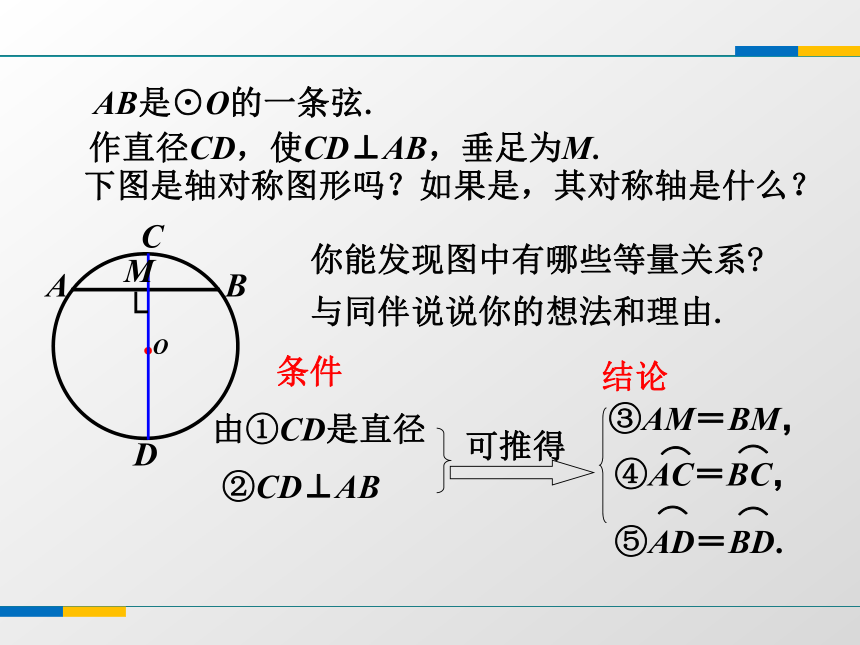
(2)圆是轴对称图形,经过圆心的直线是它的对称轴.知识探究 2.圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?你是如何验证的?1.圆既是中心对称图形,又是轴对称图形. 2.圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.3.可利用折叠的方法即可解决上述问题. 请大家在纸上画一个圆O,再任意画一条非直径的弦CD,作一直径AB与CD垂直,交点为P(如图).沿着直径将圆对折,你有什么发现?合作学习③AM=BM,AB是⊙O的一条弦.你能发现图中有哪些等量关系?
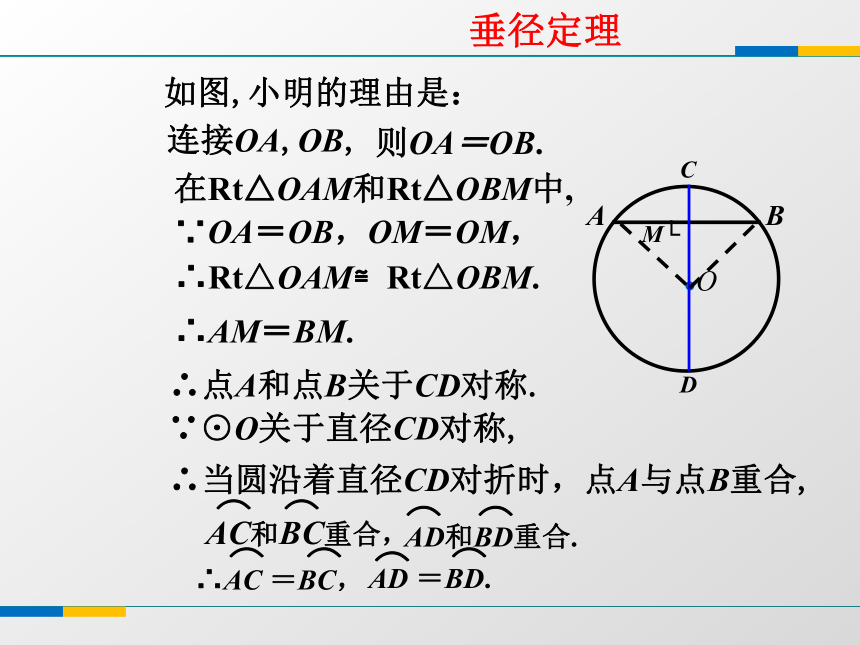
与同伴说说你的想法和理由.作直径CD,使CD⊥AB,垂足为M.下图是轴对称图形吗?如果是,其对称轴是什么? 由①CD是直径②CD⊥AB条件结论垂径定理如图,小明的理由是:连接OA,OB,则OA=OB.在Rt△OAM和Rt△OBM中,∵OA=OB,OM=OM,∴Rt△OAM≌Rt△OBM.∴AM=BM.∴点A和点B关于CD对称.∵⊙O关于直径CD对称,∴当圆沿着直径CD对折时,点A与点B重合,定理:垂直于弦的直径平分弦, 并且平分弦所对的两条弧.提示:
垂径定理是圆中一个重要的结论,三种形式要相互转化,形成整体,才能运用自如.CD⊥AB,如图∵ CD是直径,∴AM = BM,归纳总结分一条弧成相等的两条弧的点,叫做这条弧的中点.E1. 连结AB;作法:例题探究例2、一条排水管的截面如图所示. 已知排水管的半径OB=10,水面宽AB=16. 求截面圆心O到水面的距离.DC1088解: 作OC⊥AB于C,
由垂径定理得:
AC=BC=AB/2=0.5×16=8
由勾股定理得:
答: 截面圆心O到水面的距离为6.圆心到圆的一条弦的距离叫做弦心距.例如, 上图中, OC的长就是弦AB的弦心距. 1、下列图形中,哪些能使用垂径定理,为什么?小试身手2、如图,以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C、D.AC与BD相等吗?为什么?相等利用垂径定理C课堂练习2. 如图,OE⊥AB于E,若⊙O的半径为10cm, OE=6cm, 则AB= cm.·OABE解:连接OA. ∵ OE⊥AB,∴∴ AB=2AE=16cm.∴∠OEA=90°.3. 如图,⊙O直径为10,弦AB的长为8,点P在AB上运动. 则OP的取值范围是_________________.3≤OP≤54. 如图,CD是⊙O的直径,弦AB⊥CD于E,CE=1,AB=10,求直径CD的长.解:连接OA.∵ CD是直径,OE⊥AB,设OA=x,则OE=x-1,由勾股定理得x2=52+(x-1)2 .解得:x=13.∴ OA=13.∴ CD=2OA=26.即直径CD的长为26.∴ AE= AB=5. 通过本节课的学习,你对圆的性质有哪些进一步的认识? 课堂小结在 ⊙O中,弦AB∥CD.则弧AB与弧CD相等吗? 结论: 圆的两条平行弦所夹的弧相等.1.两弦在圆心的同侧
挑战自我
(2)圆是轴对称图形,经过圆心的直线是它的对称轴.知识探究 2.圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?你是如何验证的?1.圆既是中心对称图形,又是轴对称图形. 2.圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.3.可利用折叠的方法即可解决上述问题. 请大家在纸上画一个圆O,再任意画一条非直径的弦CD,作一直径AB与CD垂直,交点为P(如图).沿着直径将圆对折,你有什么发现?合作学习③AM=BM,AB是⊙O的一条弦.你能发现图中有哪些等量关系?
与同伴说说你的想法和理由.作直径CD,使CD⊥AB,垂足为M.下图是轴对称图形吗?如果是,其对称轴是什么? 由①CD是直径②CD⊥AB条件结论垂径定理如图,小明的理由是:连接OA,OB,则OA=OB.在Rt△OAM和Rt△OBM中,∵OA=OB,OM=OM,∴Rt△OAM≌Rt△OBM.∴AM=BM.∴点A和点B关于CD对称.∵⊙O关于直径CD对称,∴当圆沿着直径CD对折时,点A与点B重合,定理:垂直于弦的直径平分弦, 并且平分弦所对的两条弧.提示:
垂径定理是圆中一个重要的结论,三种形式要相互转化,形成整体,才能运用自如.CD⊥AB,如图∵ CD是直径,∴AM = BM,归纳总结分一条弧成相等的两条弧的点,叫做这条弧的中点.E1. 连结AB;作法:例题探究例2、一条排水管的截面如图所示. 已知排水管的半径OB=10,水面宽AB=16. 求截面圆心O到水面的距离.DC1088解: 作OC⊥AB于C,
由垂径定理得:
AC=BC=AB/2=0.5×16=8
由勾股定理得:
答: 截面圆心O到水面的距离为6.圆心到圆的一条弦的距离叫做弦心距.例如, 上图中, OC的长就是弦AB的弦心距. 1、下列图形中,哪些能使用垂径定理,为什么?小试身手2、如图,以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C、D.AC与BD相等吗?为什么?相等利用垂径定理C课堂练习2. 如图,OE⊥AB于E,若⊙O的半径为10cm, OE=6cm, 则AB= cm.·OABE解:连接OA. ∵ OE⊥AB,∴∴ AB=2AE=16cm.∴∠OEA=90°.3. 如图,⊙O直径为10,弦AB的长为8,点P在AB上运动. 则OP的取值范围是_________________.3≤OP≤54. 如图,CD是⊙O的直径,弦AB⊥CD于E,CE=1,AB=10,求直径CD的长.解:连接OA.∵ CD是直径,OE⊥AB,设OA=x,则OE=x-1,由勾股定理得x2=52+(x-1)2 .解得:x=13.∴ OA=13.∴ CD=2OA=26.即直径CD的长为26.∴ AE= AB=5. 通过本节课的学习,你对圆的性质有哪些进一步的认识? 课堂小结在 ⊙O中,弦AB∥CD.则弧AB与弧CD相等吗? 结论: 圆的两条平行弦所夹的弧相等.1.两弦在圆心的同侧
挑战自我
同课章节目录
