6.1几何图形 同步训练

6.1几何图形
　
一．选择题（共8小题）
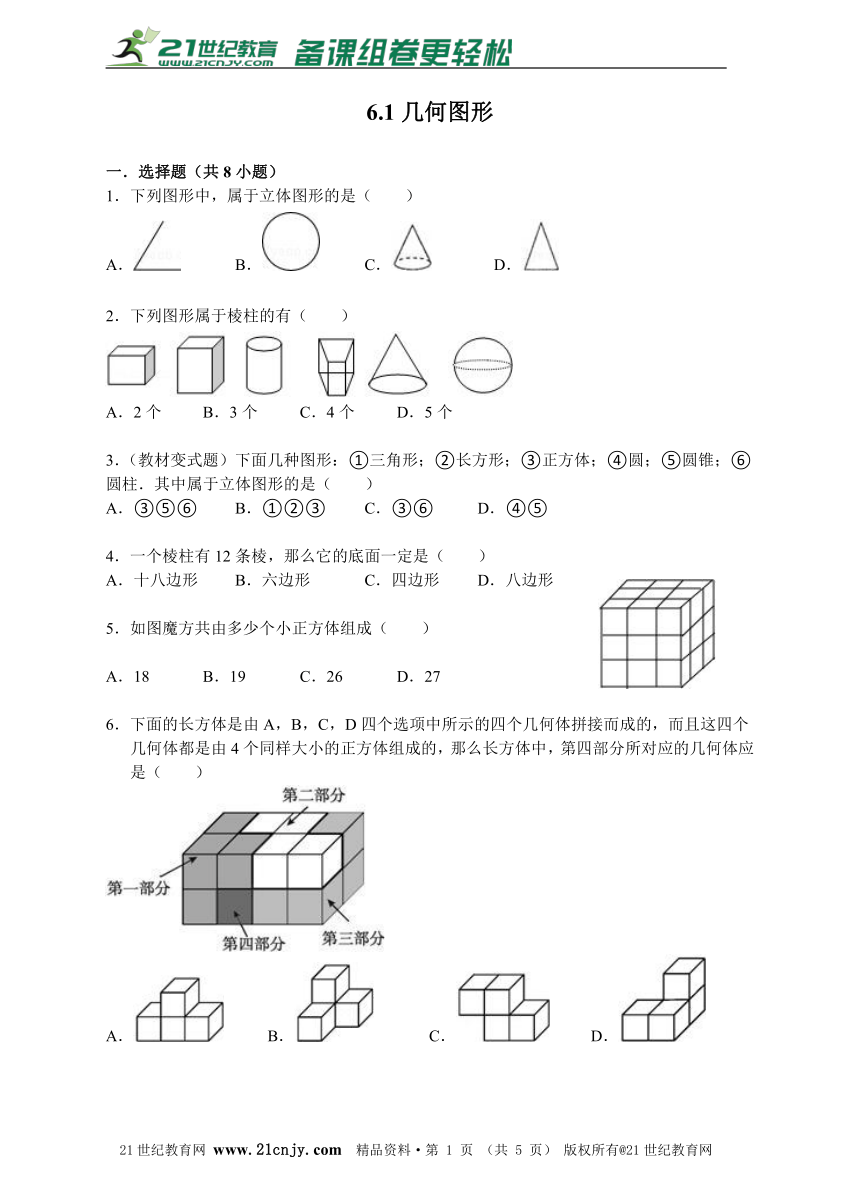
1．下列图形中，属于立体图形的是（　　）
A． B． C． D．
2．下列图形属于棱柱的有（　　）
A．2个 B．3个 C．4个 D．5个
3．（教材变式题）下面几种图形：①三角形；②长方形；③正方体；④圆；⑤圆锥；⑥圆柱．其中属于立体图形的是（　　）21世纪教育网版权所有
A．③⑤⑥ B．①②③ C．③⑥ D．④⑤
4．一个棱柱有12条棱，那么它的底面一定是（　　）
A．十八边形 B．六边形 C．四边形 D．八边形
5．如图魔方共由多少个小正方体组成（　　）
A．18 B．19 C．26 D．27
6．下面的长方体是由A，B，C，D四个选项中所示的四个几何体拼接而成的，而且这四个几何体都是由4个同样大小的正方体组成的，那么长方体中，第四部分所对应的几何体应是（　　）21·cn·jy·com
A． B． C． D．
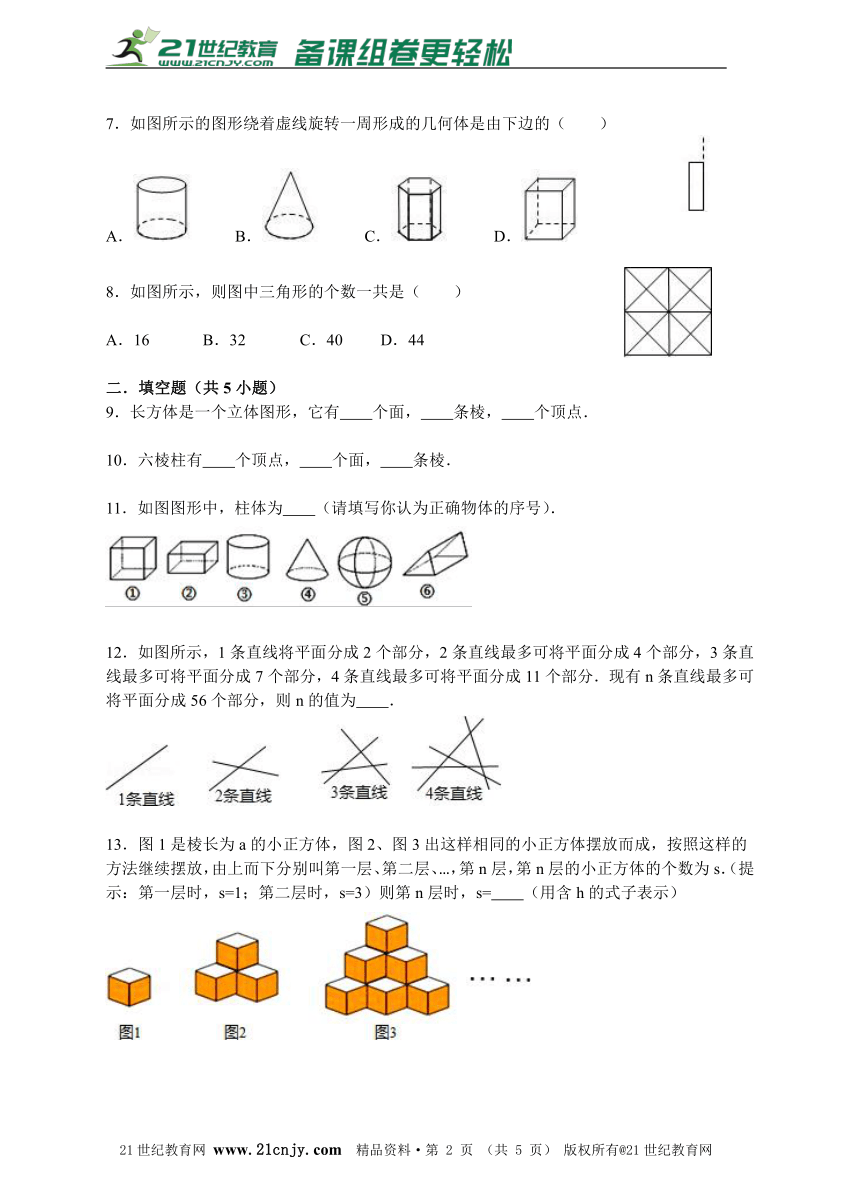
7．如图所示的图形绕着虚线旋转一周形成的几何体是由下边的（　　）
A． B． C． D．
8．如图所示，则图中三角形的个数一共是（　　）
A．16 B．32 C．40 D．44
　
二．填空题（共5小题）
9．长方体是一个立体图形，它有　　个面，　　条棱，　　个顶点．
10．六棱柱有　　个顶点，　　个面，　　条棱．
11．如图图形中，柱体为　　（请填写你认为正确物体的序号）．
12．如图所示，1条直线将平面分成2个部分，2条直线最多可将平面分成4个部分，3条直线最多可将平面分成7个部分，4条直线最多可将平面分成11个部分．现有n条直线最多可将平面分成56个部分，则n的值为　　．www.21-cn-jy.com
13．图1是棱长为a的小正方体，图2、图3出这样相同的小正方体摆放而成，按照这样的方法继续摆放，由上而下分别叫第一层、第二层、…，第n层，第n层的小正方体的个数为s．（提示：第一层时，s=1；第二层时，s=3）则第n层时，s=　　（用含h的式子表示）
　
三．解答题（共3小题）
14．将下列几何体与它的名称连接起来．
15．如图，是一个几何体从正面、左面、上面看得到的平面图形，判断下面说法的正误（正确的在括号内划△，错误的在括号内划▲）21·世纪*教育网
（1）这是一个棱锥　　．
（2）这个几何体有4个面　　．
（3）这个几何体有5个顶点　　．
（4）这个几何体有8条棱　　．
（5）请你再说出一个正确的结论　　．
16．将一个正方体木块涂成红色，然后如图把它的棱三等分，再沿等分线把正方体切开，可以得到27个小正方体．观察并回答下列问题：2·1·c·n·j·y
（1）其中三面涂色的小正方体有　　个，两面涂色的小正方体有　　个，各面都没有涂色的小正方体有　　个；【来源：21·世纪·教育·网】
（2）如果将这个正方体的棱n等分，所得的小正方体中三面涂色的有　　个，各面都没有涂色的有　　个；
（3）如果要得到各面都没有涂色的小正方体100个，那么至少应该将此正方体的棱　　等分．
　

6.1几何图形
参考答案与试题解析
　
一．选择题（共8小题）
2．解：第一、二、四个几何体是棱柱，故选：B．　
3．解：根据以上分析：属于立体图形的是③正方体；⑤圆锥；⑥圆柱．故选A．
4．解：设该棱柱为n棱柱．根据题意得：3n=12．解得：n=4．
所以该棱柱为4棱柱．故选：C．
5．解：每一层小正方体有9个，共3层，小正方体的总数为：3×9=27，故选：D．
6．解：由几何体的图形可知，第四部分，看到的一个，后面三个，故选A．
7．解：结合图形特征可知，所围成的几何体是圆柱．故选A．
8．解：根据图形特点把图中三角形分类，单一的小三角形是16个；再数出由2个小三角形组成的三角形是16个；再数出由4个小三角形组成的三角形是8个；再数出由8个小三角形组成的三角形是4个．21教育网
故图中共有三角形个数为：16+16+8+4=44（个）．
答：图中三角形的个数一共是44个．故选D．
　
二．填空题（共5小题）
9．解：长方体有6个面，12条棱，8个顶点．故答案为：6，12，8．
11．解：柱体有①②③⑥．故答案是：①②③⑥．
12．解：依题意有n（n+1）+1=56，解得n1=﹣11（不合题意舍去），n2=10．
答：n的值为10．故答案为：10．
13．解：∵第1个图有1层，共1个小正方体，
第2个图有2层，第2层正方体的个数为1+2，
第3个图有3层，第3层正方体的个数为1+2+3，
∴第n层时，s=1+2+3+…+n=n（n+1）．故答案为：n（n+1）．
　
三．解答题（共3小题）
14．解：如图所示：
　
15．解：（1）这是一个棱锥△；
（2）这个几何体有4个面▲；
（3）这个几何体有5个顶点△；
（4）这个几何体有8条棱△；
（5）请你再说出一个正确的结论：底面是正方形，
故答案为：（1）△；（2）；（3）△；（4）△；（5）底面是正方形．
　
16．解：（1）如图②，把正方体的棱三等分，然后沿等分线把正方体切开，得到27个小正方体．观察其中三面被涂色的有8个，两面涂色的有12个； 各面都没有涂色的有1个，故答案为：8，12，1； 21cnjy.com
（2）根据正方体的棱三等分时三面被涂色的有8个，有1个是各个面都没有涂色的，
正方体的棱四等分时三面被涂色的有8个，有8个是各个面都没有涂色的，
∴正方体的棱n等分时三面被涂色的有8个，有（n﹣2）3个是各个面都没有涂色的，
故答案为：8，（n﹣2）3；