4.1探索确位置的方法同步练习

4.1探索确位置的方法同步练习
　
一．选择题（共9小题）
1．点A的位置如图所示，则关于点A的位置下列说法中正确的是（　　）
A．距点O4km处
B．北偏东40°方向上4km处
C．在点O北偏东50°方向上4km处
D．在点O北偏东40°方向上4km处
2．如图，是雷达探测器测得的结果，图中显示在点A，B，C，D，E，F处有目标出现，目标的表示方法为（r，α），其中，r表示目标与探测器的距离；α表示以正东为始边，逆时针旋转后的角度．例如，点A，D的位置表示为A（5，30°），D（4，240°）．用这种方法表示点B，C，E，F的位置，其中正确的是（　　）21世纪教育网版权所有
A．B（2，90°） B．C（2，120°） C．E（3，120°） D．F（4，210°）
3．以下是甲、乙、丙三人看地图时对四个坐标的描述：
甲：从学校向北直走500米，再向东直走100米可到图书馆．
乙：从学校向西直走300米，再向北直走200米可到邮局．
丙：邮局在火车站西200米处．
根据三人的描述，若从图书馆出发，判断下列哪一种走法，其终点是火车站（　　）
A．向南直走300米，再向西直走200米
B．向南直走300米，再向西直走100米
C．向南直走700米，再向西直走200米
D．向南直走700米，再向西直走600米
4．根据下列表述，能确定位置的是（　　）
A．红星电影院2排 B．北京市四环路
C．北偏东30° D．东经118°，北纬40°
5．如果7年2班记作（7，2），那么（8，4）表示（　　）
A．7年4班 B．4年7班 C．4年8班 D．8年4班
6．如图所示是某古塔周围的建筑平面示意图，这座古塔A的位置用（5，4）来表示，张旻同学由点B出发到点A，他的路径表示错误的是（　　）21·cn·jy·com
A．（2，2）→（2，4）→（5，4） B．（2，2）→（2，4）→（4，5）
C．（2，2）→（4，2）→（4，4）→（5，4） D．（2，2）→（2，3）→（5，3）→（5，4）【来源：21cnj*y.co*m】
7．如图是田媛同学画的一张脸，若用（2，5）表示左眼A的位置，则右眼B的位置可表示为（　　）
A．（5，6） B．（6，5） C．（5，5） D．（6，6）
8．将正整数按如图所示的规律排列下去，若有序实数对（n，m）表示第n排，从左到右第m个数，如（4，2）表示9，则表示58的有序数对是（　　）【版权所有：21教育】
A．（11，3） B．（3，11） C．（11，9） D．（9，11）
9．某校数学课外小组，在坐标纸上为学校的一块空地设计植树方案如下：第k棵树种植在点Pk（xk，yk）处，其中x1=1，y1=1，当k≥2时，，[a]表示非负实数a的整数部分，例如[2.6]=2，[0.2]=0．按此方案，第2010棵树种植点的坐标为（　　）
A．（5，2009） B．（6，2010） C．（5，401） D．（5，402）
　
二．填空题（共5小题）
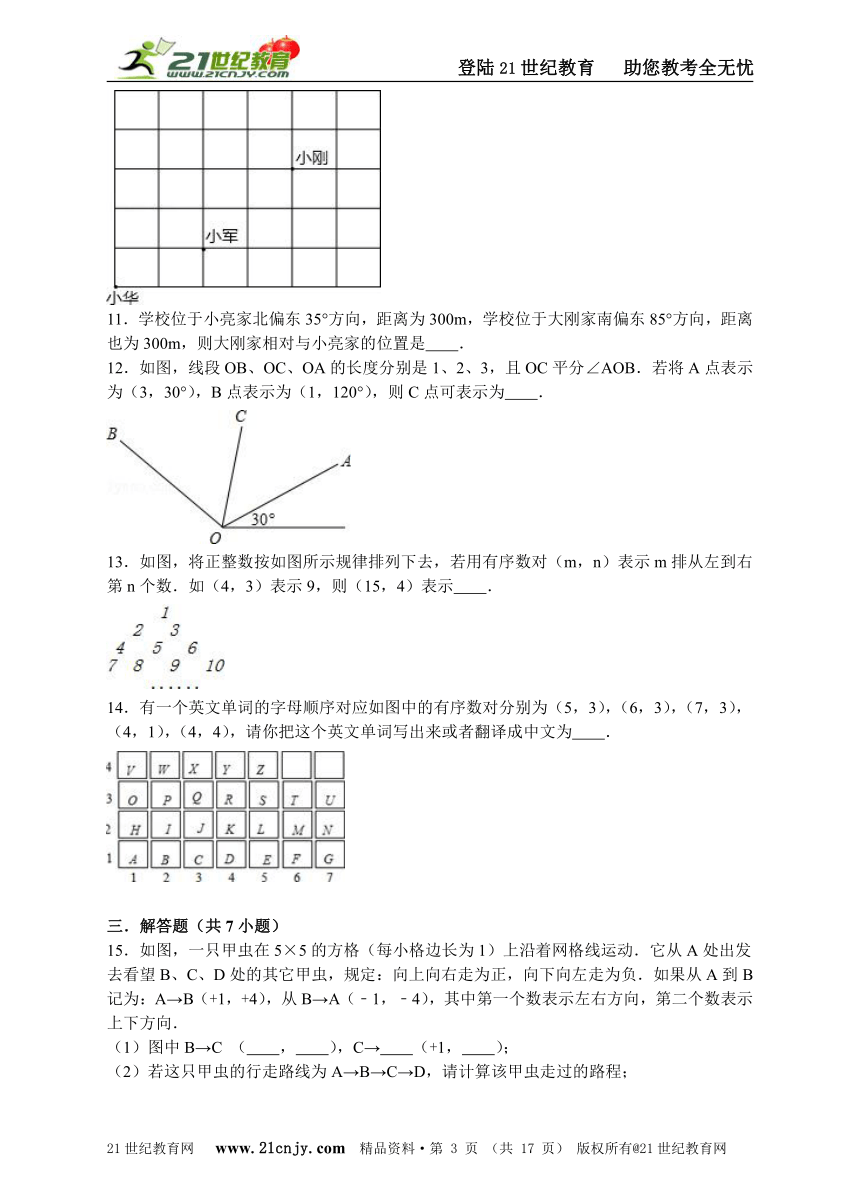
10．课间操时小华、小军、小刚的位置如图所示，小华对小刚说，如果我的位置用（0，0）表示，小军的位置用（2，1）表示，那么小刚的位置可以用坐标表示成　　．
11．学校位于小亮家北偏东35°方向，距离为300m，学校位于大刚家南偏东85°方向，距离也为300m，则大刚家相对与小亮家的位置是　　．21教育名师原创作品
12．如图，线段OB、OC、OA的长度分别是1、2、3，且OC平分∠AOB．若将A点表示为（3，30°），B点表示为（1，120°），则C点可表示为　　．21*cnjy*com
13．如图，将正整数按如图所示规律排列下去，若用有序数对（m，n）表示m排从左到右第n个数．如（4，3）表示9，则（15，4）表示　　．www-2-1-cnjy-com
14．有一个英文单词的字母顺序对应如图中的有序数对分别为（5，3），（6，3），（7，3），（4，1），（4，4），请你把这个英文单词写出来或者翻译成中文为　　．
　
三．解答题（共7小题）
15．如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动．它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走为正，向下向左走为负．如果从A到B记为：A→B（+1，+4），从B→A（﹣1，﹣4），其中第一个数表示左右方向，第二个数表示上下方向．
（1）图中B→C （　　，　　），C→　　（+1，　　）；
（2）若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程；
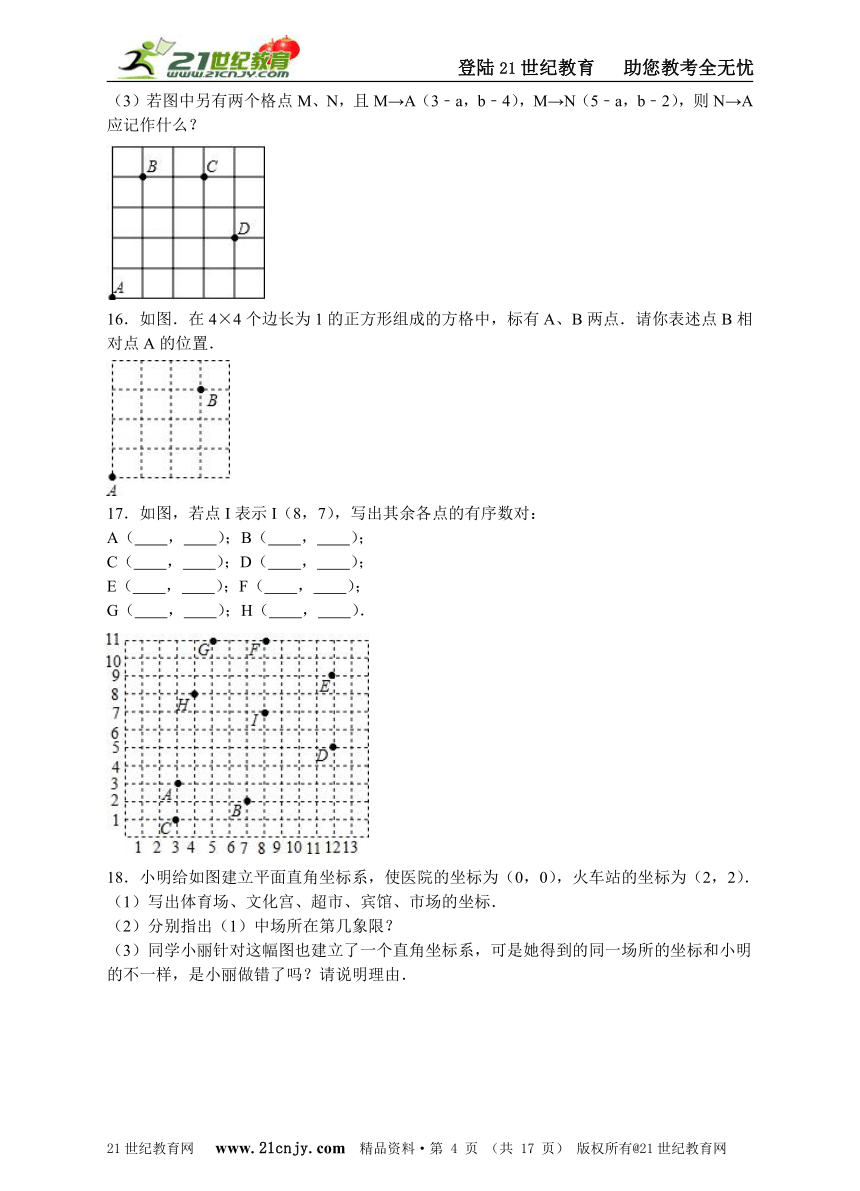
（3）若图中另有两个格点M、N，且M→A（3﹣a，b﹣4），M→N（5﹣a，b﹣2），则N→A应记作什么？
16．如图．在4×4个边长为1的正方形组成的方格中，标有A、B两点．请你表述点B相对点A的位置．
17．如图，若点I表示I（8，7），写出其余各点的有序数对：
A（　　，　　）；B（　　，　　）；
C（　　，　　）；D（　　，　　）；
E（　　，　　）；F（　　，　　）；
G（　　，　　）；H（　　，　　）．
18．小明给如图建立平面直角坐标系，使医院的坐标为（0，0），火车站的坐标为（2，2）．
（1）写出体育场、文化宫、超市、宾馆、市场的坐标．
（2）分别指出（1）中场所在第几象限？
（3）同学小丽针对这幅图也建立了一个直角坐标系，可是她得到的同一场所的坐标和小明的不一样，是小丽做错了吗？请说明理由．　　21*cnjy*com
19．某教室中，学生座位的平面图如图所示．
（1）说明王明和张强的位置；
（2）若用（3，2）表示第3排第2列的位置，那么（4，5）表示什么位置？王明和张强的位置可以怎样表示？
（3）在（2）的条件下，请说出（3，3）和（4，8）表示哪位同学的位置；
（4）在（2）的条件下，（3，4）和（4，3）表示的位置相同吗？一般地，若a≠b，（a，b）与（b，a）（1≤a≤5，1≤b≤8，a，b为整数）表示的位置相同吗？
20．如图的方格中有25个汉字，如四1表示“天”，请沿着以下路径去寻找你的礼物：
（1）一1→三2→二4→四3→五1
一
二
三
四
五
1
我
力
习
天
的
2
会
上
是
学
好
3
帅
就
更
棒
努
4
优
最
行
了
可
5
能
爱
秀
明
哥
（2）五3→二1→二3→一5→三4
（3）四5→四1→一2→三3→五2．
21．如图1，将射线OX按逆时针方向旋转β角，得到射线OY，如果点P为射线OY上的一点，且OP=a，那么我们规定用（a，β）表示点P在平面内的位置，并记为P（a，β），例如，图2中，如果OM=8，∠XOM=110°，那么点M在平面内的位置，记为M（8，110），根据图形，解答下面的问题：21教育网
（1）如图3，如果点N在平面内的位置记为N（6，30），那么ON=　　；∠XON=　　．
（2）如果点A、B在平面内的位置分别记为A（5，30），B（12，120），试求A、B两点之间的距离并画出图．
　

4.1探索确位置的方法同步练习
参考答案与试题解析
　
一．选择题（共9小题）
1．点A的位置如图所示，则关于点A的位置下列说法中正确的是（　　）
A．距点O4km处
B．北偏东40°方向上4km处
C．在点O北偏东50°方向上4km处
D．在点O北偏东40°方向上4km处
解：如图所示：点A在点O北偏东40°方向上4km处．
故选：D．
　
2．如图，是雷达探测器测得的结果，图中显示在点A，B，C，D，E，F处有目标出现，目标的表示方法为（r，α），其中，r表示目标与探测器的距离；α表示以正东为始边，逆时针旋转后的角度．例如，点A，D的位置表示为A（5，30°），D（4，240°）．用这种方法表示点B，C，E，F的位置，其中正确的是（　　）
A．B（2，90°） B．C（2，120°） C．E（3，120°） D．F（4，210°）
解：A、由题意可得：B（2，90°），故此选项正确；
B、由题意可得：C（3，120°），故此选项错误；
C、由题意可得：E（3，300°），故此选项错误；
D、由题意可得：F（5，210°），故此选项错误；
故选：A．
　
3．以下是甲、乙、丙三人看地图时对四个坐标的描述：
甲：从学校向北直走500米，再向东直走100米可到图书馆．
乙：从学校向西直走300米，再向北直走200米可到邮局．
丙：邮局在火车站西200米处．
根据三人的描述，若从图书馆出发，判断下列哪一种走法，其终点是火车站（　　）
A．向南直走300米，再向西直走200米
B．向南直走300米，再向西直走100米
C．向南直走700米，再向西直走200米
D．向南直走700米，再向西直走600米
解：如图，以学校为坐标原点画出直角坐标系，1个单位长表示100m，
从图书馆出发，向南直走300米，再向西直走200米可到火车站．
故选A．
　
4．根据下列表述，能确定位置的是（　　）
A．红星电影院2排 B．北京市四环路
C．北偏东30° D．东经118°，北纬40°
解：在平面内，点的位置是由一对有序实数确定的，只有D能确定一个位置，
故选：D．
　
5．如果7年2班记作（7，2），那么（8，4）表示（　　）
A．7年4班 B．4年7班 C．4年8班 D．8年4班
解：∵7年2班记作（7，2），
∴（8，4）表示8年4班，
故选：D．
　
6．如图所示是某古塔周围的建筑平面示意图，这座古塔A的位置用（5，4）来表示，张旻同学由点B出发到点A，他的路径表示错误的是（　　）www.21-cn-jy.com
A．（2，2）→（2，4）→（5，4） B．（2，2）→（2，4）→（4，5）
C．（2，2）→（4，2）→（4，4）→（5，4） D．（2，2）→（2，3）→（5，3）→（5，4）
解：A、由图象可知（2，2）→（2，4）→（5，4）到达点A正确．
B、由图象可知（2，2）→（2，4）→（4，5）不能到达点A，错误．
C、由图象可知（2，2）→（4，2）→（4，4）→（5，4）到达点A正确．
D、由图象可知2，2）→（2，3）→（5，3）→（5，4）到达点A正确．
故选B．
　
7．如图是田媛同学画的一张脸，若用（2，5）表示左眼A的位置，则右眼B的位置可表示为（　　）
A．（5，6） B．（6，5） C．（5，5） D．（6，6）
解：右眼B的位置可表示为（6，5），
故选：B．
　
8．将正整数按如图所示的规律排列下去，若有序实数对（n，m）表示第n排，从左到右第m个数，如（4，2）表示9，则表示58的有序数对是（　　）
A．（11，3） B．（3，11） C．（11，9） D．（9，11）
解：根据图中所揭示的规律可知，1+2+3+4+5+6+7+8+9+10=55，所以58在第11排；偶数排从左到右由大到小，奇数排从左到右由小到大，所以58应该在11排的从左到右第3个数．
故选A．
　
9．某校数学课外小组，在坐标纸上为学校的一块空地设计植树方案如下：第k棵树种植在点Pk（xk，yk）处，其中x1=1，y1=1，当k≥2时，，[a]表示非负实数a的整数部分，例如[2.6]=2，[0.2]=0．按此方案，第2010棵树种植点的坐标为（　　）
A．（5，2009） B．（6，2010） C．（5，401） D．（5，402）
解：根据题意，x1=1，
x2﹣x1=1﹣5[]+5[]，
x3﹣x2=1﹣5[]+5[]，
x4﹣x3=1﹣5[]+5[]，
…
xk﹣xk﹣1=1﹣5[]+5[]，
∴x1+（x2﹣x1）+（x3﹣x2）+（x4﹣x3）+…+（xk﹣xk﹣1），
=1+（1﹣5[]+5[]）+（1﹣5[]+5[]）+（1﹣5[]+5[]）+…+（1﹣5[]+5[]），
∴xk=k﹣5[]，
当k=2010时，x2010=2010﹣5[]=2010﹣5×401=5，
y1=1，
y2﹣y1=[]﹣[]，
y3﹣y2=[]﹣[]，
y4﹣y3=[]﹣[]，
…
yk﹣yk﹣1=[]﹣[]，
∴yk=1+[]，
当k=2010时，y2010=1+[]=1+401=402，
∴第2010棵树种植点的坐标为（5，402）．
故选D．
　
二．填空题（共5小题）
10．课间操时小华、小军、小刚的位置如图所示，小华对小刚说，如果我的位置用（0，0）表示，小军的位置用（2，1）表示，那么小刚的位置可以用坐标表示成　（4，3）　．
解：如图，小刚的位置可以用坐标表示成（4，3）．
故答案为（4，3）．
　
11．学校位于小亮家北偏东35°方向，距离为300m，学校位于大刚家南偏东85°方向，距离也为300m，则大刚家相对与小亮家的位置是　北偏西25°方向，距离为300m　．
解：据分析可知：小亮家、大刚家和学校构成了一个等边三角形，所以大刚家相对与小亮家的位置是北偏西25°方向，距离为300m．21cnjy.com
故答案为北偏西25°方向，距离为300m．
　
12．如图，线段OB、OC、OA的长度分别是1、2、3，且OC平分∠AOB．若将A点表示为（3，30°），B点表示为（1，120°），则C点可表示为　（2，75°）　．
解：∵线段OB、OC、OA的长度分别是1、2、3，且OC平分∠AOB．若将A点表示为（3，30°），B点表示为（1，120°），
∴∠AOB=90°，∠AOC=45°，
则C点可表示为（2，75°）．
故答案为：（2，75°）．
　
13．如图，将正整数按如图所示规律排列下去，若用有序数对（m，n）表示m排从左到右第n个数．如（4，3）表示9，则（15，4）表示　109　．
解：前14排共有1+2+3+…+14=105个数，
所以第15排的第4个数为109，即（15，4）表示109．
故答案为109．
　
14．有一个英文单词的字母顺序对应如图中的有序数对分别为（5，3），（6，3），（7，3），（4，1），（4，4），请你把这个英文单词写出来或者翻译成中文为　study（学习）　．
解：由图形可知：（5，3）表示s；（6，3）表示t；（7，3）表示u；（4，1）表示d；（4，4）表示y．
∴这个英文单词为study，翻译成中文为学习．
故答案为：study（学习）．
　
三．解答题（共7小题）
15．如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动．它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走为正，向下向左走为负．如果从A到B记为：A→B（+1，+4），从B→A（﹣1，﹣4），其中第一个数表示左右方向，第二个数表示上下方向．
（1）图中B→C （　+2　，　0　），C→　D　（+1，　﹣2　）；
（2）若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程；
（3）若图中另有两个格点M、N，且M→A（3﹣a，b﹣4），M→N（5﹣a，b﹣2），则N→A应记作什么？
解：（1）∵向上向右走为正，向下向左走为负，
∴图中B→C （+2，0），C→D（+1，﹣2）；
故答案为：+2，0，D，﹣2．
（2）甲虫走过的路程为1+4+2+1+2=10
（3）∵M→A（3﹣a，b﹣4），M→N（5﹣a，b﹣2），
∴5﹣a﹣（3﹣a）=2，b﹣2﹣（b﹣4）=2，
∴点A向右走2个格点，向上走2个格点到点N，
∴N→A应记为（﹣2，﹣2）．
　
16．如图．在4×4个边长为1的正方形组成的方格中，标有A、B两点．请你表述点B相对点A的位置．
解：方法1：用有序实数对（a，b）表示．
比如：以点A为原点，水平方向为x轴，建立直角坐标系，则B（3，3）．
方法2：用方向和距离表示．
比如：B点位于A点的东北方向（北偏东45°等均可），距离A点3处．
　
17．如图，若点I表示I（8，7），写出其余各点的有序数对：
A（　3　，　3　）；B（　7　，　2　）；
C（　3　，　1　）；D（　12　，　5　）；
E（　12　，　9　）；F（　8　，　11　）；
G（　5　，　11　）；H（　4　，　8　）．
解：∵用点I表示I（8，7），
∴坐标轴的位置如图所示：
∴A（3，3）；B（7，2）；
C（3，1）；D（12，5）；
E（12，9）；F（8，11）；
G（5，11）；H（4，8）．
　
18．小明给如图建立平面直角坐标系，使医院的坐标为（0，0），火车站的坐标为（2，2）．
（1）写出体育场、文化宫、超市、宾馆、市场的坐标．
（2）分别指出（1）中场所在第几象限？
（3）同学小丽针对这幅图也建立了一个直角坐标系，可是她得到的同一场所的坐标和小明的不一样，是小丽做错了吗？请说明理由．2-1-c-n-j-y
解：（1）体育场的坐标为（﹣2，5），
文化宫的坐标为（﹣1，3），
超市的坐标为（4，﹣1），
宾馆的坐标为（4，4），
市场的坐标为（6，5）；
（2）体育场、文化宫在第二象限，市场、宾馆在第一象限，超市在第四象限；
（3）不是，因为对于同一幅图，直角坐标系的原点、坐标轴方向不同，得到的点的坐标也就不一样．
　
19．某教室中，学生座位的平面图如图所示．
（1）说明王明和张强的位置；
（2）若用（3，2）表示第3排第2列的位置，那么（4，5）表示什么位置？王明和张强的位置可以怎样表示？2·1·c·n·j·y
（3）在（2）的条件下，请说出（3，3）和（4，8）表示哪位同学的位置；
（4）在（2）的条件下，（3，4）和（4，3）表示的位置相同吗？一般地，若a≠b，（a，b）与（b，a）（1≤a≤5，1≤b≤8，a，b为整数）表示的位置相同吗？
解：（1）王明在第2排第2列，张强在第5排第5列；
（2）∵用（3，2）表示第3排第2列的位置，
∴（4，5）表示第4排第5列；
第2排第2列，张强在第5排第5列；
（3）（3，3）表示张逸的位置，（4，8）表示李爽的位置；
（4）（3，4）和（4，3）表示的位置不同，一般地，若a≠b，（a，b）与（b，a）（1≤a≤5，1≤b≤8，a，b为整数）表示的位置不同21·世纪*教育网
　
20．如图的方格中有25个汉字，如四1表示“天”，请沿着以下路径去寻找你的礼物：
（1）一1→三2→二4→四3→五1
一
二
三
四
五
1
我
力
习
天
的
2
会
上
是
学
好
3
帅
就
更
棒
努
4
优
最
行
了
可
5
能
爱
秀
明
哥
（2）五3→二1→二3→一5→三4
（3）四5→四1→一2→三3→五2．
解：（1）一1表示我，三2表示是，二4表示最，四3表示棒，五1表示的，
所以礼物为：我是最棒的；
（2）五3表示努，二1表示力，二3表示就，一5表示能，三4行，
所以礼物为：努力就能行；
（3）四5表示明，四1表示天，一2表示会，三3表示更，五2表示好，
所以礼物为：明天会更好．
　
21．如图1，将射线OX按逆时针方向旋转β角，得到射线OY，如果点P为射线OY上的一点，且OP=a，那么我们规定用（a，β）表示点P在平面内的位置，并记为P（a，β），例如，图2中，如果OM=8，∠XOM=110°，那么点M在平面内的位置，记为M（8，110），根据图形，解答下面的问题：【来源：21·世纪·教育·网】
（1）如图3，如果点N在平面内的位置记为N（6，30），那么ON=　6　；∠XON=　30°　．
（2）如果点A、B在平面内的位置分别记为A（5，30），B（12，120），试求A、B两点之间的距离并画出图．【出处：21教育名师】
解：（1）根据点N在平面内的位置极为N（6，30）可知，ON=6，∠XON=30°．
故答案为：6，30°；
（2）如图所示：∵A（5，30），B（12，120），
∴∠BOX=120°，∠AOX=30°，
∴∠AOB=90°，
∵OA=5，OB=12，
∴在Rt△AOB中，AB==13．