4.2平面直角坐标系同步练习

4.2平面直角坐标系同步练习
　
一．选择题（共10小题）
1．在平面直角坐标系中，若点A（a，﹣b）在第一象限内，则点B（a，b）所在的象限是（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
2．如图为A、B、C三点在坐标平面上的位置图．若A、B、C的x坐标的数字总和为a，y坐标的数字总和为b，则a﹣b之值为何？（　　）【出处：21教育名师】
A．5 B．3 C．﹣3 D．﹣5
3．观察图中正方形四个顶点所标的数字规律，可知，数2016应标在（　　）
A．第504个正方形的左下角 B．第504个正方形的右下角
C．第505个正方形的左上角 D．第505个正方形的右下角
4．若点M（x，y）满足（x+y）2=x2+y2﹣2，则点M所在象限是（　　）
A．第一、三象限 B．第二、四象限 C．第一、二象限 D．不能确定
5．若点A（﹣3，n）在x轴上，则点B（n﹣1，n+1）在（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
6．若点P是第二象限内的点，且点P到x轴的距离是4，到y轴的距离是3，则点P的坐标是（　　）
A．（﹣4，3） B．（4，﹣3） C．（﹣3，4） D．（3，﹣4）
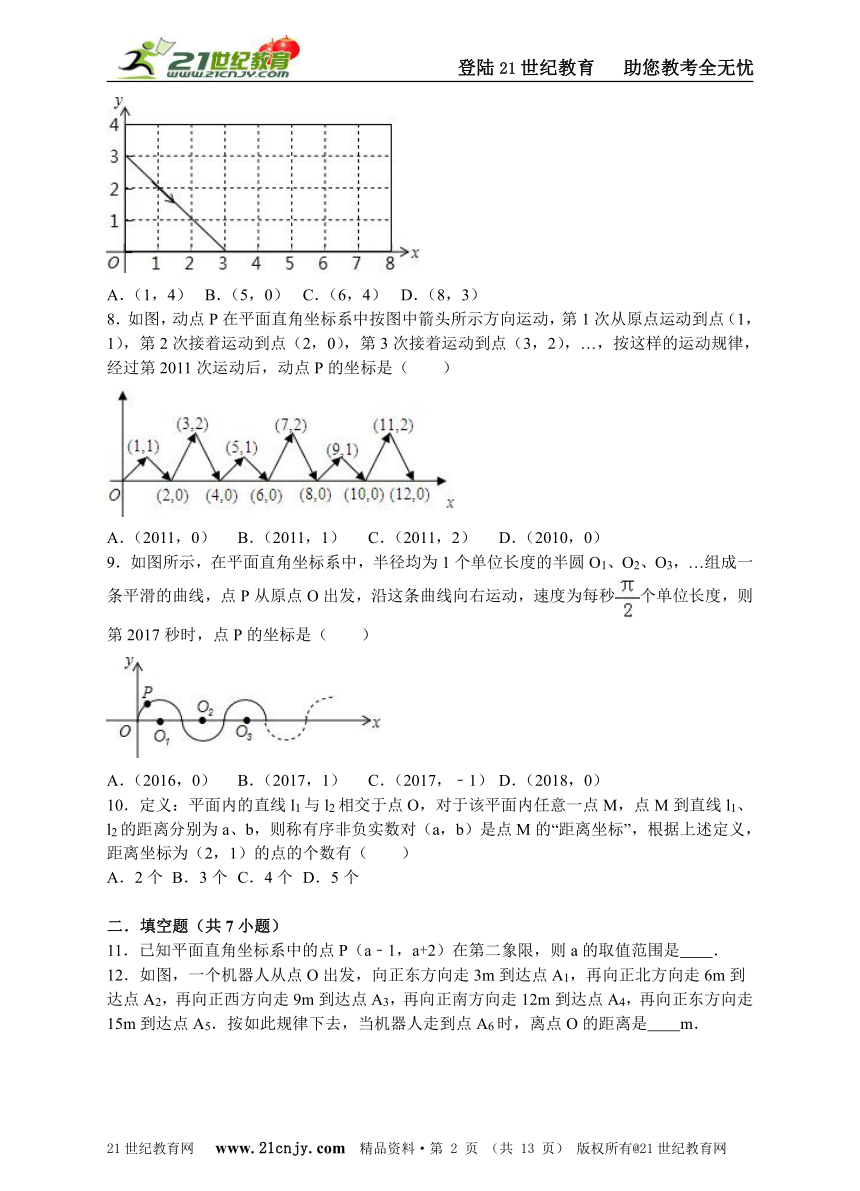
7．如图，动点P从（0，3）出发，沿所示方向运动，每当碰到矩形的边时反弹，反弹时反射角等于入射角，当点P第2014次碰到矩形的边时，点P的坐标为（　　）
A．（1，4） B．（5，0） C．（6，4） D．（8，3）
8．如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过第2011次运动后，动点P的坐标是（　　）21·世纪*教育网
A．（2011，0） B．（2011，1） C．（2011，2） D．（2010，0）
9．如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O1、O2、O3，…组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒个单位长度，则第2017秒时，点P的坐标是（　　）www-2-1-cnjy-com
A．（2016，0） B．（2017，1） C．（2017，﹣1） D．（2018，0）
10．定义：平面内的直线l1与l2相交于点O，对于该平面内任意一点M，点M到直线l1、l2的距离分别为a、b，则称有序非负实数对（a，b）是点M的“距离坐标”，根据上述定义，距离坐标为（2，1）的点的个数有（　　）21*cnjy*com
A．2个 B．3个 C．4个 D．5个
　
二．填空题（共7小题）
11．已知平面直角坐标系中的点P（a﹣1，a+2）在第二象限，则a的取值范围是　　．
12．如图，一个机器人从点O出发，向正东方向走3m到达点A1，再向正北方向走6m到达点A2，再向正西方向走9m到达点A3，再向正南方向走12m到达点A4，再向正东方向走15m到达点A5．按如此规律下去，当机器人走到点A6时，离点O的距离是　　m．
13．在平面直角坐标系中，对于平面内任一点（a，b），若规定以下三种变换：
①f（a，b）=（﹣a，b）．如：f（1，3）=（﹣1，3）；
②g（a，b）=（b，a）．如：g（1，3）=（3，1）；
③h（a，b）=（﹣a，﹣b）．如：h（1，3）=（﹣1，﹣3）．
按照以上变换有：f（g（2，﹣3））=f（﹣3，2）=（3，2），
则f（h（5，﹣3））的值为　　；g（f（5，﹣3））的值为　　．
14．下面四种说法：
①如果一个点的横、纵坐标都为零，则这个点是原点；
②若一个点在x轴上，那它一定不属于任何象限；
③纵轴上的点的横坐标均相等，且都等于零；
④纵坐标相同的点，分布在平行于y轴的某条直线上．
其中你认为正确的有　　．（填序号）
15．如图，在平面直角坐标系中，一动点从原点O出发，沿着箭头所示方向，每次移动1个单位，依次得到点P1（0，1），P2（1，1），P3（1，0），P4（1，﹣1），P5（2，﹣1），P6（2，0），…，则点P60的坐标是　　．21世纪教育网版权所有
16．如图，在直角坐标系中，A（﹣1，2），B（3，﹣2），则△AOB的面积为　　．
17．已知点P的坐标为（2﹣a，3a+6），且点P到两坐标轴的距离相等，则a=　　．
　
三．解答题（共9小题）
18．已知点P（﹣2x，3x+1）是平面直角坐标系中第二象限内的点，且点P到两轴的距离之和为11，求P的坐标．21教育网
19．若x，y为实数，且满足|x﹣3|+=0．
（1）如果实数x，y对应为平面直角坐标系上的点A（x，y），则点A在第几象限？
（2）求（）2015的值？
20．已知：点P（2m+4，m﹣1）．试分别根据下列条件，求出P点的坐标．
（1）点P在y轴上；
（2）点P在x轴上；
（3）点P的纵坐标比横坐标大3；
（4）点P在过A（2，﹣3）点，且与x轴平行的直线上．
21．在平面直角坐标系中，A、B点的位置如图所示，
（1）写出A、B两点的坐标：　　．
（2）若C（﹣3，﹣4）、D（3，﹣3），请在图示坐标系中标出C、D两点．
（3）写出A、B、C、D四点到x轴和y轴的距离：A　　到x轴的距离为　　，到y轴的距离为　　．B　　到x轴的距离为　　，到y轴的距离为　　．21·cn·jy·com
C（﹣3，﹣4）到x轴的距离为　　，到y轴的距离为　　．D（3，﹣3 ）到x轴的距离为　　，到y轴的距离为　　．2-1-c-n-j-y
（4）分析（3）中点的坐标与该点到坐标轴的距离的关系，利用你所发现的结论写出点P（x，y）到x轴的距离为　　，到y轴的距离为　　．【版权所有：21教育】
22．如图，A（﹣1，0），C（1，4），点B在x轴上，且AB=3．
（1）求点B的坐标；
（2）求△ABC的面积；
（3）在y轴上是否存在点P，使以A、B、P三点为顶点的三角形的面积为10？若存在，请直接写出点P的坐标；若不存在，请说明理由．　　21*cnjy*com
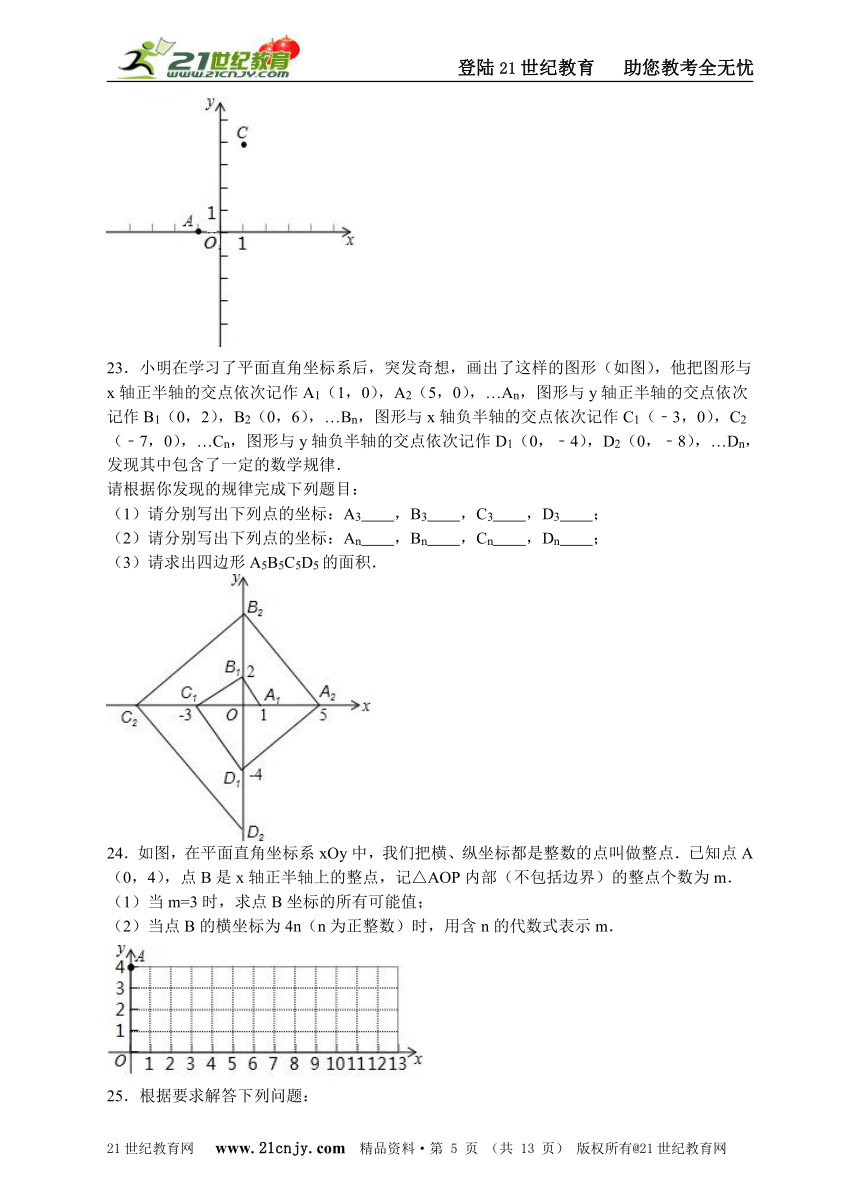
23．小明在学习了平面直角坐标系后，突发奇想，画出了这样的图形（如图），他把图形与x轴正半轴的交点依次记作A1（1，0），A2（5，0），…An，图形与y轴正半轴的交点依次记作B1（0，2），B2（0，6），…Bn，图形与x轴负半轴的交点依次记作C1（﹣3，0），C2（﹣7，0），…Cn，图形与y轴负半轴的交点依次记作D1（0，﹣4），D2（0，﹣8），…Dn，发现其中包含了一定的数学规律．
请根据你发现的规律完成下列题目：
（1）请分别写出下列点的坐标：A3　　，B3　　，C3　　，D3　　；
（2）请分别写出下列点的坐标：An　　，Bn　　，Cn　　，Dn　　；
（3）请求出四边形A5B5C5D5的面积．
24．如图，在平面直角坐标系xOy中，我们把横、纵坐标都是整数的点叫做整点．已知点A（0，4），点B是x轴正半轴上的整点，记△AOP内部（不包括边界）的整点个数为m．
（1）当m=3时，求点B坐标的所有可能值；
（2）当点B的横坐标为4n（n为正整数）时，用含n的代数式表示m．
25．根据要求解答下列问题：
设M（a，b）为平面直角坐标系中的点．
（1）当a＞0，b＜0时，点M位于第几象限？
（2）当ab＞0时，点M位于第几象限？
（3）当a为任意实数，且b＜0时，点M位于何处？
26．根据点的坐标特征回答下列问题．
（1）已知点A（a﹣4，3a+6）在y轴上，则a=　　．
（2）点C（|m|+，+0.01）可能在坐标轴上吗？请说明理由．
（3）已知点B（b2﹣4，1﹣b）在坐标轴上，求b的值．
　

4.2平面直角坐标系同步练习
参考答案与试题解析
　
一．选择题（共10小题）
1． 解：∵点A（a，﹣b）在第一象限内，
∴a＞0，﹣b＞0，
∴b＜0，
∴点B（a，b）所在的象限是第四象限．
故选D．
　
2．解：由图形可知：
a=﹣1+0+5=4，
b=﹣4﹣1+4=﹣1，
a﹣b=4+1=5．
故选：A．
　
3．解：∵2016÷4=504，
又∵由题目中给出的几个正方形观察可知，每个正方形对应四个数，而第一个最小的数是0，0在右下角，然后按逆时针由小变大，
∴第504个正方形中最大的数是2015，
∴数2016在第505个正方形的右下角，
故选D．
　
4． 解：∵（x+y）2=x2+2xy+y2，
∴2xy=﹣2，
xy=﹣1，
∴x、y异号，
∴点M（x，y）在第二、四象限．
故选B．
　
5．解：∵点A（﹣3，n）在x轴上，
∴n=0，
∴点B（﹣1，1），
∴点B在第二象限．
故选B．
　
6．解：∵点P在第二象限，
∴P点的横坐标为负，纵坐标为正，
∵到x轴的距离是4，
∴纵坐标为：4，
∵到y轴的距离是3，
∴横坐标为：﹣3，
∴P（﹣3，4），
故选：C．
　
7．解：如图，经过6次反弹后动点回到出发点（0，3），
∵2014÷6=335…4，
∴当点P第2014次碰到矩形的边时为第336个循环组的第4次反弹，
点P的坐标为（5，0）．
故选；B．
　
8．解：∵第1次运动到点（1，1），第2次运动到点（2，0），第3次接着运动到点（3，2），第4次运动到点（4，0），第5次运动到点（5，1）…，21cnjy.com
∴运动后点的横坐标等于运动的次数，
第2011次运动后点P的横坐标为2011，
纵坐标以1、0、2、0每4次为一个循环组循环，
∵2011÷4=502…3，
∴第2011次运动后动点P的纵坐标是第503个循环组的第3次运动，与第3次运动的点的纵坐标相同，为2，www.21-cn-jy.com
∴点P（2011，2）．
故选C．
　
9．解：以时间为点P的下标．
观察，发现规律：P0（0，0），P1（1，1），P2（2，0），P3（3，﹣1），P4（4，0），P5（5，1），…，2·1·c·n·j·y
∴P4n（n，0），P4n+1（4n+1，1），P4n+2（4n+2，0），P4n+3（4n+3，﹣1）．
∵2017=504×4+1，
∴第2017秒时，点P的坐标为（2017，1）．
故选B
　
10．解：如图1，，
到l1的距离为2的点是两条平行直线l3、l4，到l2的距离为1的点也是两条平行直线l5、l6，
∵两组直线的交点一共有4个：A、B、C、D，
∴距离坐标为（2，1）的点的个数有4个．
故选：C．
　
二．填空题（共7小题）
11．解：∵平面直角坐标系中的点P（a﹣1，a+2）在第二象限，
∴
解得﹣2＜a＜1，
即a的取值范围是：﹣2＜a＜1．
故答案为：﹣2＜a＜1．
　
12．解：根据题意可知当机器人走到A6点时，
A5A6=18米，
点A6的坐标是（6+3=9，18﹣6=12），
即（9，12）．
所以，当机器人走到点A6时，
离东西方向所在的直线的距离是12m．
故答案为：12．
　
13．解：f（h（5，﹣3））=f（﹣5，3）=（5，3），
g（f（5，﹣3））=g（﹣5，﹣3）=（﹣3，﹣5）．
故答案为：（5，3）、（﹣3，﹣5）．
　
14．解：①如果一个点的横、纵坐标都为零，则这个点是原点，正确；
②若一个点在x轴上，那它一定不属于任何象限，正确；
③纵轴上的点的横坐标均相等，且都等于零，正确；
④纵坐标相同的点，分布在平行于y轴的某条直线上，错误．
故答案为：①②③．
　
15．解：∵P3（1，0），P6（2，0），P9（3，0），…，
∴P3n（n，0）
当n=20时，P60（20，0），
故答案为：（20，0）．
　
16．解：△AOB的面积为：×4×4﹣×1×2﹣2﹣×2×3=2．
故答案为：2．
　
17．解：根据题意得|2﹣a|=|3a+6|，
所以2﹣a=3a+6或2﹣a=﹣（3a+6），
解得a=﹣1或a=﹣4．
故答案为﹣1或﹣4．
　
三．解答题（共9小题）
18．解：∵点P（﹣2x，3x+1）在第二象限，且到两轴的距离之和为11，
∴2x+3x+1=11，
解得x=2，
所以，﹣2x=﹣2×2=﹣4，
3x+1=3×2+1=7，
所以，点P的坐标为（﹣4，7）．
　
19．解：（1）∵|x+3|≥0，≥0，且|x﹣3|+=0，
∴x﹣3=0，y+3=0，
∴x=3，y=﹣3，
∴A（3，﹣3），
∴点A在第四象限．
（2）由（1）得：x=3，y=﹣3，
∴=﹣1，
∴（）2015=﹣1．
　
20．解：（1）令2m+4=0，解得m=﹣2，所以P点的坐标为（0，﹣3）；
（2）令m﹣1=0，解得m=1，所以P点的坐标为（6，0）；
（3）令m﹣1=（2m+4）+3，解得m=﹣8，所以P点的坐标为（﹣12，﹣9）；
（4）令m﹣1=﹣3，解得m=﹣2．所以P点的坐标为（0，﹣3）．
　
21．解：（1）如图可得A（1，2），B（﹣3，2）；
（2）如图；
（3）到x轴的距离等于该点纵坐标的绝对值；到y轴的距离等于该点横坐标的绝对值，
（1，2）；2；1；（﹣3，2）；2；3；4；3；3；3；
（4）|y|，|x|；
故答案为A（1，2），B（﹣3，2）； 如图；（1，2），2，1，（﹣3，2），2，3，4，3，3，3；【来源：21·世纪·教育·网】
|y|，|x|．
　
22．解：（1）点B在点A的右边时，﹣1+3=2，
点B在点A的左边时，﹣1﹣3=﹣4，
所以，B的坐标为（2，0）或（﹣4，0）；
（2）△ABC的面积=×3×4=6；
（3）设点P到x轴的距离为h，
则×3h=10，
解得h=，
点P在y轴正半轴时，P（0，），
点P在y轴负半轴时，P（0，﹣），
综上所述，点P的坐标为（0，）或（0，﹣）．
　
23．解：（1）A3（9，0），B3（0，10），C3（﹣11，0），D3（0，﹣12）．
（2）An（4n﹣3，0），Bn（0，4n﹣2），Cn（﹣4n+1，0），Dn（0，﹣4n）．
（3）∵A5（17，0），B5（0，18），C5（﹣19，0），D5（0，﹣20）．
∴四边形A5B5C5D5的面积=+++=×17×18+×18×19+×19×20+×20×17=684．【来源：21cnj*y.co*m】
故答案为：A3（9，0），B3（0，10），C3（﹣11，0），D3（0，﹣12）．
An（4n﹣3，0），Bn（0，4n﹣2），Cn（﹣4n+1，0），Dn（0，﹣4n）．
　
24．解：（1）当B点的横坐标为3或者4时，即B（3，0）或（4，0）如下图所示，只有3个整点，
坐标分别为（1，1），（1，2），（2，1）；
（2）当n=1时，即B点的横坐标为4，如上图，此时有3个整点；
当n=2时，即B点的横坐标为8，如图1，此时有9个整点；
当n=3时，即B点的横坐标为12，如图2，此时有15个整点；
根据上面的规律，即可得出3，9，15…，
∴整数点m=6n﹣3，
理由如下：当点B的横坐标为4n（n为正整数）时，
∵以OB为长OA为宽的矩形内（不包括边界）的整点个数为（4n﹣1）×3=12n﹣3，对角线AB上的整点个数总为3，21教育名师原创作品
∴△AOB内部（不包括边界）的整点个数m=（12n﹣3﹣3）÷2=6n﹣3．
　
25．解：∵M（a，b）为平面直角坐标系中的点．
（1）当a＞0，b＜0时，点M位于第四象限；
（2）当ab＞0时，即a，b同号，故点M位于第一、三象限；
（3）当a为任意实数，且b＜0时，点M位于第三、四象限和纵轴的负半轴．
　
26．根据点的坐标特征回答下列问题．
（1）已知点A（a﹣4，3a+6）在y轴上，则a=　4　．
（2）点C（|m|+，+0.01）可能在坐标轴上吗？请说明理由．
（3）已知点B（b2﹣4，1﹣b）在坐标轴上，求b的值．
解：（1）∵点A（a﹣4，3a+6）在y轴上，
∴a﹣4=0．
解得：a=4．
故答案为：4．
（2）∵|m|≥0，≥0，
∴|m+＞0，．
∴点C在第一象限．
∴点B不可能在坐标轴上．
（3）当点B在x坐标轴上时，1﹣b=0，
∴b=1．
当点B在x坐标轴y上时，b2﹣4=0，
解得b=±2．