九年级数学(浙教版)上册复习课件第1章二次函数 (共22张PPT)
文档属性
| 名称 | 九年级数学(浙教版)上册复习课件第1章二次函数 (共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-11 15:38:30 | ||
图片预览





文档简介
课件22张PPT。第1章 二次函数1.由二次函数y=2(x-3)2+1,可知( )
A.其图象的开口向下 B.其图象的对称轴为直线x=-3
C.其最小值为1 D.当x<3时,y随x的增大而增大2.下列函数中,当x>0时y值随x值的增大而减小的是( )A.开口向下 B.对称轴是直线x=-3
C.顶点坐标是(3,2) D.顶点是抛物线的最高点CDB 4.二次函数的图象经过(0,3),(-2,-5),(1,4)三点,则它的表达式为( )
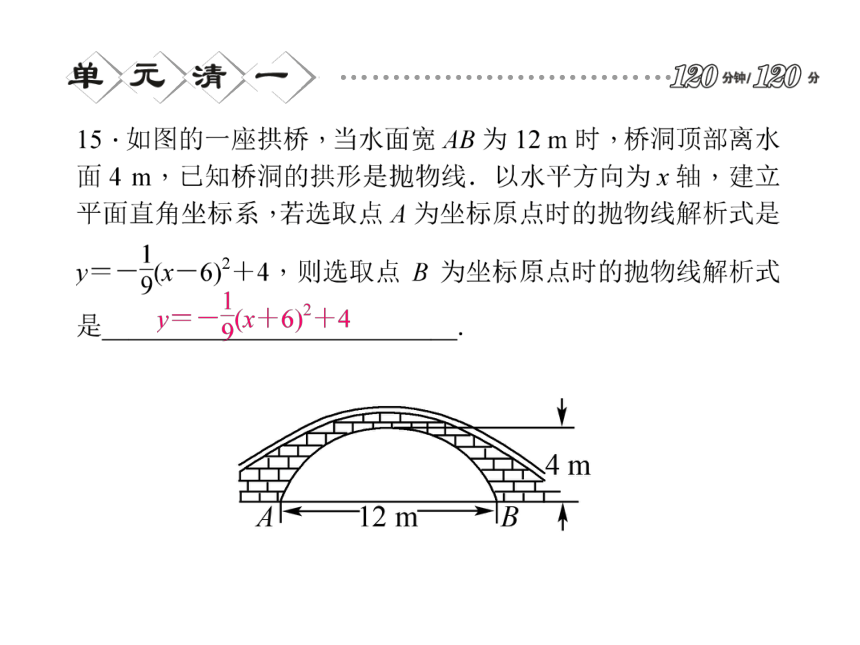
A.y=-x2+2x+3 B.y=x2-x+3
C.y=-x2-2x+3 D.y=x2-2x+35.已知抛物线y=ax2+bx+c(a<0)过A(-2,0),O(0,0),B(-3,y1),C(3,y2)四点,则y1与y2的大小关系是( )
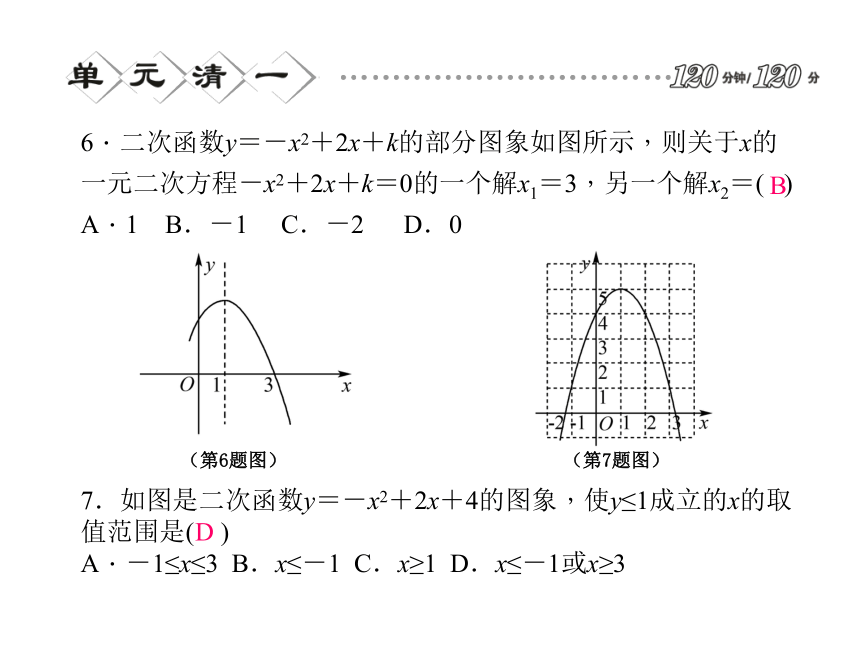
A.y1>y2 B.y1=y2 C.y1<y2 D.不能确定AA6.二次函数y=-x2+2x+k的部分图象如图所示,则关于x的一元二次方程-x2+2x+k=0的一个解x1=3,另一个解x2=( )
A.1 B.-1 C.-2 D.07.如图是二次函数y=-x2+2x+4的图象,使y≤1成立的x的取值范围是( )
A.-1≤x≤3 B.x≤-1 C.x≥1 D.x≤-1或x≥3(第6题图) (第7题图) BD8.二次函数y=-x2+1的图象与x轴交于A,B两点,与y轴相交于点C.下列说法中,错误的是( )
A.△ABC是等腰三角形 B.点C的坐标是(0,1)
C.AB的长为2 D.y随x的增大而减小9.已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③a-2b+4c<0;④8a+c>0.其中正确的有( )
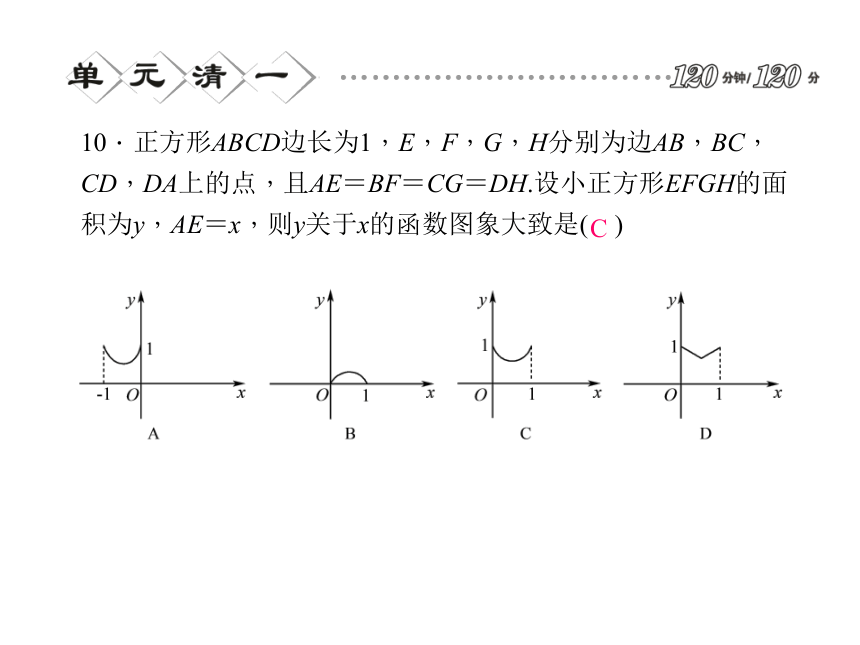
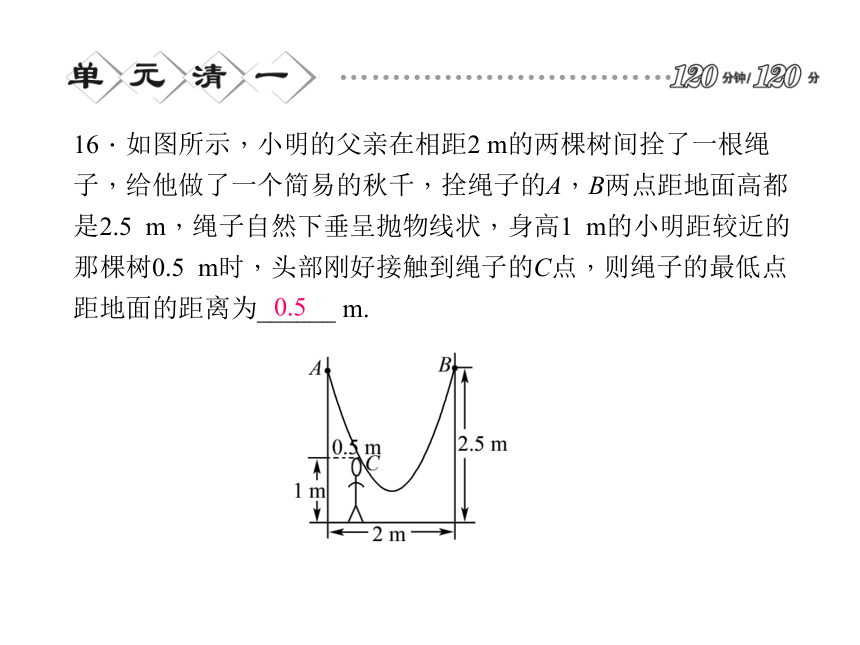
A.3个 B.2个 C.1个 D.0个DB10.正方形ABCD边长为1,E,F,G,H分别为边AB,BC,CD,DA上的点,且AE=BF=CG=DH.设小正方形EFGH的面积为y,AE=x,则y关于x的函数图象大致是( )C11.二次函数y=2(x-2)(x+3)的图象的顶点坐标是_________,对称轴是___________,开口方向_______.12.已知二次函数y=x2+bx+3的对称轴为x=2,则b=______.13.将抛物线y=2(x+1)2-3向右平移1个单位,再向上平移3个单位,所得抛物线的表达式为________.14.二次函数y=x2+bx+c的图象经过A(-1,0),B(3,0)两点,则其顶点坐标是_____________.向上-4y=2x2(1,-4)16.如图所示,小明的父亲在相距2 m的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的A,B两点距地面高都是2.5 m,绳子自然下垂呈抛物线状,身高1 m的小明距较近的那棵树0.5 m时,头部刚好接触到绳子的C点,则绳子的最低点距地面的距离为______ m.0.517.(10分)已知二次函数y=x2-2x-3.
(1)求图象的开口方向、对称轴、顶点坐标;
(2)求图象与x轴的交点坐标,与y轴的交点坐标;
(3)当x为何值时,y随x的增大而增大?解:(1)∵a=1>0,∴图象开口向上.∵y=x2-2x-3=(x-1)2-4,∴图象的对称轴是x=1,顶点坐标是(1,-4)
(2)令x=0,得y=-3,∴图象与y轴的交点坐标是(0,-3).令y=0,得x2-2x-3=0,解方程得x=3或x=-1,∴图象与x轴的交点坐标是(3,0),(-1,0)
(3)∵图象的对称轴为x=1,图象开口向上,∴当x≥1时,y随x的增大而增大18.(6分)如图,已知二次函数y=-x2+bx+3的图象与x轴的一个交点为A(4,0),与y轴交于点B.求此二次函数的解析式和点B的坐标.19.(6分)已知二次函数的图象以A(-1,4)为顶点,且过点B(2,-5).
(1)求该函数的解析式;
(2)求该函数图象与坐标轴的交点坐标.解:(1)由A(-1,4)为抛物线顶点,设抛物线解析式为y=a(x+1)2+4,将点B(2,-5)代入,得9a+4=-5,解得a=-1,∴y=-(x+1)2+4
(2)∵y=-(x+1)2+4=-x2-2x+3=-(x-1)(x+3),令y=0,则x1=1,x2=-3;令x=0,则y=3,∴抛物线与y轴的交点坐标为(0,3),与x轴的交点坐标为(1,0),(-3,0).20.(6分)如图所示,一位运动员在离篮筐下水平距离4米处起跳投篮,球运行的路线是抛物线,当球运行的水平距离是2.5米时,球达到最大高度3.5米.已知篮筐中心到地面的距离为3.05米,问球出手时离地面多少米才能投中篮筐.解:由题意可知,点C的坐标为(0,3.5),点B的坐标为(1.5,3.05),设抛物线的解析式为y=ax2+3.5,代入B点坐标得a=-0.2,因此抛物线的解析式为y=-0.2x2+3.5,把x=-2.5代入抛物线的解析式得y=2.25.
答:球出手时离地面2.25米才能投中篮筐.21.(8分)如图所示,在一块等腰直角△ABC铁皮上截一块矩形EFGD,边FG在AB上,顶点E,D分别在边CA,CB上,底边AB长20厘米.设EF的长为x厘米,矩形EFGD的面积为y平方厘米,试写出y关于x的函数关系式及自变量的取值范围,并求当EF的长为4厘米时,所截得的矩形的面积.解:∵△ABC是等腰直角三角形,四边形EFGD是矩形,∴△AFE和△DGB都是等腰直角三角形,
∴AF=EF=x,GB=DG=x,FG=AB-AF-GB=20-2x,
矩形EFGD的面积y=x(20-2x)=-2x2+20x,
由0<20-2x<20,解得0<x<10,
∴y关于x的函数关系式是y=-2x2+20x(0<x<10),
当x=4时,y=-2×42+20×4=48,
即当EF的长为4厘米时,所截得的矩形的面积为48平方厘米22.(10分)实验数据显示,一般成人喝半斤白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数y= (k>0)刻画(如图所示).
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当x=5时,y=45,求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.23.(10分)如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点.
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.(3)画图略.x的取值范围为-1<x<4 24.(10分)如图,一次函数y=- x+2分别交y轴,x轴于A,B两点,抛物线y=-x2+bx+c过A,B两点.
(1)求这个抛物线的解析式;
(2)作垂直于x轴的直线x=t,在第一象限交直线AB于点M,交这个抛物线于点N,求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下(即MN取最大值时),以A,M,N,D为顶点作平行四边形,求第四个顶点D的坐标.
A.其图象的开口向下 B.其图象的对称轴为直线x=-3
C.其最小值为1 D.当x<3时,y随x的增大而增大2.下列函数中,当x>0时y值随x值的增大而减小的是( )A.开口向下 B.对称轴是直线x=-3
C.顶点坐标是(3,2) D.顶点是抛物线的最高点CDB 4.二次函数的图象经过(0,3),(-2,-5),(1,4)三点,则它的表达式为( )
A.y=-x2+2x+3 B.y=x2-x+3
C.y=-x2-2x+3 D.y=x2-2x+35.已知抛物线y=ax2+bx+c(a<0)过A(-2,0),O(0,0),B(-3,y1),C(3,y2)四点,则y1与y2的大小关系是( )
A.y1>y2 B.y1=y2 C.y1<y2 D.不能确定AA6.二次函数y=-x2+2x+k的部分图象如图所示,则关于x的一元二次方程-x2+2x+k=0的一个解x1=3,另一个解x2=( )
A.1 B.-1 C.-2 D.07.如图是二次函数y=-x2+2x+4的图象,使y≤1成立的x的取值范围是( )
A.-1≤x≤3 B.x≤-1 C.x≥1 D.x≤-1或x≥3(第6题图) (第7题图) BD8.二次函数y=-x2+1的图象与x轴交于A,B两点,与y轴相交于点C.下列说法中,错误的是( )
A.△ABC是等腰三角形 B.点C的坐标是(0,1)
C.AB的长为2 D.y随x的增大而减小9.已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③a-2b+4c<0;④8a+c>0.其中正确的有( )
A.3个 B.2个 C.1个 D.0个DB10.正方形ABCD边长为1,E,F,G,H分别为边AB,BC,CD,DA上的点,且AE=BF=CG=DH.设小正方形EFGH的面积为y,AE=x,则y关于x的函数图象大致是( )C11.二次函数y=2(x-2)(x+3)的图象的顶点坐标是_________,对称轴是___________,开口方向_______.12.已知二次函数y=x2+bx+3的对称轴为x=2,则b=______.13.将抛物线y=2(x+1)2-3向右平移1个单位,再向上平移3个单位,所得抛物线的表达式为________.14.二次函数y=x2+bx+c的图象经过A(-1,0),B(3,0)两点,则其顶点坐标是_____________.向上-4y=2x2(1,-4)16.如图所示,小明的父亲在相距2 m的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的A,B两点距地面高都是2.5 m,绳子自然下垂呈抛物线状,身高1 m的小明距较近的那棵树0.5 m时,头部刚好接触到绳子的C点,则绳子的最低点距地面的距离为______ m.0.517.(10分)已知二次函数y=x2-2x-3.
(1)求图象的开口方向、对称轴、顶点坐标;
(2)求图象与x轴的交点坐标,与y轴的交点坐标;
(3)当x为何值时,y随x的增大而增大?解:(1)∵a=1>0,∴图象开口向上.∵y=x2-2x-3=(x-1)2-4,∴图象的对称轴是x=1,顶点坐标是(1,-4)
(2)令x=0,得y=-3,∴图象与y轴的交点坐标是(0,-3).令y=0,得x2-2x-3=0,解方程得x=3或x=-1,∴图象与x轴的交点坐标是(3,0),(-1,0)
(3)∵图象的对称轴为x=1,图象开口向上,∴当x≥1时,y随x的增大而增大18.(6分)如图,已知二次函数y=-x2+bx+3的图象与x轴的一个交点为A(4,0),与y轴交于点B.求此二次函数的解析式和点B的坐标.19.(6分)已知二次函数的图象以A(-1,4)为顶点,且过点B(2,-5).
(1)求该函数的解析式;
(2)求该函数图象与坐标轴的交点坐标.解:(1)由A(-1,4)为抛物线顶点,设抛物线解析式为y=a(x+1)2+4,将点B(2,-5)代入,得9a+4=-5,解得a=-1,∴y=-(x+1)2+4
(2)∵y=-(x+1)2+4=-x2-2x+3=-(x-1)(x+3),令y=0,则x1=1,x2=-3;令x=0,则y=3,∴抛物线与y轴的交点坐标为(0,3),与x轴的交点坐标为(1,0),(-3,0).20.(6分)如图所示,一位运动员在离篮筐下水平距离4米处起跳投篮,球运行的路线是抛物线,当球运行的水平距离是2.5米时,球达到最大高度3.5米.已知篮筐中心到地面的距离为3.05米,问球出手时离地面多少米才能投中篮筐.解:由题意可知,点C的坐标为(0,3.5),点B的坐标为(1.5,3.05),设抛物线的解析式为y=ax2+3.5,代入B点坐标得a=-0.2,因此抛物线的解析式为y=-0.2x2+3.5,把x=-2.5代入抛物线的解析式得y=2.25.
答:球出手时离地面2.25米才能投中篮筐.21.(8分)如图所示,在一块等腰直角△ABC铁皮上截一块矩形EFGD,边FG在AB上,顶点E,D分别在边CA,CB上,底边AB长20厘米.设EF的长为x厘米,矩形EFGD的面积为y平方厘米,试写出y关于x的函数关系式及自变量的取值范围,并求当EF的长为4厘米时,所截得的矩形的面积.解:∵△ABC是等腰直角三角形,四边形EFGD是矩形,∴△AFE和△DGB都是等腰直角三角形,
∴AF=EF=x,GB=DG=x,FG=AB-AF-GB=20-2x,
矩形EFGD的面积y=x(20-2x)=-2x2+20x,
由0<20-2x<20,解得0<x<10,
∴y关于x的函数关系式是y=-2x2+20x(0<x<10),
当x=4时,y=-2×42+20×4=48,
即当EF的长为4厘米时,所截得的矩形的面积为48平方厘米22.(10分)实验数据显示,一般成人喝半斤白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数y= (k>0)刻画(如图所示).
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当x=5时,y=45,求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.23.(10分)如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点.
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.(3)画图略.x的取值范围为-1<x<4 24.(10分)如图,一次函数y=- x+2分别交y轴,x轴于A,B两点,抛物线y=-x2+bx+c过A,B两点.
(1)求这个抛物线的解析式;
(2)作垂直于x轴的直线x=t,在第一象限交直线AB于点M,交这个抛物线于点N,求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下(即MN取最大值时),以A,M,N,D为顶点作平行四边形,求第四个顶点D的坐标.
同课章节目录
