九年级数学(浙教版)上册复习课件_第4章相似三角形 (共19张PPT)
文档属性
| 名称 | 九年级数学(浙教版)上册复习课件_第4章相似三角形 (共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-11 15:43:29 | ||
图片预览



文档简介
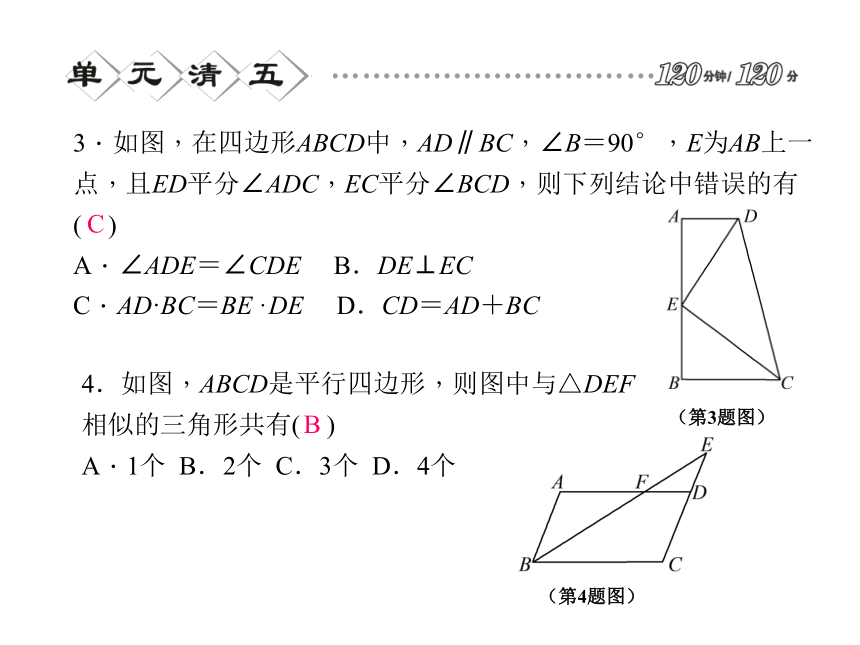
课件19张PPT。第4章 相似三角形A C 3.如图,在四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,且ED平分∠ADC,EC平分∠BCD,则下列结论中错误的有( )
A.∠ADE=∠CDE B.DE⊥EC
C.AD·BC=BE·DE D.CD=AD+BC C4.如图,ABCD是平行四边形,则图中与△DEF相似的三角形共有( )
A.1个 B.2个 C.3个 D.4个B(第3题图) (第4题图) B 6.两个相似多边形的面积比是9∶16,其中较小多边形的周长为36 cm,则较大多边形的周长为( )
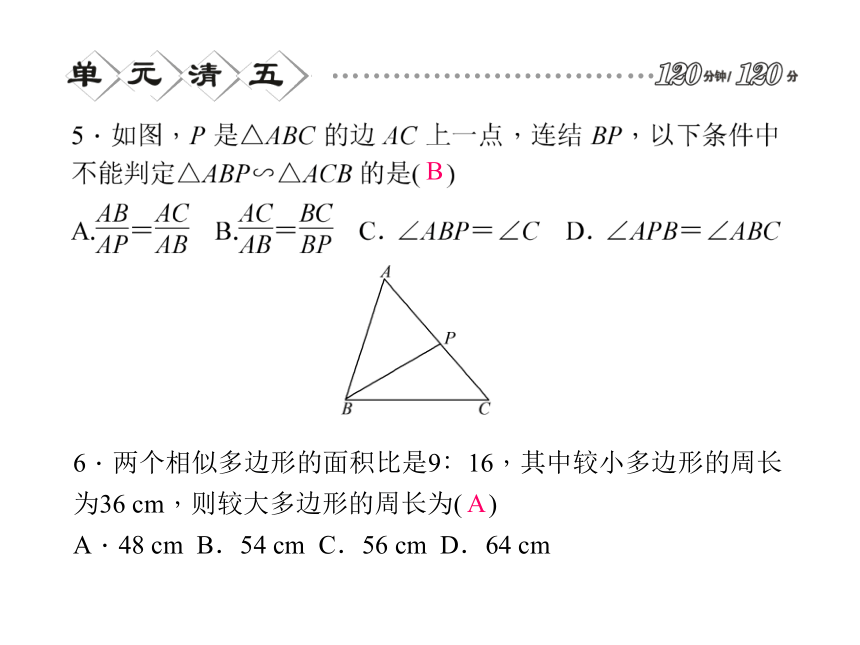
A.48 cm B.54 cm C.56 cm D.64 cmA7.如图,在梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=2,DC=3,则△ABC与△DCA的面积比为( )
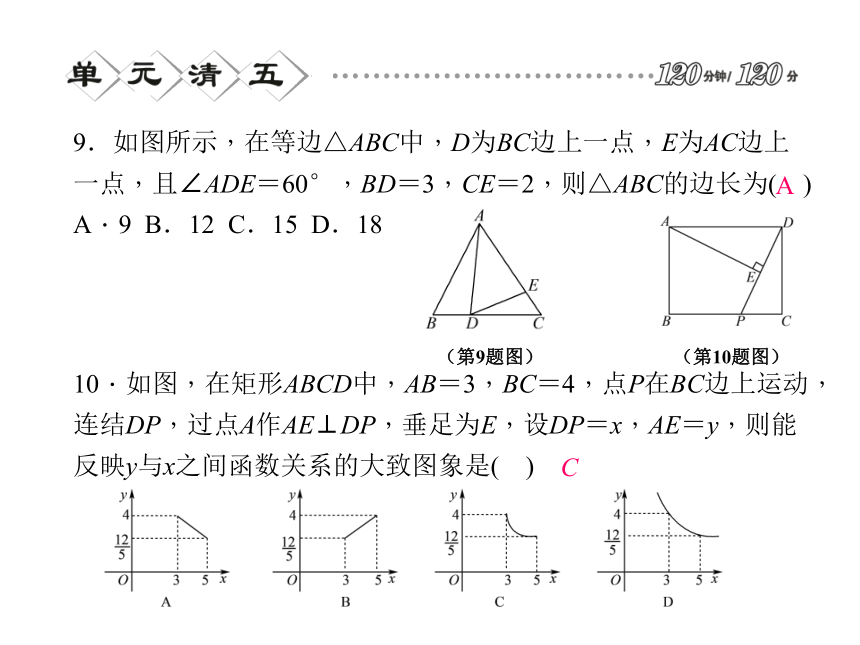
A.2∶3 B.2∶5 C.4∶9 D.C8.如图,A,B,C,D是⊙O上的四个点,AB=AC,AD交BC于点E,AE=3,ED=4,则AB的长为( )C9.如图所示,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的边长为( )
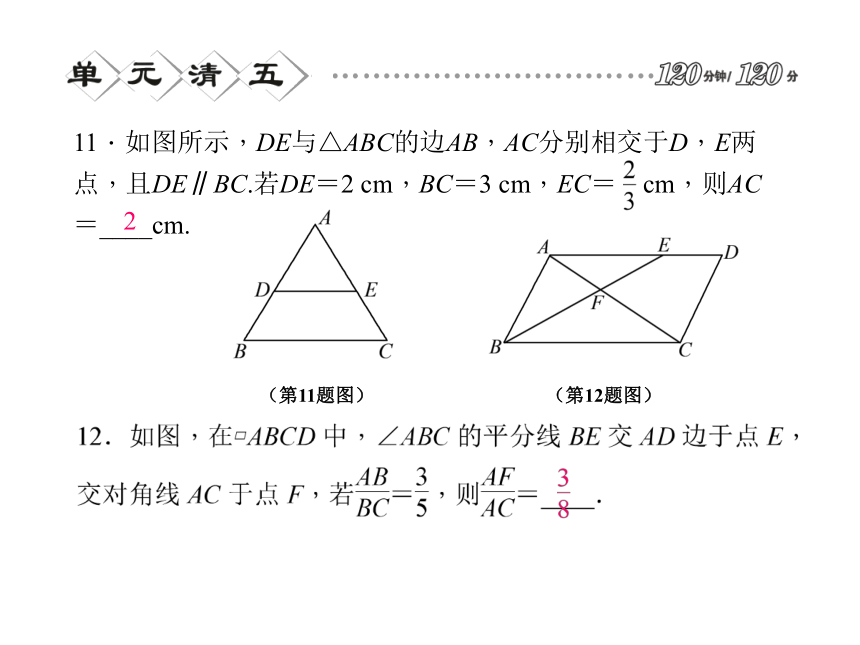
A.9 B.12 C.15 D.1810.如图,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动,连结DP,过点A作AE⊥DP,垂足为E,设DP=x,AE=y,则能反映y与x之间函数关系的大致图象是( )(第10题图) (第9题图) AC11.如图所示,DE与△ABC的边AB,AC分别相交于D,E两点,且DE∥BC.若DE=2 cm,BC=3 cm,EC= cm,则AC=____cm.2(第11题图) (第12题图) 13.如图,小明用长为3 m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12 m,则旗杆AB的高为____m.(第13题图) (第14题图) 14.如图,△ABC中,D,E分别为AC,BC边上的点,AB∥DE,CF为AB边上的中线,若AD=5,CD=3,DE=4,则BF的长为____.915.将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF,已知AB=AC=3,BC=4,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是______________.①②③ (第15题图)(第16题图)17.(6分)如图,BD与CE相交于点A,已知AB=6,AC=4,AD=3,且△ABC∽△ADE,求AE的长.19.(8分)如图,O为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,求y与x的函数关系式.20.(8分)如图,已知△ABC中,D是AC边上一点,∠A=36°,∠C=72°,∠ADB=108°.求证:
(1)AD=BD=BC;
(2)点D是线段AC的黄金分割点.证明:(1)∵∠A=36°,∠C=72°,∴∠ABC=72°.∵∠A=36°,∠ADB=108°,∴∠ABD=36°,∴∠DBC=∠ABC-∠ABD=36°,∴∠BDC=180°-∠DBC-∠C=72°,∴△ADB、△BDC是等腰三角形,∴AD=BD=BC (2)∵∠DBC=∠A=36°,∠C=∠C,∴△ABC∽△BDC,∴BC∶DC=AC∶BC.∵BC=AD,∴AD∶DC=AC∶AD,
∴点D是线段AC的黄金分割点21.(8分)某一天,小明和小亮来到一河边,想用遮阳帽和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,先在河岸边选择了一点B(点B与河对岸岸边上的一棵树的底部点D所确定的直线垂直于河岸).
①小明在B点面向树的方向站好,调整帽檐,使视线通过帽檐正好落在树的底部点D处,如图所示,这时小亮测得小明眼睛距地面AB=1.7米;
②小明站在原地转动180°后蹲下,并保持原来的观察姿态(除身体重心下移外,其他姿态均不变),这时视线通过帽檐落在了DB延长线上的点E处,此时小亮测得BE=9.6米,小明的眼睛距地面的距离CB=1.2米.
根据以上测量过程及测量数据,请你求出河宽BD是多少米?22.(8分)如图所示,在△ABC中,D是BC边上一点,E是AC边上一点,且满足AD=AB,∠ADE=∠C.求证:
(1)∠AED=∠ADC,∠DEC=∠B;
(2)AB2=AE·AC.证明:(1)在△ADE和△ACD中,∵∠ADE=∠C,∠DAE=∠DAE,∴△ADE∽△ACD,∴∠AED=∠ADC.∵∠AED+∠DEC=180°,∠ADB+∠ADC=180°,∴∠DEC=∠ADB.又∵AB=AD,∴∠ADB=∠B,∴∠DEC=∠B 23.(10分)在圆内接四边形ABCD中,CD为△BCA外角的平分线,F为弧AD上一点,BC=AF,延长DF与BA的延长线交于点E.求证:
(1)△ABD为等腰三角形;
(2)AC·AF=DF·FE.证明:(1)由“圆的内接四边形的外角等于它的内对角”知∠MCD=∠BAD.又∠DCA=∠DBA,∠MCD=∠DCA,∴∠DBA=∠DAB,∴△ABD为等腰三角形 24.(12分)如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D.求证:
(1)D是BC的中点;
(2)△BEC∽△ADC;
(3)BC2=2AB·CE.证明:(1)∵AB是⊙O的直径,
∴∠ADB=90°,即AD是底边BC上的高,
又∵AB=AC,
∴△ABC是等腰三角形,∴D是BC的中点; (2)∵∠CBE与∠CAD是 所对的圆周角,∴∠CBE=∠CAD,又∵∠BCE=∠ACD,∴△BEC∽△ADC;
A.∠ADE=∠CDE B.DE⊥EC
C.AD·BC=BE·DE D.CD=AD+BC C4.如图,ABCD是平行四边形,则图中与△DEF相似的三角形共有( )
A.1个 B.2个 C.3个 D.4个B(第3题图) (第4题图) B 6.两个相似多边形的面积比是9∶16,其中较小多边形的周长为36 cm,则较大多边形的周长为( )
A.48 cm B.54 cm C.56 cm D.64 cmA7.如图,在梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=2,DC=3,则△ABC与△DCA的面积比为( )
A.2∶3 B.2∶5 C.4∶9 D.C8.如图,A,B,C,D是⊙O上的四个点,AB=AC,AD交BC于点E,AE=3,ED=4,则AB的长为( )C9.如图所示,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的边长为( )
A.9 B.12 C.15 D.1810.如图,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动,连结DP,过点A作AE⊥DP,垂足为E,设DP=x,AE=y,则能反映y与x之间函数关系的大致图象是( )(第10题图) (第9题图) AC11.如图所示,DE与△ABC的边AB,AC分别相交于D,E两点,且DE∥BC.若DE=2 cm,BC=3 cm,EC= cm,则AC=____cm.2(第11题图) (第12题图) 13.如图,小明用长为3 m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12 m,则旗杆AB的高为____m.(第13题图) (第14题图) 14.如图,△ABC中,D,E分别为AC,BC边上的点,AB∥DE,CF为AB边上的中线,若AD=5,CD=3,DE=4,则BF的长为____.915.将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF,已知AB=AC=3,BC=4,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是______________.①②③ (第15题图)(第16题图)17.(6分)如图,BD与CE相交于点A,已知AB=6,AC=4,AD=3,且△ABC∽△ADE,求AE的长.19.(8分)如图,O为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,求y与x的函数关系式.20.(8分)如图,已知△ABC中,D是AC边上一点,∠A=36°,∠C=72°,∠ADB=108°.求证:
(1)AD=BD=BC;
(2)点D是线段AC的黄金分割点.证明:(1)∵∠A=36°,∠C=72°,∴∠ABC=72°.∵∠A=36°,∠ADB=108°,∴∠ABD=36°,∴∠DBC=∠ABC-∠ABD=36°,∴∠BDC=180°-∠DBC-∠C=72°,∴△ADB、△BDC是等腰三角形,∴AD=BD=BC (2)∵∠DBC=∠A=36°,∠C=∠C,∴△ABC∽△BDC,∴BC∶DC=AC∶BC.∵BC=AD,∴AD∶DC=AC∶AD,
∴点D是线段AC的黄金分割点21.(8分)某一天,小明和小亮来到一河边,想用遮阳帽和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,先在河岸边选择了一点B(点B与河对岸岸边上的一棵树的底部点D所确定的直线垂直于河岸).
①小明在B点面向树的方向站好,调整帽檐,使视线通过帽檐正好落在树的底部点D处,如图所示,这时小亮测得小明眼睛距地面AB=1.7米;
②小明站在原地转动180°后蹲下,并保持原来的观察姿态(除身体重心下移外,其他姿态均不变),这时视线通过帽檐落在了DB延长线上的点E处,此时小亮测得BE=9.6米,小明的眼睛距地面的距离CB=1.2米.
根据以上测量过程及测量数据,请你求出河宽BD是多少米?22.(8分)如图所示,在△ABC中,D是BC边上一点,E是AC边上一点,且满足AD=AB,∠ADE=∠C.求证:
(1)∠AED=∠ADC,∠DEC=∠B;
(2)AB2=AE·AC.证明:(1)在△ADE和△ACD中,∵∠ADE=∠C,∠DAE=∠DAE,∴△ADE∽△ACD,∴∠AED=∠ADC.∵∠AED+∠DEC=180°,∠ADB+∠ADC=180°,∴∠DEC=∠ADB.又∵AB=AD,∴∠ADB=∠B,∴∠DEC=∠B 23.(10分)在圆内接四边形ABCD中,CD为△BCA外角的平分线,F为弧AD上一点,BC=AF,延长DF与BA的延长线交于点E.求证:
(1)△ABD为等腰三角形;
(2)AC·AF=DF·FE.证明:(1)由“圆的内接四边形的外角等于它的内对角”知∠MCD=∠BAD.又∠DCA=∠DBA,∠MCD=∠DCA,∴∠DBA=∠DAB,∴△ABD为等腰三角形 24.(12分)如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D.求证:
(1)D是BC的中点;
(2)△BEC∽△ADC;
(3)BC2=2AB·CE.证明:(1)∵AB是⊙O的直径,
∴∠ADB=90°,即AD是底边BC上的高,
又∵AB=AC,
∴△ABC是等腰三角形,∴D是BC的中点; (2)∵∠CBE与∠CAD是 所对的圆周角,∴∠CBE=∠CAD,又∵∠BCE=∠ACD,∴△BEC∽△ADC;
同课章节目录
